概要
ラッチ回路や、フリップフロップ回路は、双安定マルチバイブレータの一種です。
通常、組合せ論理回路は与えられた入力信号に応じた出力がされ、入力信号が無くなると無入力に応じた出力になります。
それに対し、ラッチ回路や、フリップフロップ回路は、入力信号が無くなり、無入力状態になった時は、その直前の出力状態を維持し続けます。
出力状態を維持し続けるということは、直前の状態を記憶することができる回路という事です。その特性を活用して、コンピュータのレジスタ、SRAM等の記憶回路に応用されます。
ラッチ回路は入力信号が変化すると、出力信号が即座に変化します。
この即座に変化するという動作は、ラッチは入力が出力に筒抜けになっているということです。
そのため、予期せぬタイミングで入力が変化すると、出力も一緒に変わってしまうので制御を難しくさせる原因となります。
そのラッチの特性を改善したのがフリップフロップ回路です。
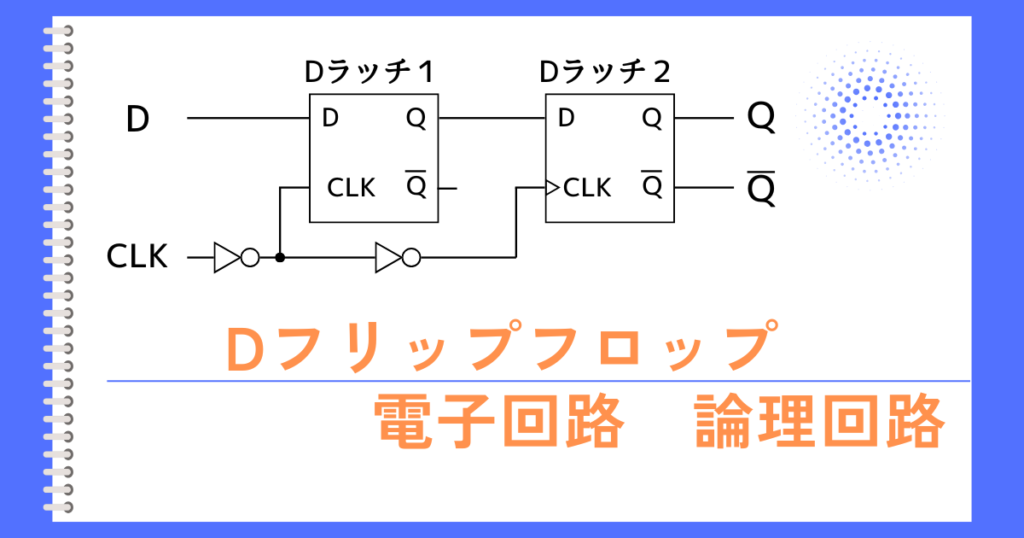
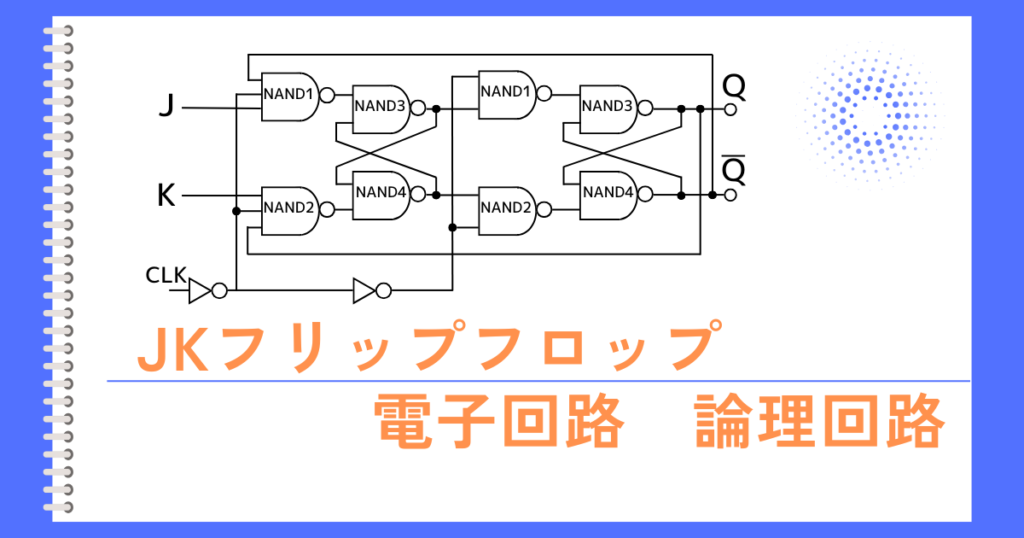
フリップフロップ回路は、クロック信号の立上り、もしくは、立下りのタイミングの瞬間しか出力信号が変化しません。
フリップフロップ回路は、ラッチ回路を組合わせて作られるため、ラッチ回路よりも規模が大きくなってしまうデメリットがあります。
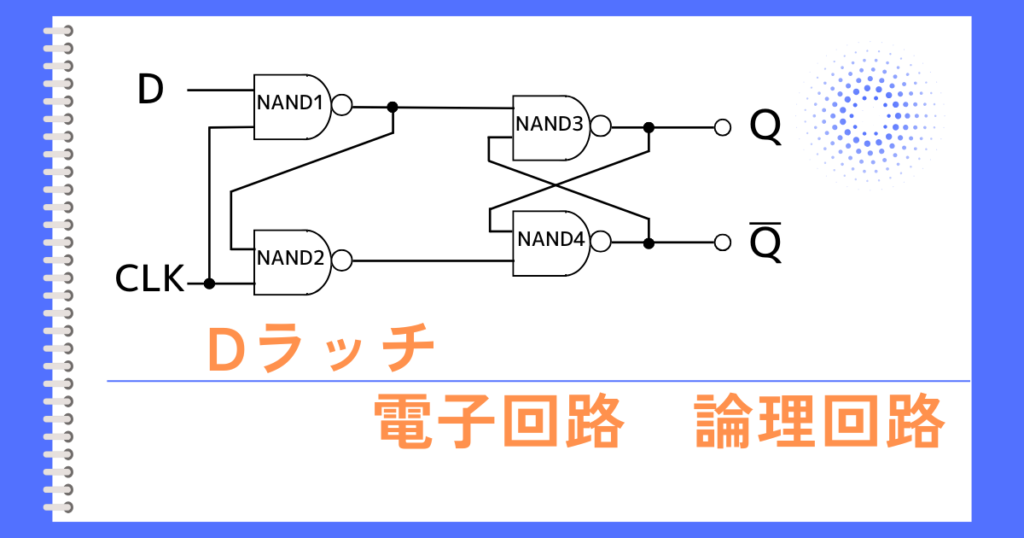
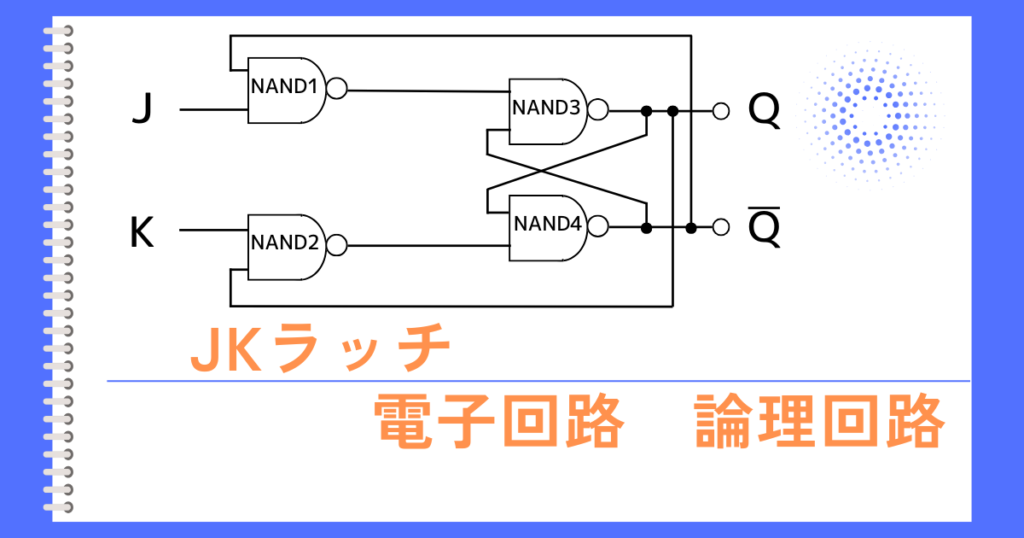
ラッチには、RSラッチ、Dラッチ、JKラッチ、Tラッチ等があります。
これらの中でも、RSラッチは最も基本的な回路です。
その理由は、RSラッチの回路に前段の回路を入れて、RSラッチが禁止状態にならないようにした上で、所定の機能を追加したものが、D、JK、Tラッチであるからです。
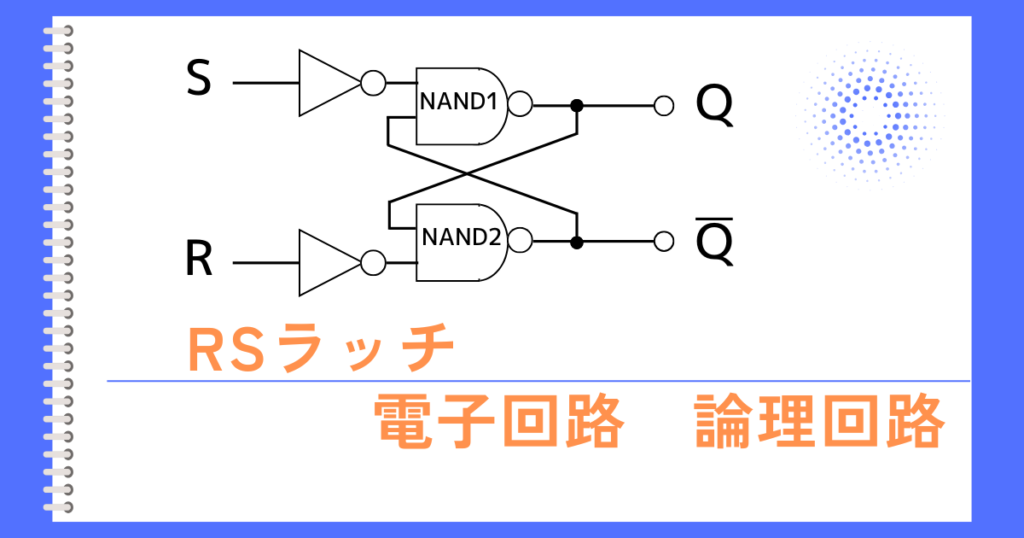
RSラッチ
R(リセット)とS(セット)の2つの信号名からRSラッチと呼びます。
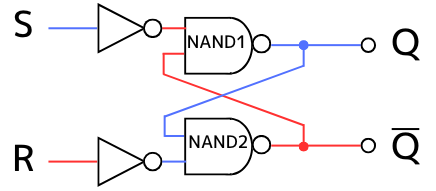
二つのNAND回路の出力を、たすき掛けするように接続したような回路です。
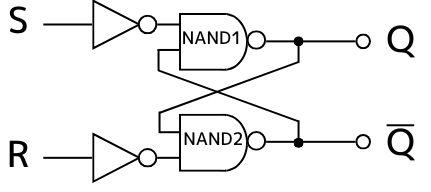
このRSラッチの動作を示す真理値表は、次の通りです。
真理値表
| \(S\) | \(R\) | \(Q\) | \(\overline{Q}\) | 動作解析の説明番号 |
| 0 | 0 | 保持 | 保持 | (1)、(2) |
| 0 | 1 | 0 | 1 | (3)、(4) |
| 1 | 0 | 1 | 0 | (5)、(6) |
| 1 | 1 | 禁止 | 禁止 | (7) |
動作解析

凡例
解析用の回路図は、青線を0、赤線を1とします。
(1)【保持動作】
出力\(Q=1,\overline{Q}=0\)の時に入力\(S=0,R=0\)となった場合
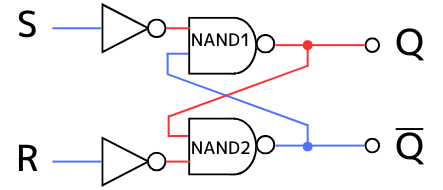
NAND1の入力は1・0 ➔ 出力は\(Q=1\)
NAND2の入力は1・1 ➔ 出力は\(\overline{Q}=0\)
となり、出力は変化しません。
したがって、\(Q=1、\overline{Q}=0\)の時に\(S=0、R=0\)になると、出力が変化しない保持動作をすることが確認できました。
(2)【保持動作】
出力\(Q=0,\overline{Q}=1\)の時に入力\(S=0,R=0\)となった場合
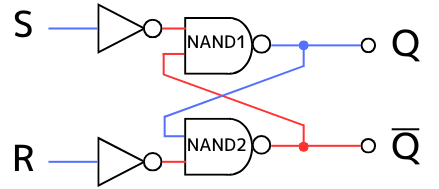
NAND1の入力は1・1 ➔ 出力は\(Q=0\)
NAND2の入力は0・1 ➔ 出力は\(\overline{Q}=1\)
となり、出力は変化しません。
したがって、\(Q=0、\overline{Q}=1\)の時に\(S=0、R=0\)になると、出力が変化しない保持動作をすることが確認できました。
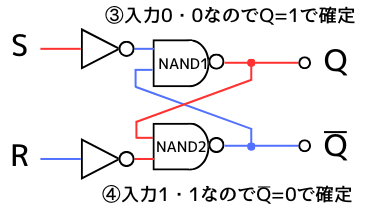
(3)【リセット動作】
出力\(Q=1,\overline{Q}=0\)の時に入力\(S=0,R=1\)となった場合
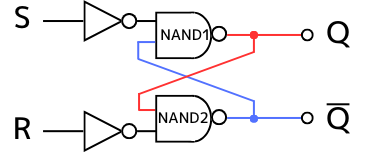
まず初めに出力\(Q=1,\overline{Q}=0\)とします。
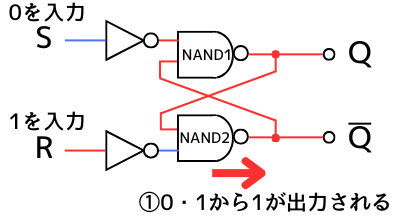
①
入力\(S=0,R=1\)を入力します。このとき、
NAND2の入力は0・1 ➔ 出力は\(\overline{Q}=1\)
となります。
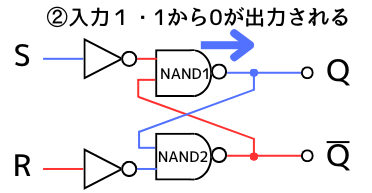
②
NAND1の入力は1・1 ➔ 出力は\(Q=0\)
となります。
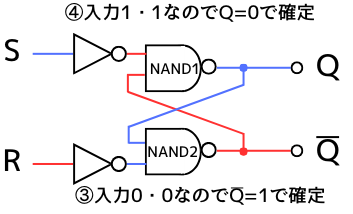
③・④
NAND2の入力は0・0 ➔ 出力は\(\overline{Q}=1\)
NAND1の入力は1・1 ➔ 出力は\(Q=0\)
で安定します。
以上より、\(Q=1、\overline{Q}=0\)の時に\(S=0、R=1\)になると、出力が\(Q=0、\overline{Q}=1\)になるリセット動作をすることが確認できました。
(4)【リセット動作】
出力\(Q=0,\overline{Q}=1\)の時に入力\(S=0,R=1\)となった場合
NAND1の入力は1・1 ➔ 出力は\(Q=0\)
NAND2の入力は0・0 ➔ 出力は\(\overline{Q}=1\)
となり、出力は変化しません。
以上より、\(Q=0、\overline{Q}=1\)の時に\(S=0、R=1\)になると、出力が\(Q=0、\overline{Q}=1\)のリセット状態のままであることが確認できました。
(5)【セット動作】
出力\(Q=1,\overline{Q}=0\)の時に入力\(S=1,R=0\)となった場合
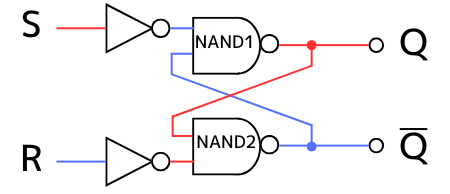
NAND1の入力は0・0 ➔ 出力は\(Q=1\)
NAND2の入力は1・1 ➔ 出力は\(\overline{Q}=0\)
となり、出力は変化しません。
以上より、\(Q=1、\overline{Q}=0\)の時に\(S=1、R=0\)になると、出力が\(Q=1、\overline{Q}=0\)のセット状態のままであることが確認できました。
(6)【セット動作】
出力\(Q=0,\overline{Q}=1\)の時に入力\(S=1,R=0\)となった場合
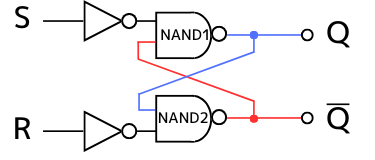
まず初めに出力\(Q=0,\overline{Q}=1\)とします。
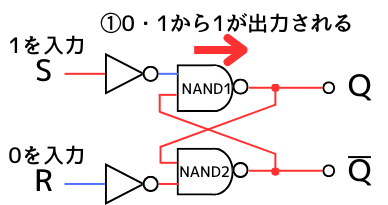
①
入力\(S=1,R=0\)を入力します。このとき、
NAND1の入力は0・1 ➔ 出力は\(Q=1\)
となります。
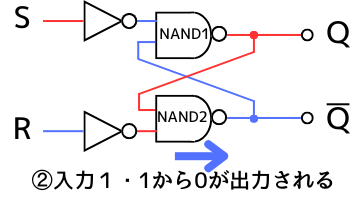
②
NAND2の入力は1・1 ➔ 出力は\(\overline{Q}=0\)
となります。
③・④
NAND1の入力は0・0 ➔ 出力は\(Q=1\)
NAND2の入力は1・1 ➔ 出力は\(\overline{Q}=0\)
で安定します。
以上より、\(Q=0、\overline{Q}=1\)の時に\(S=1、R=0\)になると、出力が\(Q=1、\overline{Q}=0\)になるセット動作をすることが確認できました。
(7)【禁止動作】
\(S=1,R=1\)が禁止の理由
\(S=1,R=1\)の時、\(Q=1,\overline{Q}=1\)状態となります。
この状態から、保持状態\(S=0,R=0\)に切り替えようとしたときを考えます。
入力信号を2つ切り替えるので、そのタイミングによって次の3つの状態のどれかになります。
①\(S=0\)となった後に\(R=0\)になる
⇒セット状態が保持される。(\(Q=1,\overline{Q}=0\))
②\(R=0\)となった後に\(S=0\)になる
⇒リセット状態が保持される。(\(Q=0,\overline{Q}=1\))
③完全に同時のタイミングで\(S=0,R=0\)になる
⇒(\(Q=1,\overline{Q}=1\))と、(\(Q=0,\overline{Q}=0\))の状態を繰り返します。
NANDゲートの遅延の個体差によって出力状態が崩れるまで繰り返します。
つまり、
\(S=1,R=1\)としてしまうと、\(S=0,R=0\)になった時に何が保持されるかわからず、不確定になってしまう問題があるため、\(S=1,R=1\)は禁止とされています。
関連記事(その他)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント