概要
直線状導体と、円形コイルの磁界の強さが等しくなる電流を求める計算問題です。
円形コイルの磁界の強さの導出は、導出工程が多く手間なので、公式を記憶出来ていると良いかもしれません。
キーワード
直線状導体、円形コイル、アンペールの法則、ビオサバールの法則、磁界の強さ
問題
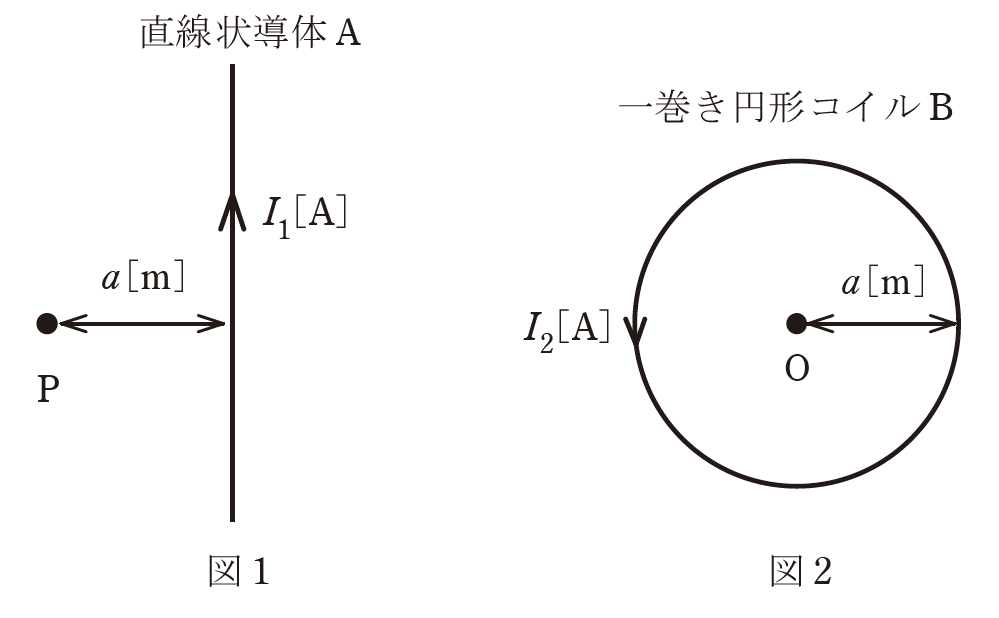
図 1 のように、無限に長い直線状導体 A に直流電流 \(I_1[A]\)が流れているとき、この導体から\(a[m]\)離れた点P での磁界の大きさは\(H_1 [A/m]\)であった。
一方、図 2のように半径\(a[m]\)の一巻きの円形コイルB に直流電流\(I_2 [A]\)が流れているとき、この円の中心点O での磁界の大きさは\(H_2 [A/m]\)であった。
\(H_1=H_2\) であるときの\(I_1\)と\(I_2\)の関係を表す式として正しいものを、次の(1)~(5)のうちから一つ選べ。
(1)\(I_1=π^2I_2\) (2)\(I_1=\frac{2}{π}I_2\) (3)\(I_1=\frac{I_2}{π^2}\)
(4)\(I_1=\frac{I_2}{π}\) (5)\(I_1=πI_2\)
答え
(5)
解説テキスト リンク
回答解説
回答の流れ
1. 直線状導体Aが点Pに作る磁界の強さ\(H_1\)を求める
2. 一巻円形コイルBが中心点Oに作る磁界の強さ\(H_2\)を求める
3. \(H_1=H_2\)から電流\(I_1\)を求める
1. 直線状導体Aが点Pに作る磁界の強さ\(H_1\)を求める
直線状導体Aに直流電流 \(I_1[A]\)が流れているとき、この導体から\(a[m]\)離れた点P の磁界の大きさ\(H_1 [A/m]\)は、アンペールの法則から、
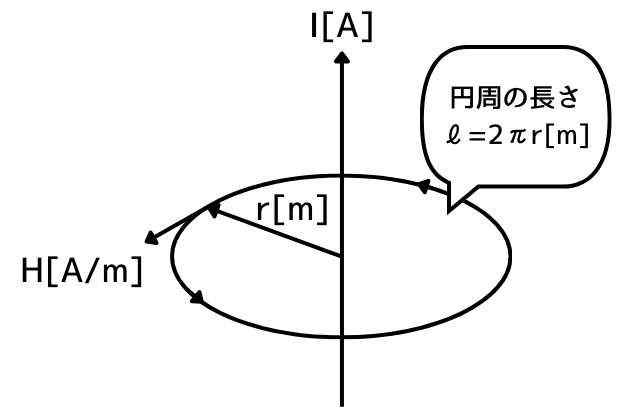
\( \displaystyle I_1=\oint_C H_1dl=H_1l=H_1× 2π a \)
となります。変形すると、
\(\displaystyle H_1=\frac{I}{2πa}[A/m]\)
となります。
2. 一巻円形コイルBが中心点Oに作る磁界の強さ\(H_2\)を求める
半径\(a[m]\)の一巻きの円形コイルB に直流電流\(I_2 [A]\)が流れているとき、この円の中心点O での磁界の大きさ\(H_2 [A/m]\)は、ビオサバールの法則から、
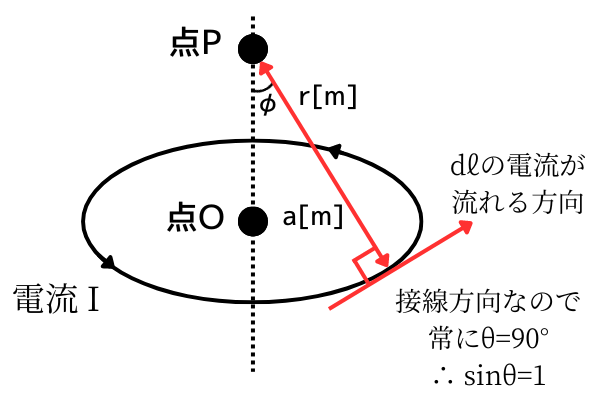
中心軸上の任意の点を点Pとしたとき、微小区間\(dl\)の電流が流れた時の点Pの磁界の強さ\(H\)は、
\(\displaystyle dH=\frac{Idl}{4π r^2}・sinθ\)
\(θ=90°\)から\(sinθ=1\)なので、
\(\displaystyle dH=\frac{Idl}{4π r^2}\) …①
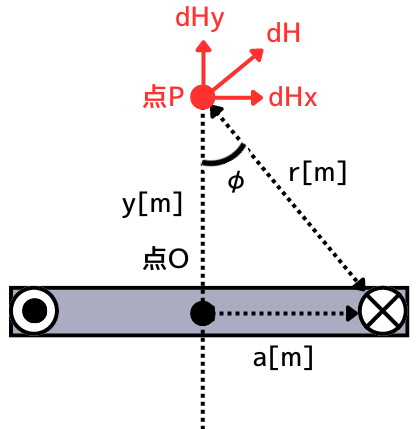
円形電線を横から見たとき、\(dl\)が作る磁界\(dH\)は、\(dH_x\)、\(dH_y\)と分解できます。
円形電線は、点Pの周りを1周するため、\(dH_x\)のベクトル和は\(0\)になります。
したがって、\(dH_y\)のみが残りますので、
\(dH_y=dH sinφ\) ………②
②式に①式を代入すると、
\( dH_y=\frac{Idl}{4π r^2}・sinφ\) …③
となります。③式を積分すると、
\(\begin{eqnarray} H_y&=&\int_0^{2π a}\frac{I}{4π r^2}・sinφ dl \\
&=&\frac{I}{4π r^2}・sinφ\int_0^{2π a} dl \\
&=&\frac{I}{4π r^2}・sinφ・2π a …④
\end{eqnarray}\)
となります。ここで、
\(\displaystyle sinφ=\frac{a}{r}\) …⑤
なので、⑤式を④式に代入すると、
\(H_y=\frac{Ia^2}{2 r^3}\) …⑥
となります。ここで、
\(r=\sqrt{a^2+y^2}\) …⑦
なので、⑦式を⑥式に代入すると、
\(\displaystyle H_y=\frac{Ia^2}{2 (a^2+y^2)^{\frac{3}{2}}}\) …⑧
\(y=0\)のとき、点Oの磁界の強さ\(H_2\)になるので、
\(\displaystyle H_2=\frac{Ia^2}{2 (a^2)^{\frac{3}{2}}}=\frac{I}{2a}\) …⑨
以上より、点Oにつくる磁界の強さ\(H_2\)は、
\(H_2=\frac{I}{2a}\)
と、求まりました。
3. \(H_1=H_2\)から電流\(I_1\)を求める
問題文の条件、\(H_1=H_2\)なので、
\(\frac{I_1}{2πa}=\frac{I_2}{2a}\)
⇔ \(I_1=πI_2\)
以上より、(5)\(I_1=πI_2\)が答えです。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和7年度上期 第三種電気主任技術者試験 理論科目問4
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。






コメント