概要
電気計測の計算問題です。
その実は、条件に応じた直流電圧・直流電流・合成抵抗の計算問題です。
問題文中に示された条件を、しっかりと読み込んで計算していけば簡単な問題です。
キーワード
電気計測、キルヒホッフの法則、オームの法則、合成抵抗
問題
次に示す条件Ⅰ~Ⅲを満たす永久磁石可動コイル形電流電圧計を製作したい。
永久磁石可動コイル形電流電圧計内部の接続の一部が図に示すようであるとき、次の(a)及び(b)の問に答えよ。
ただし、コイルは内部抵抗\(r=5Ω\) であり、最大 \(4 mA\) まで直流電流を流すことができるものとする。
条件Ⅰ:切り替えスイッチをA にしたときは、最大\(1A\) の直流電流を測定できるものとする。
条件Ⅱ:切り替えスイッチをB にしたときは、最大\(100 mA\) の直流電流を測定できるものとする。
条件Ⅲ:切り替えスイッチをC にしたときは、最大\(1.2 V\) の直流電圧を測定できるものとする。
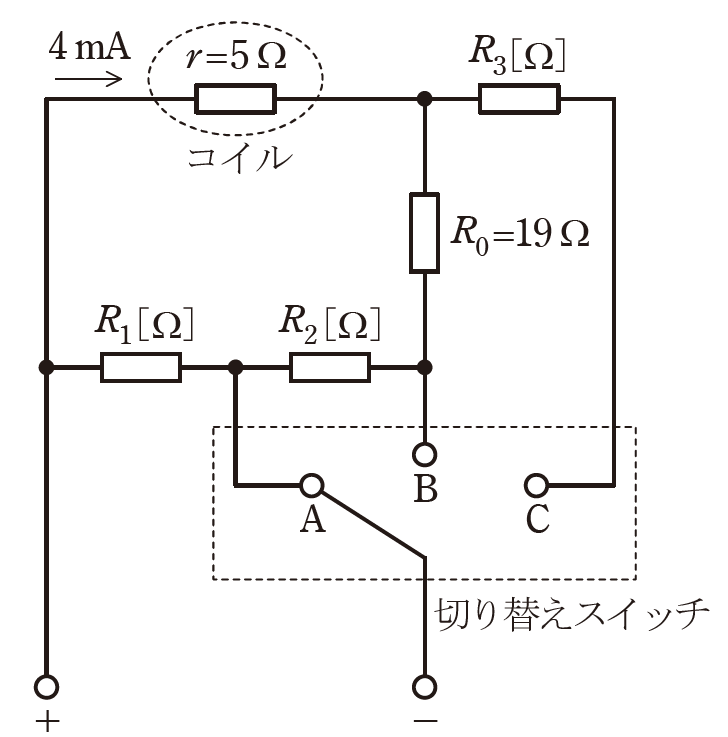
(a) 抵抗\(R_1\) の値\([Ω]\)として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)0.1 (2)0.9 (3)4 (4)9.6 (5)9.96
(b) 抵抗\(R_3\) の値\([Ω]\)として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)2.36 (2)23.6 (3)25 (4)236 (5)2360
答え
(a)(1)
(b)(4)
解説テキスト リンク
回答解説
(a)問題
回答の流れ
1.条件Ⅰから\(R_1\)と\(R_2\)の関係を導出
2.条件Ⅱから\(R_1\)を導出
1.条件Ⅰから\(R_1\)と\(R_2\)の関係を導出
電流電圧計の端子間電圧を\(V[V]\)とします。
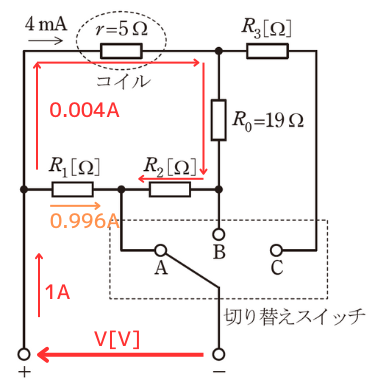
条件Ⅰから、次の2式が成り立ちます。
・\(V=0.004(r+R_0+R_2)=0.096+0.004R_2\) …①
・\(V=0.996R_1\) …②
①=②なので、
\(R_2=249R_1-24\) …③
2.条件Ⅱから\(R_1\)を導出
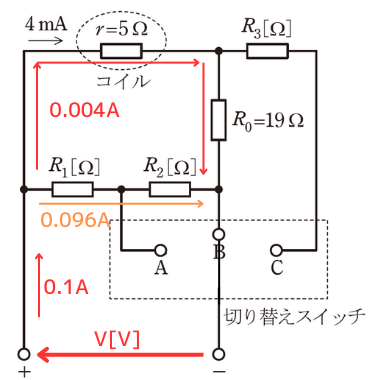
条件Ⅱから、次の2式が成り立ちます。
・\(V=0.004(r+R_0)=0.004(5+19)=0.096\) …④
・\(V=R_1+R_2=250R_1-24\) …⑤
④=⑤なので、
\(R_1=\frac{0.096+24}{250}=0.096384≒0.1Ω\)
以上より、(a)問題は(1)\(0.1Ω\) が答えです。
(b)問題
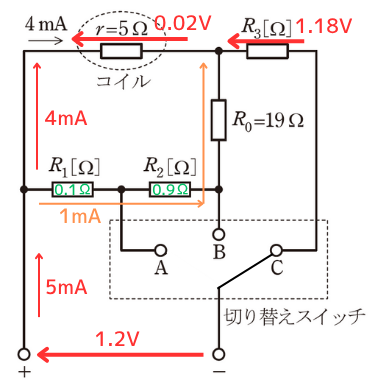
条件Ⅲから、次の2式が成り立ちます。
コイルの両端の電位差は、
\(V_r=0.004・5=0.02\) …⑥
\(R_1\)、\(R_2\)、\(R_0\)の合成抵抗\(R’\)は、
\(R’=R_1+R_2+R_0=0.1+0.9+19=20Ω\) …⑦
合成抵抗に流れる電流\(I’\)は、⑥・⑦式から、
\(I’=\frac{V_r}{R’}=\frac{0.02}{20}=1mA\) …⑧
電圧計の端子に流れる電流\(I\)は、コイルに流れる4mAと、\(I’\)の合計なので、
\(I=4+I’=4+1=5mA\) …⑨
抵抗\(R_3\)の端子間電圧\(V_{R3}\)は、
\(V_{R3}=1.2-0.02=1.18V\) …⑩
抵抗\(R_3\)は、⑨・⑩式から、
\(R_3=\frac{V_{R3}}{I}=\frac{1.18}{5×10^{-3}}=236Ω\)
以上より、(b)問題は(4)\(236Ω\) が答えです。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和7年度上期 第三種電気主任技術者試験 理論科目問16
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。






コメント