概要
量と単位の紐づけの問題です。
単位の関連性を一々覚えておくことは非常に非効率的なので、関連式から単位を導き出せるようになると、この手の問題は回答できるようになります。
キーワード
単位
問題
電気及び磁気に関する量とその単位記号(これと同じ内容を表す単位記号を含む。)の組み合わせとして、誤っているのは次のうちどれか。
| 量 | 単位記号 | |
|---|---|---|
| (1) | 電流 | \(C/s\) |
| (2) | 磁気抵抗 | \(H^{-1}\) |
| (3) | 電力量 | \(W・s\) |
| (4) | 磁束 | \(T\) |
| (5) | 電界の強さ | \(V/m\) |
答え
(4)
解説テキスト リンク
回答解説
(1)電流:\(C/s\)
電流\(I[A]\)の定義は、単位時間あたりに通過する電荷量\(Q[C]\)です。
式で示すと、
\(I[A]=\frac{Q[C]}{t[s]}\)
したがって、(1)電流\(C/s\) は正しいです。
(2)磁気抵抗:\(H^{-1}\)
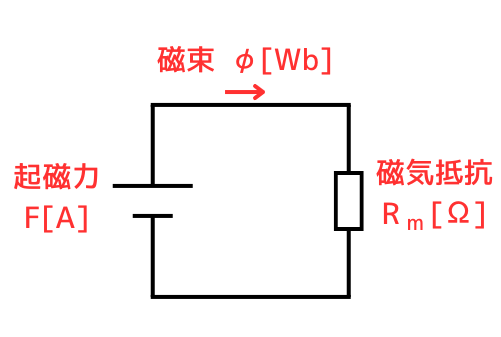
起磁力\(F[A]\)、磁束\(\phi[Wb]\)、磁気抵抗\(R_m\)としたとき、
磁気回路のオームの法則から、
\(F=\phi R_m\)
⇔\(\displaystyle R_m=\frac{F[A]}{\phi[Wb]}\) …①
起磁力\(F[A]\)は、コイルの巻数\(N\)[回]、コイルに流れる電流\(I[A]\)としたとき、次式で表されます。
\(F=NI\) …②
磁束\(\phi[Wb]\)は、コイルの巻数\(N\)[回]、コイルに流れる電流\(I[A]\)、コイルの自己インダクタンス\(L[H]\)としたとき、
\(N\phi=LI\)
⇔\(\displaystyle \phi=\frac{LI}{N}\) …③
①式に、②・③式を代入すると、
⇔\(\displaystyle R_m=\frac{NI}{\frac{LI}{N}}=\frac{N^2}{L}\)
コイルの巻数\(N\)[回]は、無次元なので、磁気抵抗の単位は\([H^{-1}]\)であることがわかります。
したがって、(2)磁気抵抗:\(H^{-1}\) は正しいです。
(3)電力量:\(W・s\)
電力量は、ある時間内に消費された電力の総量の事です。
1秒あたりに消費される電気エネルギーの量を表す単位\([W]\)に、時間\([s]\)を掛けたものが電力量になります。
したがって、(3)電力量:\(W・s\) は正しいです。
(4)磁束:\(T\)
磁束\(Φ\)の単位は\([Wb]\)です。
単位\([T]\)は、磁束密度の単位です。
磁束\(Φ[Wb]\)と磁束密度\(B[T]\)の関係は、面積を\(S[m^2]\)としたとき、
\(Φ=BS\)と表されます。
このことから、
\([Wb]=[T・m^2]\)
⇔\([T]=\frac{[Wb]}{[m^2]}=[Wb/m^2]\)
の関係があります。
したがって、(4)磁束:\(T\) が誤りです。
(5)電界の強さ:\(V/m\)
極板間距離\(d[m]\)のコンデンサに電位\(V[V]\)を与えた時の電界の強さ\(E[V/m]\)は、
\(\displaystyle E=\frac{V[V]}{d[m]}\)です。
したがって、(5)電界の強さ:\(V/m\) は正しいです。
以上より、(4)が答えです。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和7年度上期 第三種電気主任技術者試験 理論科目問14
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。






コメント