概要
コンデンサの電極間の等電位分布を求める問題です。
物理的な意味を理解していれば、求めるべき物は単純です。
しかし、等電位分布という名前で直接示す公式は存在しないので案外詰まりやすいかもしれない問題です。
キーワード
電界、等電位分布
問題
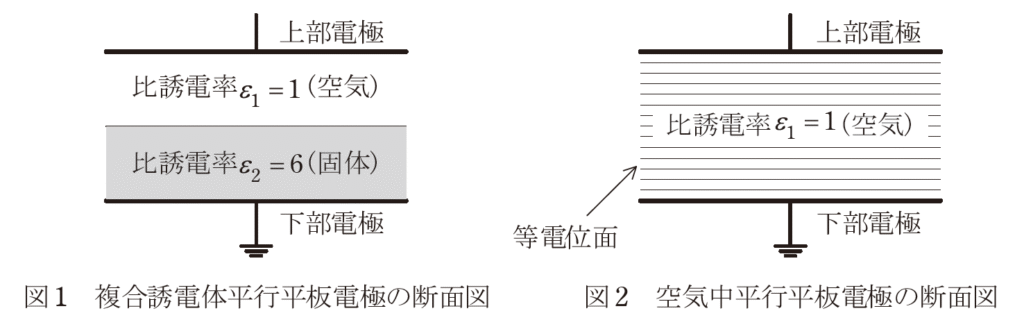
図1に示すような、空気を含む二つの誘電体からなる平行平板電極がある。
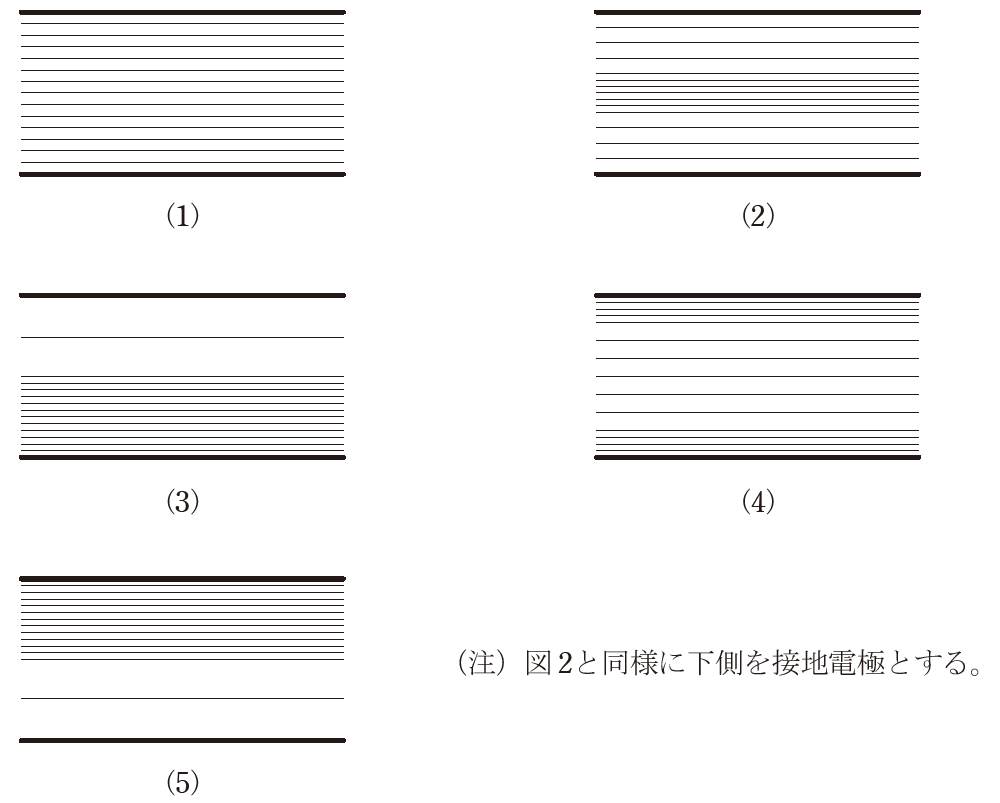
この下部電極を接地し、上部電極に電圧を加えたときの電極間の等電位線の分布を示す断面図として、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、誘電体の導電性及び電極と誘電体の端効果は無視できるものとする。
参考までに固体誘電体を取り除いた、空気中平行平板電極の場合の等電位線の分布を図2に示す。
答え
(5)
解説テキスト リンク
回答解説
回答の流れ
(1) 電界強度\(E[V/m]\)を求める
(1) 電界強度\(E[V/m]\)を求める
電界強度\(E[V/m]\)は、電位の傾きです。
等電位線は、山の等高線のように、傾きが大きい所では間隔が狭くなり、傾きが小さい所では間隔が広くなります。このことから、
電界強度\(E[V/m]\)が大きい ➡ 電位の傾きが大きい ➡ 等電位線の分布は狭い
電界強度\(E[V/m]\)が小さい ➡ 電位の傾きが小さい ➡ 等電位線の分布は広い
この事を理解していれば、電界強度を求めるだけで等電位線の分布が求められることがわかります。
電界強度の式は、\(E=\frac{Q}{ε_rε_0S}\)です。
※\(ε_r\):比誘電率、\(ε_0\):真空の電率、\(S\):極板面積、\(Q\):電荷量
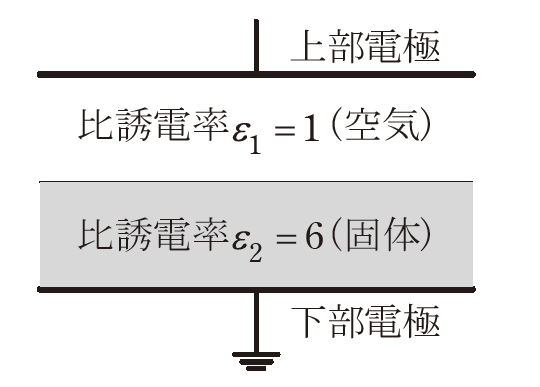
空気の電界強度\(E_1\)は、
\(E_1=\frac{Q}{ε_1ε_0S}=\frac{Q}{ε_0S}\)
固体の電界強度\(E_2\)は、
\(E_2=\frac{Q}{ε_2ε_0S}=\frac{Q}{6ε_0S}=\frac{1}{6}E_1\)
以上の情報をまとめると、電界強度\(E_1\)の方が\(E_2\)よりも大きいため、等電位分布は狭くなります。
したがって、(5)が答えです。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和6年度上期 第三種電気主任技術者試験 理論科目A問題問1
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント