概要
RLC直列回路の知識を問う論説問題です。
共振時のインピーダンス、周波数を下げたとき、上げたときの位相特性に関する知識が問われます。
知識として知っていなかったり、忘れてしまっていても、計算すれば簡単に回答が出ますので、諦めずに計算しましょう。
キーワード
交流回路、RLC直列回路、共振、誘導性リアクタンス、容量性リアクタンス、位相特性
問題
次の文章は、RLC直列共振回路に関する記述である。
\(R[Ω]\)の抵抗、インダクタンス\(L[H]\)のコイル、静電容量\(C[F]\)のコンデンサを直列に接続した回路がある。
この回路に交流電圧を加え、その周波数を変化させると、特定の周波数\(f_r[Hz]\)のときに誘導性リアクタンス\(2πf_rL[Ω]\)と容量性リアクタンス\(\frac{1}{2πf_rC}[Ω]\)の大きさが等しくなり、その作用が互いに打ち消し合って回路のインピーダンスが ア なり、 イ 電流が流れるようになる
この現象を直列共振といい、このときの周波数\(f_r[Hz]\)をその回路の共振周波数という。
回路のリアクタンスは共振周波数\(f_r[Hz]\)より低い周波数では ウ となり、電圧より位相が エ 電流が流れる。
また、共振周波数\(f_r[Hz]\)より高い周波数では オ となり、電圧より位相が カ 電流が流れる。
上記の記述中の空白箇所(ア)~(カ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | (オ) | (カ) | |
| (1) | 大きく | 小さな | 容量性 | 進んだ | 誘導性 | 遅れた |
| (2) | 小さく | 大きな | 誘導性 | 遅れた | 容量性 | 進んだ |
| (3) | 小さく | 大きな | 容量性 | 進んだ | 誘導性 | 遅れた |
| (4) | 大きく | 小さな | 誘導性 | 遅れた | 容量性 | 進んだ |
| (5) | 小さく | 大きな | 容量性 | 遅れた | 誘導性 | 進んだ |
答え
(3)
解説テキスト リンク
関連箇所直リンク
・RLC直列回路
回答解説
回答の流れ
(a)共振時のインピーダンス
①共振時のインピーダンスを計算する
②共振時の電流を計算する
(b)周波数が低いとき
③非常に低い周波数\(f_L[Hz]\)のときのインピーダンスを求める
④\(f_L[Hz]\)の時のインピーダンスの位相を求める
⑤\(f_L[Hz]\)の時の電流の位相を求める
(c)周波数が高いとき
⑥非常に高い周波数\(f_H[Hz]\)のときのインピーダンスを求める
⑦\(f_H[Hz]\)の時のインピーダンスの位相を求める
⑧\(f_H[Hz]\)の時の電流の位相を求める
(a)共振時のインピーダンス
①共振時のインピーダンスを計算する
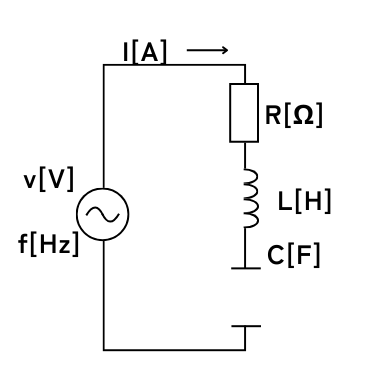
RLC直列回路のインピーダンス\(Z\)は
\(\displaystyle Z=R+j2πfL+\frac{1}{j2πfC}\)
⇔ \(\displaystyle Z=R+j \left( 2πfL-\frac{1}{2πfC} \right) \)
共振周波数\(f_r[Hz]\)のとき、
\(\displaystyle 2πf_rL-\frac{1}{2πf_rC}=0 \)
となり、この時のインピーダンス\(Z\)は、
\(Z=R\)
共振周波数以外の周波数\(f[Hz]\)の時のインピーダンスの大きさは
\(\displaystyle Z=\sqrt{R^2+\left( 2πfL-\frac{1}{2πfC} \right)^2}\)
なので、共振時のインピーダンスは全周波数のインピーダンスの中で最小です。
したがって、回路のインピーダンスは ア=小さく なります。
②共振時の電流を計算する
共振時、回路に流れる電流\(I[A]\)は、
\(\displaystyle I=\frac{v}{Z}=\frac{v}{R}\)
となり、 イ=大きな 電流が流れます。
(b)周波数が低いとき
③低い周波数\(f_L[Hz]\)のときのインピーダンスを求める
インピーダンスの式 \(\displaystyle Z=R+j \left( 2πfL-\frac{1}{2πfC} \right) \)
から、周波数が\(f_r[Hz]\)よりも低い\(f_L[Hz]\)になると、
・誘導性リアクタンス\(2πfL\)は比例して小さくなります。
・容量性リアクタンス\(\displaystyle \frac{1}{2πfC}\)は反比例して大きくなります。
したがって、容量性リアクタンスの影響が大きくなるため、回路のリアクタンスは ウ=容量性 となります。
④\(f_L[Hz]\)の時のインピーダンスの位相を求める
周波数\(f_L[Hz]\)が非常に低く、誘導性リアクタンスが無視できるとしたときのインピーダンス\(Z_L\)は、次式となります。
\(\displaystyle Z_L=R-j\frac{1}{2πfC} \)
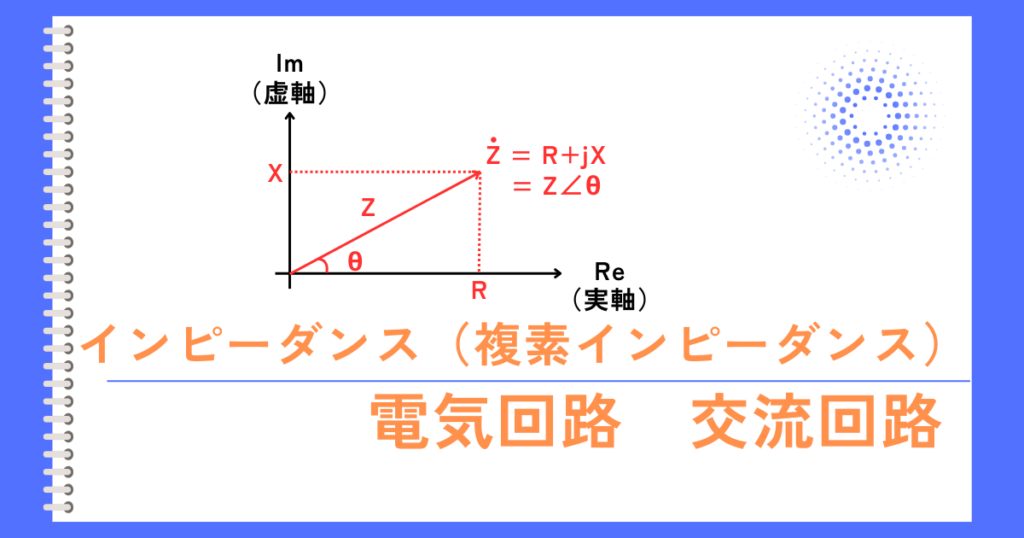
\(Z_L\)の位相角\(∠θ_{ZL}\)は、
\(\displaystyle ∠θ_{ZL}=tan^{-1}\frac{Im}{Re}=tan^{-1}\frac{-\frac{1}{2πfC}}{R}=tan^{-1}\frac{-1}{2πfCR}\)
⑤\(f_L[Hz]\)の時の電流の位相を求める
電圧の位相\(∠θ_v=0°\)としたときの電流の位相\(∠θ_I\)は、
\(\displaystyle ∠θ_I=\frac{∠θ_v}{∠θ_{ZL}}=\frac{0°}{-tan^{-1}\frac{1}{2πfCR}}\)
⇔ \(\displaystyle ∠θ_I=0- \left( -tan^{-1}\frac{1}{2πfCR}\right) \)
⇔ \(\displaystyle ∠θ_I=tan^{-1}\frac{1}{2πfCR}\)
以上より、電流の位相\(∠θ_I\)はプラスであるため、電圧の位相\(∠θ_v\)より位相が エ=進んだ 電流が流れます。
(c)周波数が高いとき
⑥非常に高い周波数\(f_H[Hz]\)のときのインピーダンスを求める
インピーダンスの式 \(\displaystyle Z=R+j \left( 2πfL-\frac{1}{2πfC} \right) \)
から、周波数が\(f_r[Hz]\)よりも高い\(f_H[Hz]\)になると、
・誘導性リアクタンス\(2πfL\)は比例して大きくなります。
・容量性リアクタンス\(\displaystyle \frac{1}{2πfC}\)は反比例して小さくなります。
したがって、誘導性リアクタンスの影響が大きくなるため、回路のリアクタンスは オ=誘導性 となります。
⑦\(f_H[Hz]\)の時のインピーダンスの位相を求める
周波数\(f_H[Hz]\)が非常に高く、容量性リアクタンスが無視できるとしたときのインピーダンス\(Z_H\)は、次式となります。
\(\displaystyle Z_H=R+j2πfL \)
\(Z_H\)の位相角\(∠θ_{ZH}\)は、
\(\displaystyle ∠θ_{ZH}=tan^{-1}\frac{Im}{Re}=tan^{-1}\frac{2πfL}{R}\)
⑧\(f_H[Hz]\)の時の電流の位相を求める
電圧の位相\(∠θ_v=0°\)としたときの電流の位相\(∠θ_I\)は、
\(\displaystyle ∠θ_I=\frac{∠θ_v}{∠θ_{ZH}}=\frac{0°}{tan^{-1}\frac{2πfL}{R}}\)
⇔ \(\displaystyle ∠θ_I=0- \left( tan^{-1}\frac{2πfL}{R} \right) \)
⇔ \(\displaystyle ∠θ_I=-tan^{-1}\frac{2πfL}{R}\)
以上より、電流の位相\(∠θ_I\)はマイナスであるため、電圧の位相\(∠θ_v\)より位相が カ=遅れた 電流が流れます。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和5年度上期 第三種電気主任技術者試験 理論科目A問題問8
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント