概要
ホール素子に関する論説問題です。
ホール素子がフレミング左手の法則の向きに、キャリアにローレンツ力が働くことを理解している必要があります。向きさえ分かれば選択肢が絞れるので、問題としては普通程度の難易度です。
最後の(エ)の内容を理解するには、電験三種でカバーすべき範囲を大きく超えているので、二種を目指す人以外は完答を目指す必要性は薄いです。
キーワード
ホール素子、ホール効果、フレミング左手の法則、ローレンツ力
問題
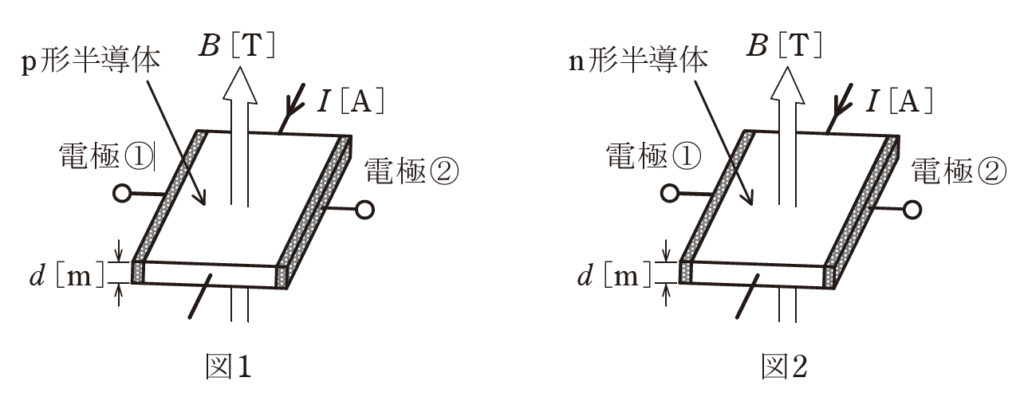
次の文章は、図1及び図2に示す原理図を用いてホール素子の動作原理について述べたものである。
図1に示すように、p形半導体に直流電流\(I[A]\)を流し、半導体の表面に対して垂直に下から上向きに磁束密度\(B[T]\)の平等磁界を半導体にかけると、半導体内の正孔は進路を曲げられ、電極①には \(\fbox{ (ア) }\)電荷、電極②には \(\fbox{ (イ) }\)電荷が分布し、半導体の内部に電界が生じる。
また、図2のn形半導体の場合は、電界の方向はp形半導体の方向と \(\fbox{ (ウ) }\)である。
この電界により、電極①-②間にホール電圧\(V_H=R_H×\fbox{ (エ) }[V]\)が発生する。
ただし、\(d[m]\)は半導体の厚さを示し、\(R_H\)は比例定数\([m^3/C]\)である。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
|---|---|---|---|---|
| (1) | 負 | 正 | 同じ | \(\displaystyle \frac{B}{Id}\) |
| (2) | 負 | 正 | 同じ | \(\displaystyle \frac{Id}{B}\) |
| (3) | 正 | 負 | 同じ | \(\displaystyle \frac{d}{BI}\) |
| (4) | 負 | 正 | 反対 | \(\displaystyle \frac{BI}{d}\) |
| (5) | 正 | 負 | 反対 | \(\displaystyle \frac{BI}{d}\) |
答え
(4)
解説テキスト リンク
回答解説
ホール素子の動作原理
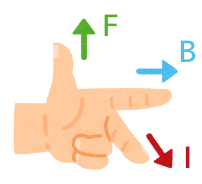
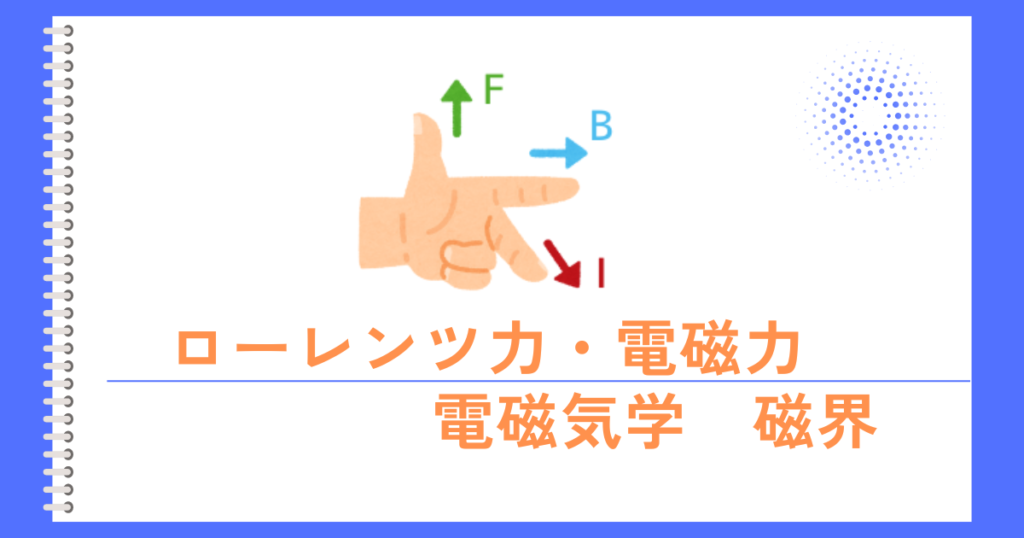
フレミング左手の法則は
・親指:電磁力(F[N]\)
・人差し指:磁界\(B[T]\)
・中指:電流\(I[A]\)
の向きを表します。
ホール素子はホール効果を動作原理とした素子です。
電流を形成するキャリア(正孔・電子)は、ローレンツ力を受けて移動します。移動する向きはフレミング左手の法則の親指の向きです。
それにより、物質の端にキャリアが集まることで、起電力が発生する現象がホール効果です。
電極①には \(\fbox{ (ア) }\)電荷、電極②には \(\fbox{ (イ) }\)電荷が分布し、半導体の内部に電界が生じる。
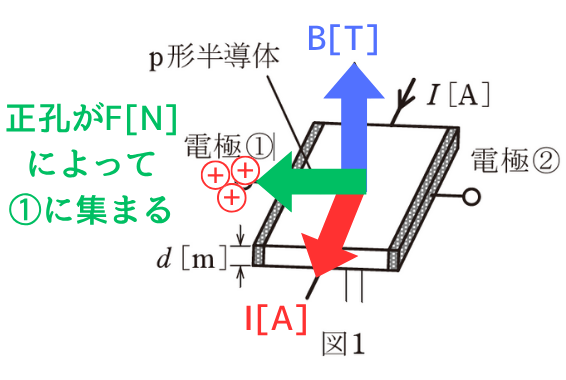
p型半導体のキャリアは正孔(正電荷)です。
フレミング左手の法則の親指の向きにローレンツ力が働き、正孔が電極①に集まります。
その結果、電極①に正電荷が分布します。
対極である電極②には負電荷が分布します。
したがって、\(\fbox{(ア)}\)は正電荷
\(\fbox{(イ)}\)は負電荷です。
図2のn形半導体の場合は、電界の方向はp形半導体の方向と \(\fbox{ (ウ) }\)である。
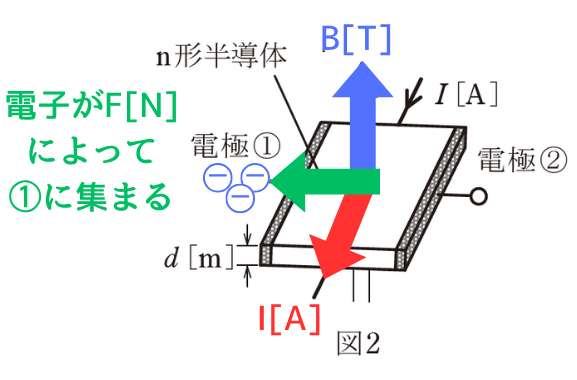
n型半導体のキャリアは電子(負電荷)です。
フレミング左手の法則の親指の向きにローレンツ力が働き、電子が電極①に集まります。
その結果、電極①に負電荷が分布します。
対極である電極②には正電荷が分布します。
p型は①(正) ⇨ ②(負)の向きに電界が発生します。
n型は①(負) ⇦ ②(正)の向きに電界が発生します。
したがって、\(\fbox{(ウ)}\)は反対です。
この電界により、電極①-②間にホール電圧\(V_H=R_H×\fbox{ (エ) }[V]\)が発生する。
電位が発生する原理の解析から、\(V_H=R_H×\fbox{(エ)}[V]\)は\(\displaystyle V_H=R_H\frac{IB}{d}\)です。
以上より、(4)が答えです。
電位が発生する原理の解析
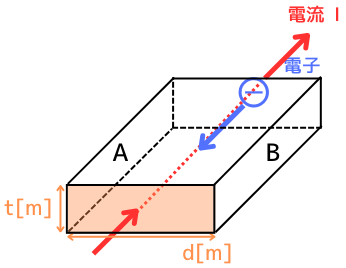
磁界を加えられていないとき
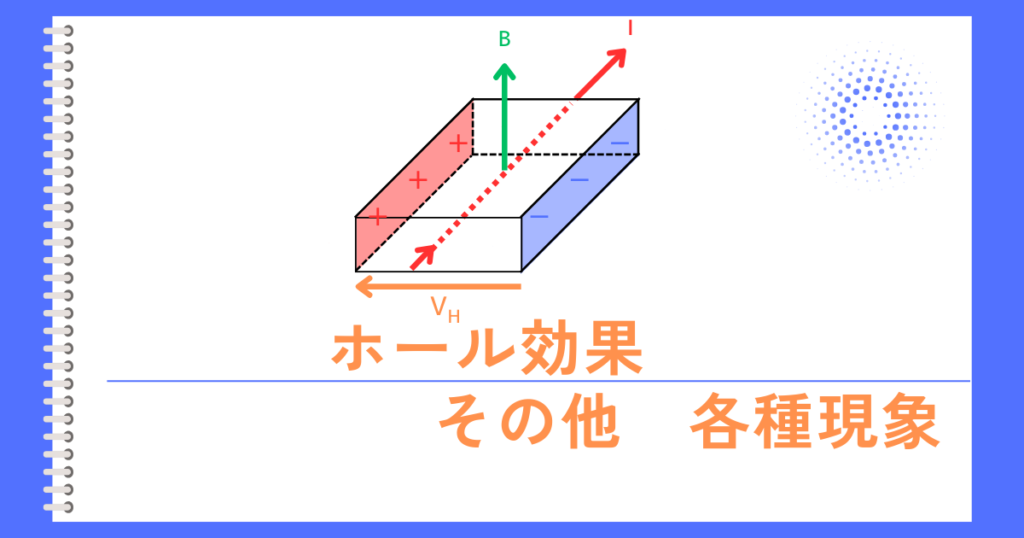
左図のような直方体で、電子がキャリアのN型半導体について考えていきます。
磁界が加えられていないとき、電流\(I[A]\)が流れていても、A面・B面にはキャリアの偏りがないため、電位は発生しません。
流れている電流\(I[A]\)は、電子の電気素量\(e[C]\)、電子の密度\(n\)[個/\(m^3\)]、電子の速度\(v[m/s]\)、物質の厚さ\(t[m]\)、幅\(d[m]\)としたとき、次のように表されます。
\(I=envtd\) …(1)
変形すると、
\(\displaystyle v=\frac{I}{entd}\) …(2)
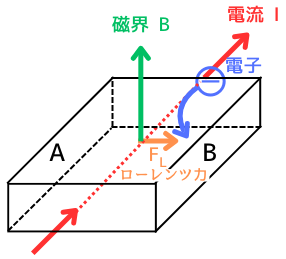
磁束密度\(B[T]\)の磁界を加える
磁束密度\(B[T]\)の磁界を加えると、フレミング左手の法則に従って、電子にローレンツ力\(F_L[N]\)が働いてB面に引き寄せます。
\(F_L=evB\) …(3)
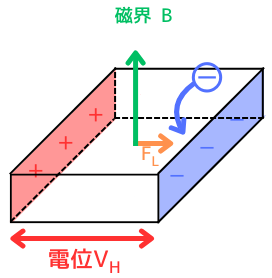
電位\(V_H[V]\)が発生する
キャリアの密度が偏ることによって、A面・B面間に電位\(V_H\)が発生します。
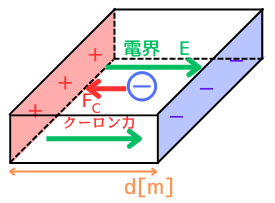
電界強度\(E[V/m]\)の電界が発生する
発生した電位は、A面・B面間に電界強度\(E[V/m]\)の一様な電界を発生させます。
一様な電界における電位\(V_H\)と電界\(E\)の関係は、物質の幅\(d\)を使うと、コンデンサと同じ関係式となります。
\(V_H=Ed\) …(4)
電界\(E\)によって、クーロン力\(F_C[N]\)が働いてA面に引き寄せます。電子の電荷の大きさは電気素量\(e[C]\)なので、
\(F_C=eE\) …(5)
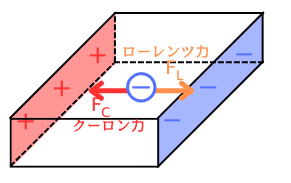
ローレンツ力\(F_L[N]\)とクーロン力\(F_C[N]\)が均衡する
B面に引き寄せるローレンツ力\(F_L\)と、A面に引き寄せるクーロン力\(F_C\)が均衡します。
(3)式=(5)式となるので、
\(evB=eE\)
⇔\(vB=E\) …(6)
(6)式を(4)式に代入すると、電位\(V\)が求まります。
\(V_H=Ed=vBd\) …(7)
(7)式に(2)式を代入して電子の速度\(v\)を消すと、
\(\displaystyle V_H=vBd=\frac{I}{entd} Bd=\frac{IB}{ent}\) …(8)
ここで、
\(\displaystyle R_H=\frac{1}{en}\) …(9)
と置いて(8)式に代入すると、
\(\displaystyle V_H=R_H\frac{IB}{t}\)
以上より、ホール効果で得られる電位\(V_H\)が求まりました。
問題文では、ホール素子の高さを\(d[m]\)としているので、
\(\displaystyle V_H=R_H\frac{IB}{d}\)となります。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和5年度上期 第三種電気主任技術者試験 理論科目A問題問11
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント