難易度
交流回路の基本的な問題です。
難解な計算はありませんが、回答には共振条件について知っている必要があります。
アプローチ方法を知らないと回答に苦労するので、類似問題を何度か解いておくと良いでしょう。
問題
図のような交流回路において、電源の周波数を変化させたところ、共振時のインダクタンスLの端子電圧\(V_L\)は\(314V\)であった。
共振周波数の値[kHz]として、最も近いものを次の（１）～（５）のうちから一つ選べ。
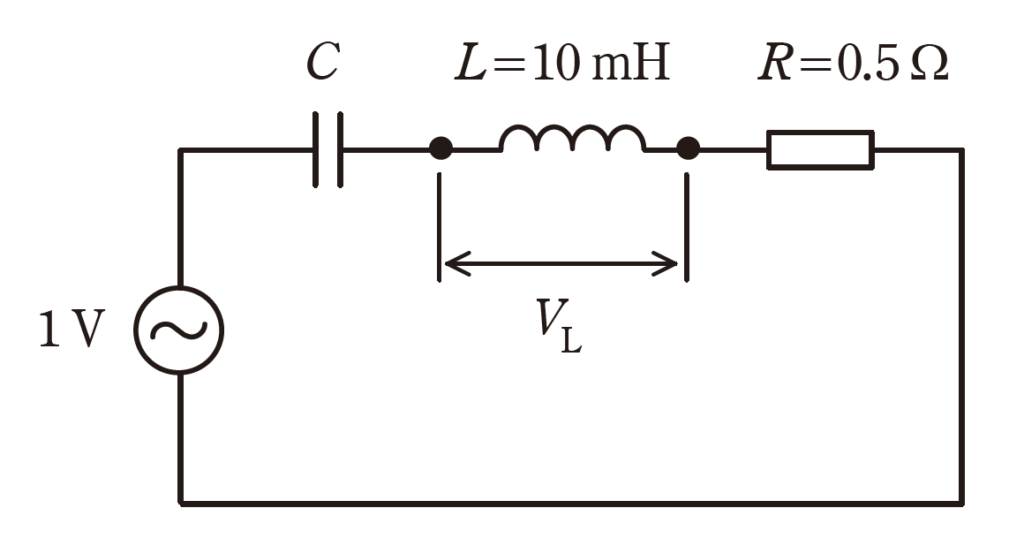
（１）2.0 （２）2.5 （３）3.0 （４）3.5 （５）4.0
答え
(２)
要点整理
インピーダンス・レジスタンス・リアクタンス
直流回路では、電流を流れにくくする要素は、レジスタンス（抵抗）のみを考えていれば十分でした。しかし、交流回路ではインピーダンス、レジスタンス、リアクタンスの３つを考える必要があります。
インピーダンスは、電気回路の計算を行う際は、\(Z\)の文字で表されます。
レジスタンス（抵抗）は\(R\)の文字、リアクタンスは\(X\)の文字で表され、
\(Z\)、\(R\)、\(X\)のどれも、単位は\([Ω]\)です。
そして、\(Z\)、\(R\)、\(X\)の関係は、
\(Z=R+jX\)
です。
式中の\(j\)は虚数単位であり、\(j^2=-1\)です。
誘導性リアクタンスとインダクタンス
リアクタンスには、誘導性リアクタンスと容量性リアクタンスがあります。
誘導性リアクタンス\(X_L[Ω]\)はインダクタ（コイル）が交流電流を流れにくくする程度を示します。
インダクタンス\(L[H]\)との関係は、
\(X_L=ωL=2πfL\)
です。上記の式の\(ω[rad/s]\)は角周波数で、\(ω=2πf\)です。
\(f[Hz]\)は周波数です。
このことから、周波数\(f\)が高くなると誘導性リアクタンス\(X_L\)も大きくなります。
容量性リアクタンスとキャパシタンス
リアクタンスには、誘導性リアクタンスと容量性リアクタンスがあります。
容量性リアクタンス\(X_C[Ω]\)はコンデンサ（キャパシタ）が交流電流を流れにくくする程度を示します。コンデンサが持つキャパシタンス\(C[F]\)との関係は、
\(\displaystyle X_C=\frac{1}{ωC}=\frac{1}{2πfC}\)
です。上記の式の\(ω\)は角周波数で、\(ω=2πf\)です。
\(f[Hz]\)は周波数です。
このことから、周波数\(f\)が高くなると容量性リアクタンス\(X_C\)は小さくなります。
共振現象
インダクタLとコンデンサCからなるLC回路や、RLC回路では、インダクタとコンデンサの間で共振する周波数があります。
共振とは、互いの電位を打ち消しあい、外からはLCのインピーダンスが0Ωに見える現象のことです。
インダクタもコンデンサも、周波数に依存してリアクタンスが変動するため、この共振現象は特定の周波数で起こります。
共振現象が起こる周波数を共振周波数と呼びます。そして、この時の角周波数は共振角周波数と呼びます。
直列接続されたRLC回路
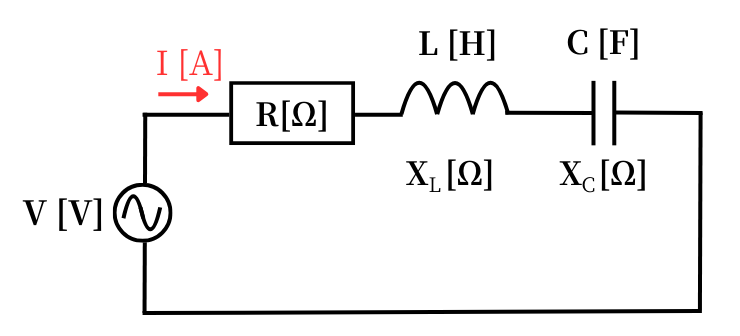
直列接続されたRLC回路のインピーダンス\(Z\)は、抵抗\(R\)、誘導性リアクタンス\(X_L\)と容量性リアクタンス\(X_C\)を使って表現すると、抵抗の直列接続のように、レジスタンスとリアクタンスをそのまま足し合わせることで表現できます。
\(\displaystyle Z=R+jX_L+\frac{X_C}{j}=R+jX_L+\frac{X_C}{j}\frac{j}{j}=R+j(X_L-X_C)\)
⇔\(\displaystyle Z=R+jωL+\frac{1}{jωC}=R+j(ωL-\frac{1}{ωC})=R+j(2πfL-\frac{1}{2πfC})\)
よって、
\(\displaystyle Z=R+j(2πfL-\frac{1}{2πfC})\)
この回路における共振周波数\(f_C\)は
\(\displaystyle 2πf_CL-\frac{1}{2πf_CC}=0\)
⇔\(\displaystyle f_C=\frac{1}{2π \sqrt{LC}}\)
共振周波数時のインピーダンスは、虚数項が0となるので、
\(Z=R\)
となります。
並列接続されたRLC回路
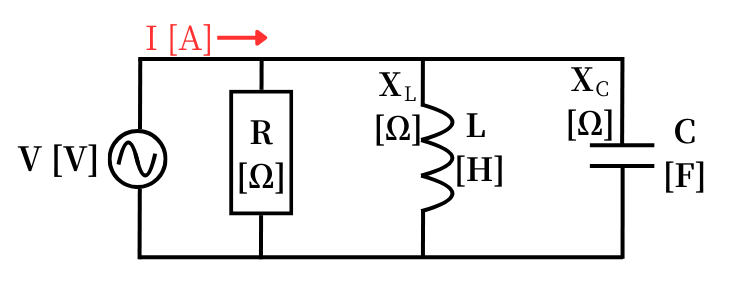
並列接続されたRLC回路のインピーダンス\(Z\)は、抵抗\(R\)、誘導性リアクタンス\(X_L\)と容量性リアクタンス\(X_C\)を使って表現すると、抵抗の並列接続のように、レジスタンスとリアクタンスの逆数を足し合わせます。
\(\displaystyle \frac{1}{Z}=\frac{1}{R}+\frac{1}{jX_L}+\frac{j}{X_C}=\frac{1}{R}+j(\frac{1}{X_C}-\frac{1}{X_L})\)
⇔\(\displaystyle \frac{1}{Z}=\frac{1}{R}+\frac{1}{jωL}+jωC=\frac{1}{R}+j(ωC-\frac{1}{ωL})=\frac{1}{R}+j(2πfC-\frac{1}{2πfL})\)
よって、RLC並列回路のインピーダンスは、
\(\displaystyle \frac{1}{Z}=\frac{1}{R}+j(2πfC-\frac{1}{2πfL})\)
となります。
この回路における共振周波数\(f_C\)は
\(\displaystyle 2πf_CL-\frac{1}{2πf_CC}=0\)
⇔\(\displaystyle f_C=\frac{1}{2π \sqrt{LC}}\)
共振周波数時のインピーダンスは、虚数項が0となるので、
\(Z=R\)
となります。
要点整理の適用
共振周波数\(f_C\)時は、コンデンサとインダクタで互いの電位を消し合いリアクタンスが\(0[Ω]\)となるので、この時のインピーダンスは、
\(Z=R=0.5[Ω]\)
となります。
この時、回路に流れる電流\(I\)は、
\(\displaystyle I=\frac{V}{Z}=\frac{1}{0.5}=2[A]\)
インダクタの電圧\(V_L\)は、
\(V_L=X_LI=2πf_CLI\)
⇔\(\displaystyle f_C=\frac{V_L}{2πLI}=\frac{314}{2π・10×10^{-3}・2}=\frac{314}{0.1256}=2500[Hz]\)
以上より、\(f_C=2.5[kHz]\)なので、（２）が回答となります。
出典元
令和５年度第三種電気主任技術者試験 理論科目Ａ問題下期問８
参考書
本ブログの管理人は、電験３種過去問マスタを使って電験３種を取りました。
とても解説が分かり易い参考書なのでお勧めです。
| 電験3種過去問マスタ 理論の20年間 |  |
| 電験3種過去問マスタ 電力の20年間 | |
| 電験3種過去問マスタ 機械の20年間 | |
| 電験3種過去問マスタ 法規の15年間 | |
コメント