【電験三種：理論】令和５年度下期　問６

難易度

直流回路の基本的な問題です。
解法はいくつかあります。
①重ねの理を使い、各電源が流す電流を合成する。
②キルヒホッフの法則から連立方程式を立てて解く。
③ミルマンの定理を使って解く。

問題

図のような直流回路において、抵抗\(6Ω\)の端子間電圧の大きさ\(V\)の値\([V]\)として、正しいものを次の（１）～（５）のうちから一つ選べ。

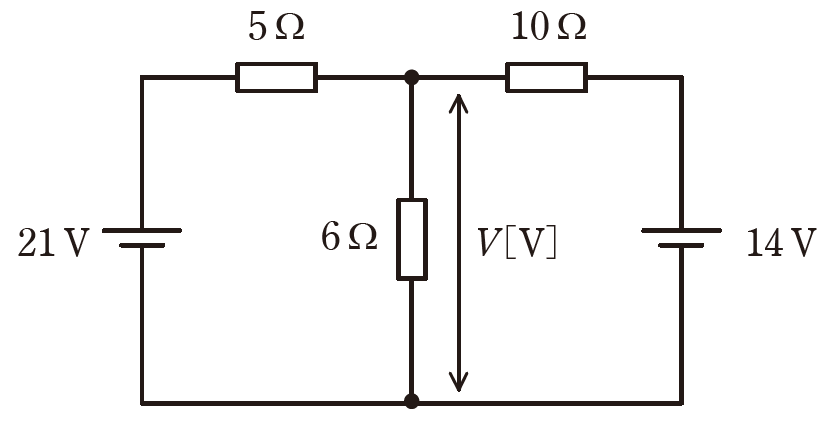
（１）２　　　（２）５　　　（３）７　　　（４）１２　　　（５）１５

---

答え

(４)

要点整理

重ねの理について

重ねの理とは、複数の電源がある回路において、回路中の電圧・電流を解析する際、それぞれの電源ごとに分離回路として解析をした後、その結果を、足し合わせる（重ねる）ことで、求めたい電圧、電流が求まるという手法です。
これがどういうことかを、図を使用しながら解説します。

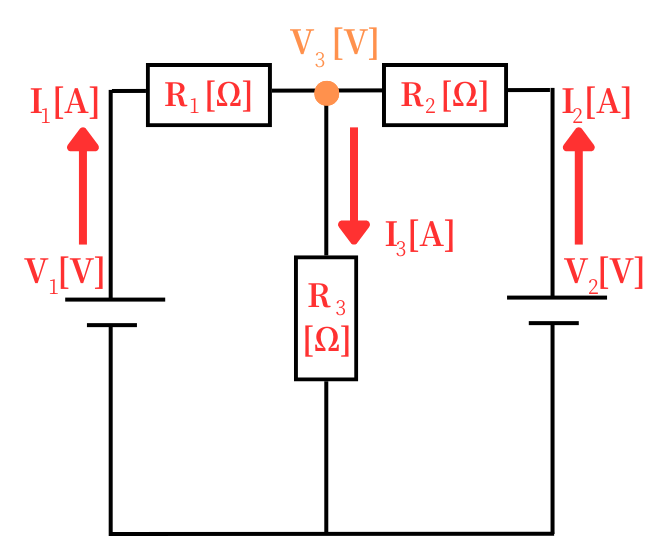
上図のように\(V_1\)、\(V_2\)の２つの電源がある回路を解析します。

【手順①】下図のように、\(V_1\)だけの回路、\(V_2\)だけの回路の２つの分離回路として解析をしていきます。

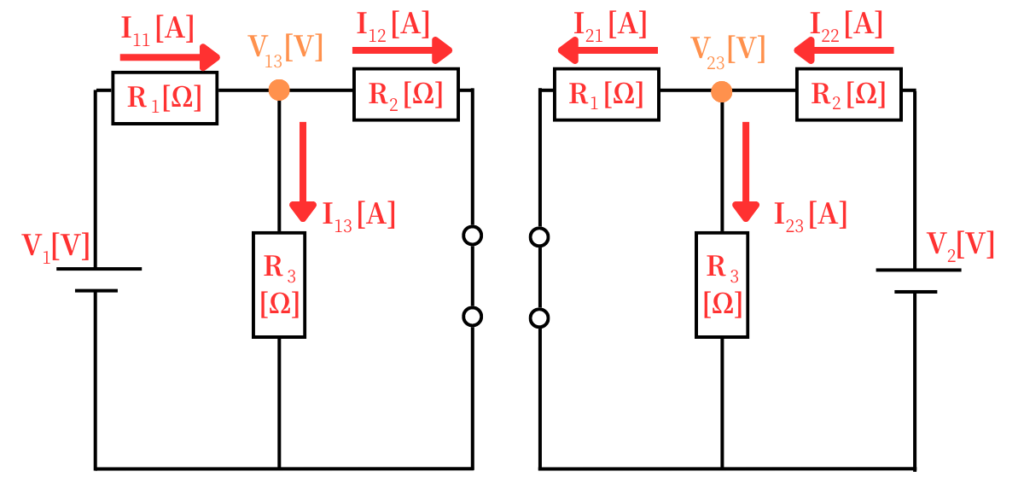
【手順②】解析した結果を足し合わせます。
\(I_1=I_{11}+(-I_{21})\)
\(I_2=-I_{12}+I_{22}\)
\(I_3=I_{13}+I_{23}\)
\(V_3=V_{13}+V_{23}\)

以上で、求めたい電圧、電流が求まりました。

キルヒホッフの法則による回路解析

キルヒホッフの電圧則は、回路網中の任意の閉路において、一巡する経路に含まれる起電力（電源）の総和と電圧降下の総和は等しいという法則です。
この法則を使って、二つの電源を持つ回路の解析ができます。

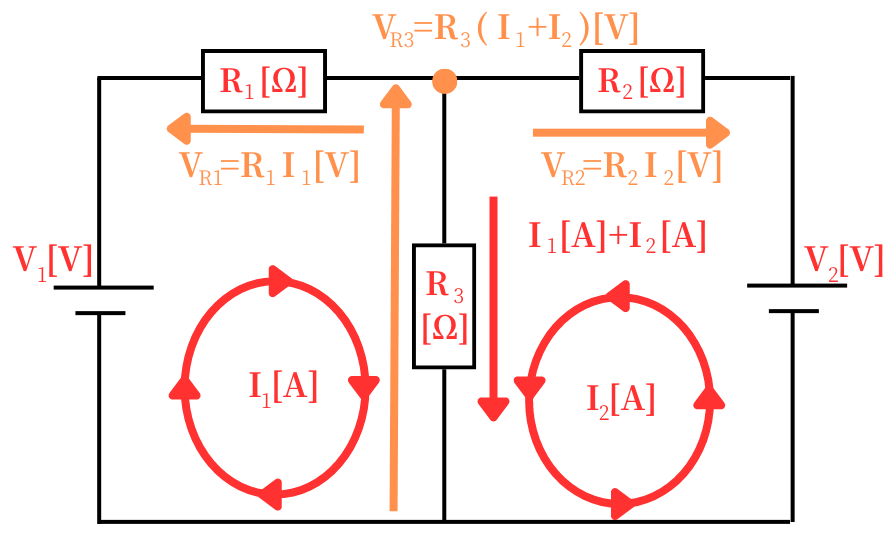
まず、二つの電源回路から、上図のようなループ電流\(I_1\)、\(I_2\)が流れているとします。
一巡する経路に含まれる電源起電力を左辺、電圧降下を右辺に記述しますと、
\(\begin{eqnarray}
\left\{
\begin{array}{l}
V_1=V_{R1}+V_{R3}\\
V_2=V_{R2}+V_{R3}
\end{array}
\right.
\end{eqnarray}\)

↓　各抵抗、電流を代入すると、

\(\begin{eqnarray}
\left\{
\begin{array}{l}
V_1=R_1I_1+R_3(I_1+I_2)\\
V_2=R_2I_2+R_3(I_1+I_2)
\end{array}
\right.
\end{eqnarray}\)

の連立方程式が立てられます。この連立方程式を解くことで欲しい点の電圧・電流値が求まります。

ミルマンの定理について

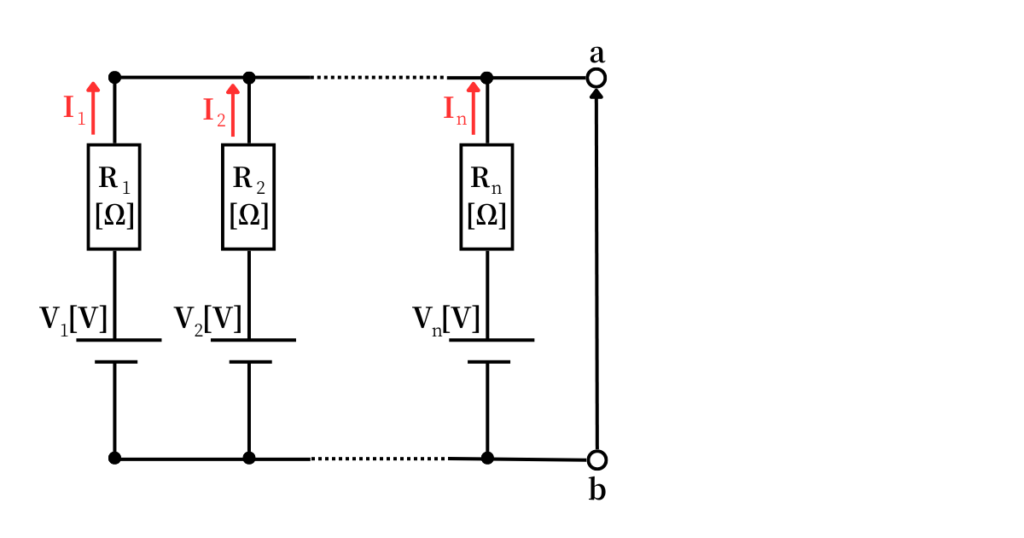
上図のように、各枝路に電源と抵抗が並列に接続されている回路を考えます。
各抵抗を流れる電流値を\(I_1,I_2,…,I_n\)とすると、

\(I_1+I_2+…+I_n=0\)　　　………①

となります。
次に、各電源の各導線における電位差を考えると、

\(V_1-R_1I_1=V_{ab}\)　⇔　\(\displaystyle I_1=\frac{V_1-V_{ab}}{R_1}\)
\(V_2-R_2I_2=V_{ab}\)　⇔　\(\displaystyle I_2=\frac{V_2-V_{ab}}{R_2}\)

　　　︙

\(V_n-R_nI_n=V_{ab}\)　⇔　\(\displaystyle I_n=\frac{V_n-V_{ab}}{R_n}\)　　　………②

なるので、②を①に代入すると、

\(\displaystyle \frac{V_1-V_{ab}}{R_1}+\frac{V_2-V_{ab}}{R_2}+…+\frac{V_n-V_{ab}}{R_n}=0\)

⇔\(\displaystyle (\frac{1}{R_1}+\frac{1}{R_2}+…\frac{1}{R_n})V_{ab}=(\frac{V_1}{R_1}+\frac{V_2}{R_2}+…\frac{V_n}{R_n})\)

⇔\(\displaystyle V_{ab}=\frac{\frac{V_1}{R_1}+\frac{V_2}{R_2}+…\frac{V_n}{R_n}}{(\frac{1}{R_1}+\frac{1}{R_2}+…\frac{1}{R_n})}\)

⇔\(\displaystyle V_{ab}=\frac{\sum_{i=1}^{n}\frac{V_i}{R_i}}{\sum_{i=1}^{n}\frac{1}{R_i}}\)

と導くことができます。

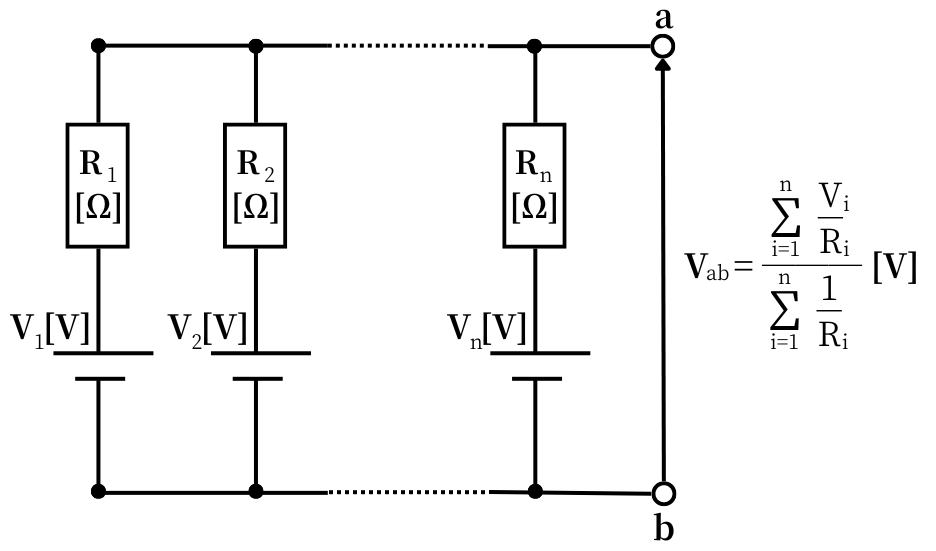
内部抵抗を持つ電池を並列接続したとき、このような回路となります。

　

要点整理の適用

重ねの理による解

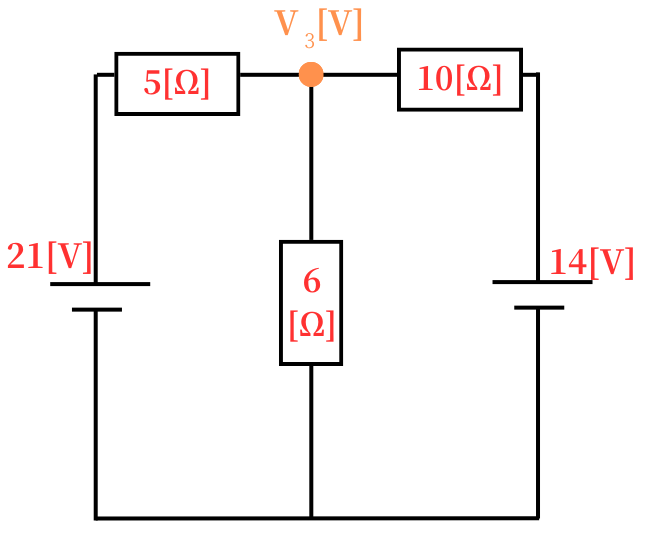
図の回路を重ねの理で、それぞれの電源ごとに回路解析をします。

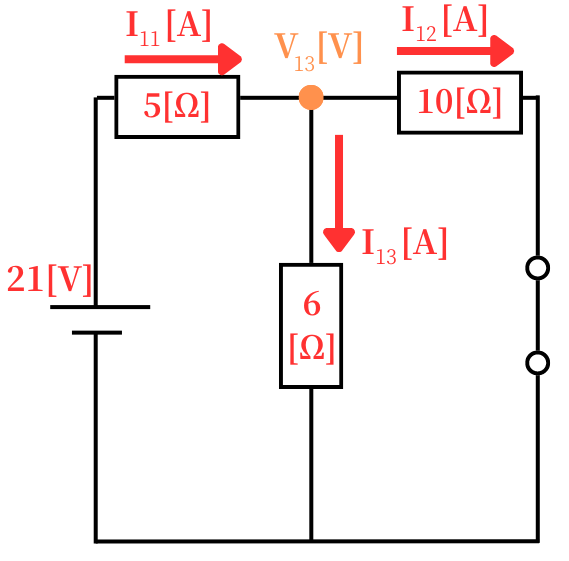	左図の回路を解析すると、 \(I_{11}=2.4[A]\) \(I_{12}=0.9[A]\) \(I_{13}=1.5[A]\) \(V_{13}=9[V]\)
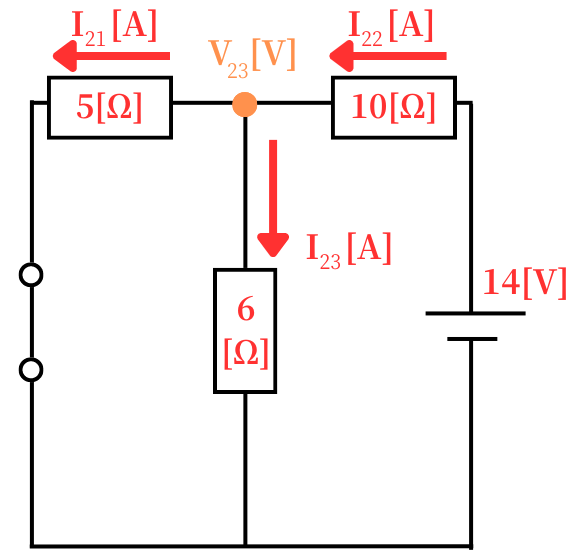	左図の回路を解析すると、 \(I_{21}=0.6[A]\) \(I_{22}=1.1[A]\) \(I_{23}=0.5[A]\) \(V_{23}=3[V]\)

以上から、\(V_3=V_{13}+V_{23}=9+3=12[V]\)
\(V_3=12[V]\)なので（４）が回答となります。

キルヒホッフの法則による解

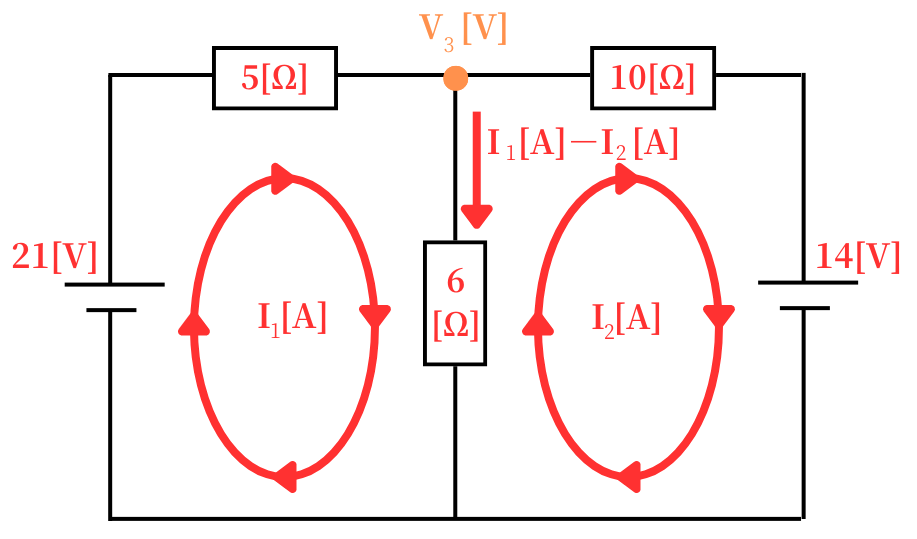
キルヒホッフの法則から、連立方程式を立式すると、

\(\begin{eqnarray}
\left\{
\begin{array}{l}
21=5I_1+6(I_1-I_2)\\
14=-10I_2+6(I_1-I_2)
\end{array}
\right.
\end{eqnarray}\)
⇓
\(\begin{eqnarray}
\left\{
\begin{array}{l}
21=11I_1-6I_2　　　………①\\
14=6I_1-16I_2　　　………②
\end{array}
\right.
\end{eqnarray}\)
⇓
①を変形すると、
\(\displaystyle I_2=\frac{11I_1-21}{6}\)　　　………③

③を②に代入すると、
\(\displaystyle 14=6I_1-\frac{16}{6}(11I_1-21)\)
⇔\(84=36I_1-176I_1+336\)
⇔\(140I_1=252\)
⇔\(I_1=1.8[A]\)　　　………④

④を③に代入すると、
\(\displaystyle I_2=\frac{11・1.8-21}{6}=-0.2[A]\)　　　………⑤

次に、\(V_3\)を求める。
\(V_3=6(I_1-I_2)\)　　　………⑥
なので、⑥に④・⑤を代入すると、
\(V_3=6(1.8-(-0.2))=12[V]\)

以上より、\(V_3=12[V]\)なので（４）が回答となります。

ミルマンの定理による解

問題の図を、ミルマンの定理を適用しやすいように書き直します。
\(6[Ω]\)の抵抗には、\(0[V]\)の電源がつながっていることとします。

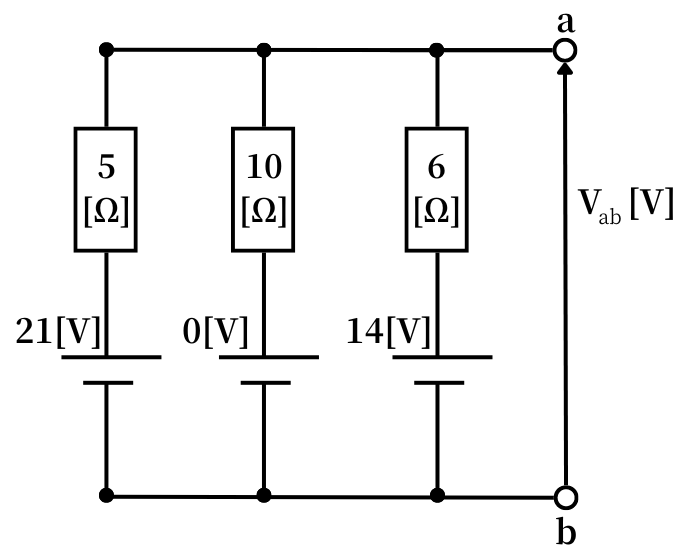
\(\displaystyle V_{ab}=\frac{\sum_{i=1}^{3}\frac{V_i}{R_i}}{\sum_{i=1}^{3}\frac{1}{R_i}}\)

⇔\(\displaystyle V_{ab}=\frac{\frac{21}{5}+\frac{14}{10}+\frac{0}{6}}{\frac{1}{5}+\frac{1}{10}+\frac{1}{6}}\)

⇔\(\displaystyle V_{ab}=\frac{\frac{28}{5}}{\frac{7}{15}}\)

⇔\(\displaystyle V_{ab}=12[V]\)

以上より、\(V_{ab}=12[V]\)なので（４）が回答となります。

出典元

令和５年度第三種電気主任技術者試験　理論科目Ａ問題下期問６

参考書