難易度
コンデンサのΔ-Y変換に関する問題です。
(a)は、Δ-Y変換に関して学ぶ必要がありますが、Δ-Y変換に関して考え方を理解しておけば、問題なく回答出来る事と思います。
(b)は、直並列のコンデンサの合成容量を求めるだけです。
(b)は簡単ですが、(a)が解けていないと一緒に落としてしまうので、Δ-Y変換について理解しておきたいです。
問題
図1の端子a-d間の合成静電容量について、次の(a)及び(b)の問に答えよ。
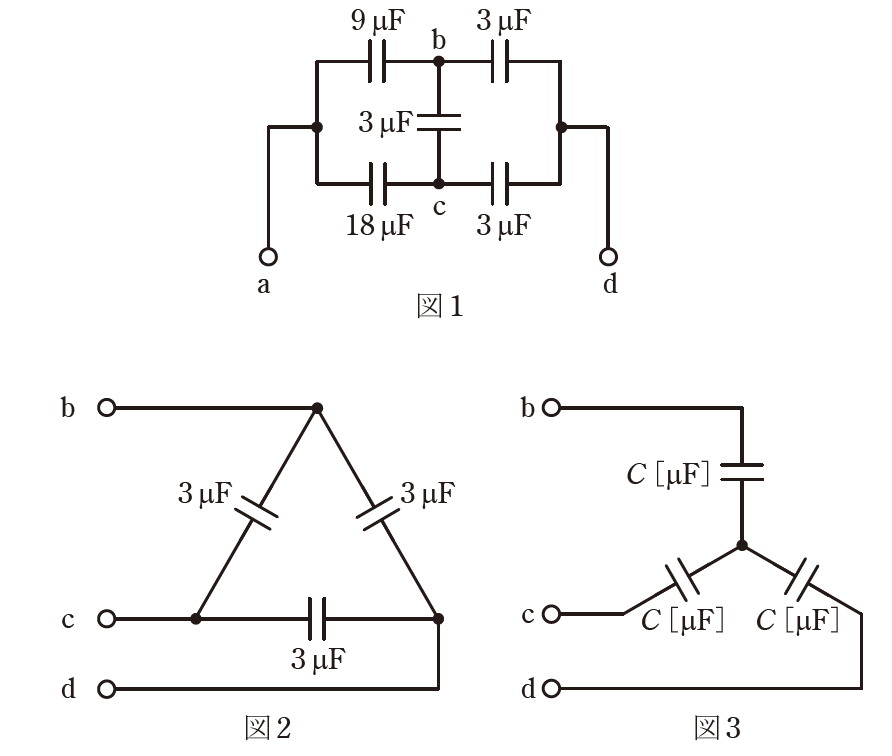
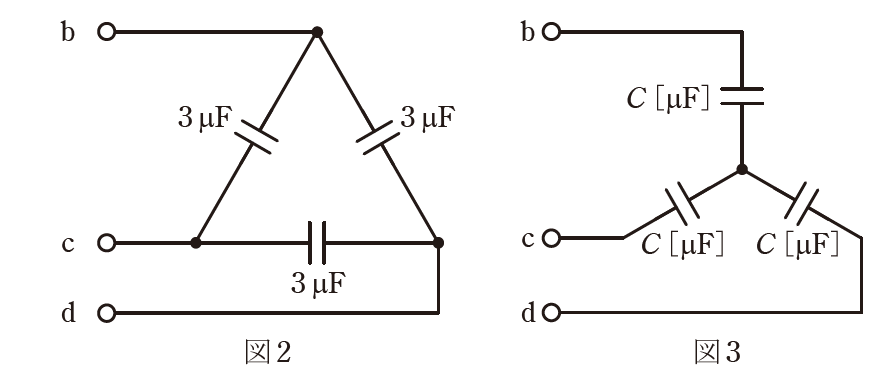
(a) 端子b-c-d間は図2のようにΔ結線で接続されている。これを図3のようにY結線に変換したとき、電気的に等価となるコンデンサCの値[μF]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)1.0 (2)2.0 (3)4.5 (4)6.0 (5)9.0
(b) 図3を用いて、図1の端子b-c-d間をY結線回路に変換したとき、図1の端子a-d間の合成静電容量\(C_o\)の値[μF]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)3.0 (2) 4.5 (3) 4.8 (4) 6.0 (5) 9.0
答え
(a) (5)
(b) (3)
要点整理
Δ-Y変換
解析する回路によってはΔ型に結線された回路や、Y型に結線された回路が有ります。それらをΔ結線、Y結線と呼び、三相交流回路では頻出します。
Δ結線では扱い難い場合、Y結線では扱い難い場合があります。
その時に、Y-Δ変換をしてΔ結線をY結線に変換する、逆にY結線をΔ結線に変換することで、問題を解決しやすくなります。
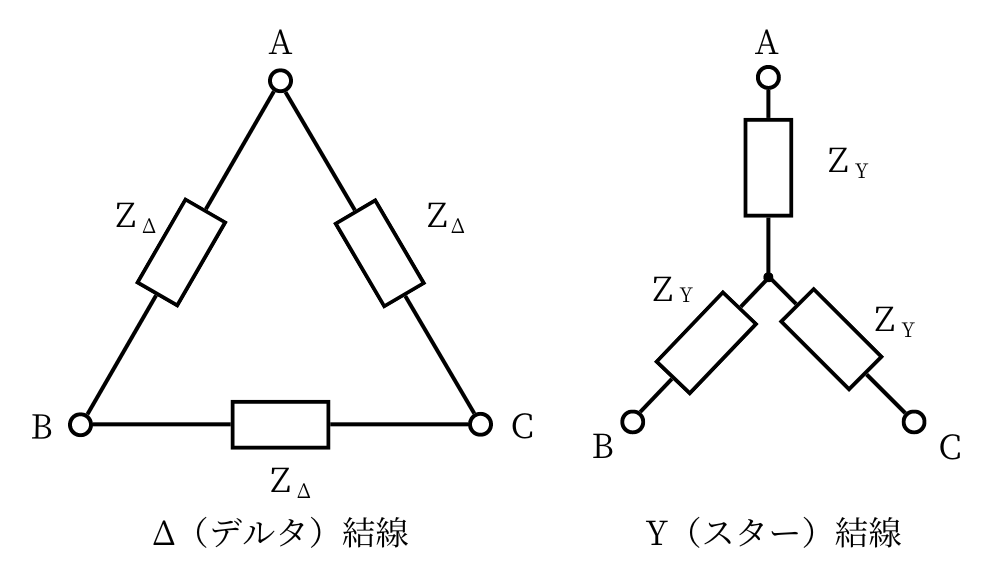
Δ結線のインピーダンスを\(Z_\Delta\)
Y結線のインピーダンスを\(Z_Y\)
とし、AB間、BC間、CA間の抵抗が全て同じ抵抗値の物が接続されているとします。
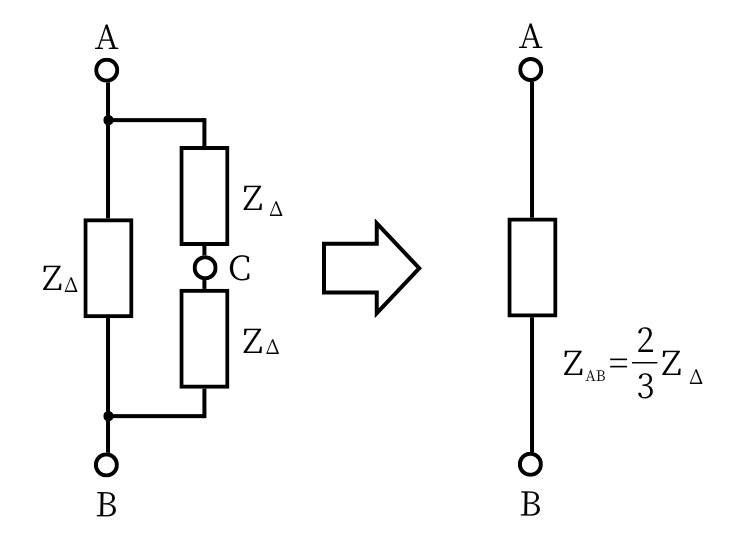
まずは、Δ結線のAB間のインピーダンスについて検討します。
Δ結線のAB間のインピーダンスを\(Z_{AB}\)としたとき、
\(\displaystyle \frac{1}{Z_{AB}}=\frac{1}{Z_\Delta}+\frac{1}{2Z_\Delta}=\frac{3}{2Z_\Delta}\)
⇔\(\displaystyle Z_{AB}=\frac{2}{3}Z_\Delta\) ……①
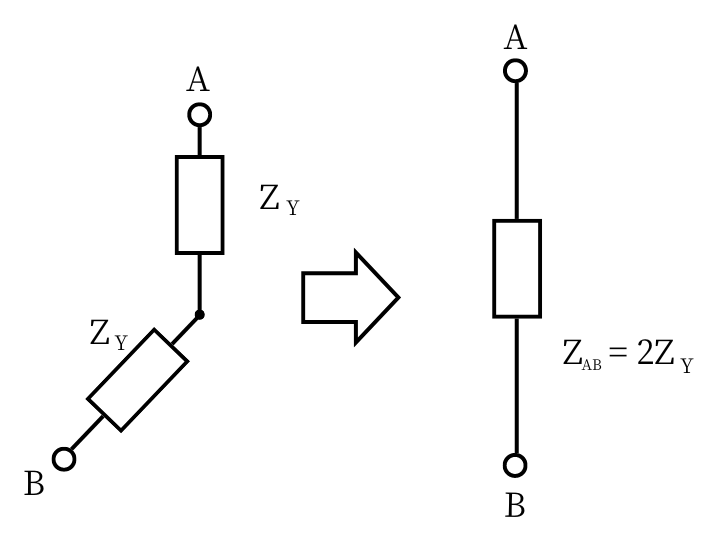
次に、Y結線のAB間のインピーダンスについて検討します。
Y結線のAB間のインピーダンスも同じく\(Z_{AB}\)とすると、
\(Z_{AB}=2Z_Y\) ……②
となります。
最後に、①=②より、
\(\displaystyle \frac{2}{3}Z_\Delta=2Z_Y\)
したがって、
\(Z_\Delta=3Z_Y\)
⇔\(\displaystyle Z_Y=\frac{1}{3}Z_\Delta\)
の関係が導き出せます。
注意点としては、全てのインピーダンスが同じ抵抗という前提の元、簡略化しています。
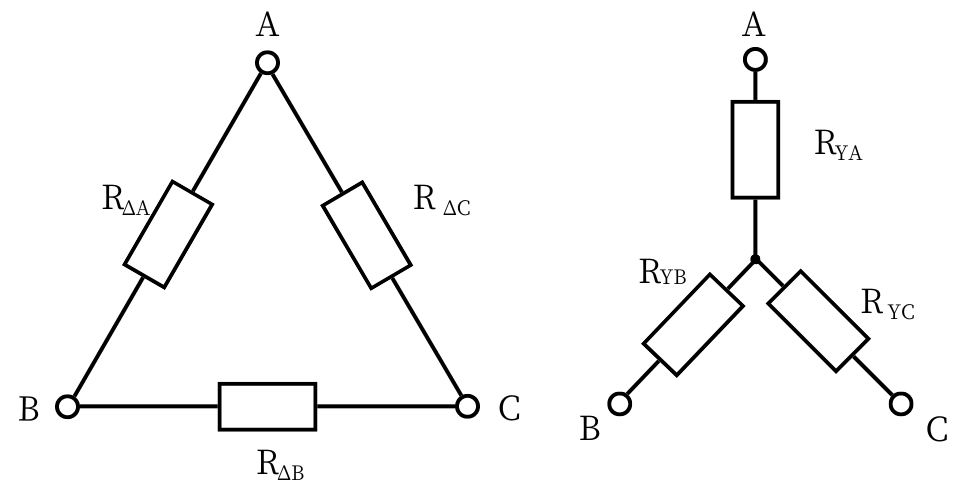
全部の抵抗値が違う場合のY-Δ変換の公式は、
\(\displaystyle Z_{YA}=\frac{Z_{\Delta B}Z_{\Delta C}}{Z_{\Delta A}+Z_{\Delta B}+Z_{\Delta C}}\)
\(\displaystyle Z_{YB}=\frac{Z_{\Delta C}Z_{\Delta A}}{Z_{\Delta A}+Z_{\Delta B}+Z_{\Delta C}}\)
\(\displaystyle Z_{YC}=\frac{Z_{\Delta A}Z_{\Delta B}}{Z_{\Delta A}+Z_{\Delta B}+Z_{\Delta C}}\)
です。導出するのは手間なので、ここでは割愛します。
\(Z_{\Delta A}=Z_{\Delta B}=Z_{\Delta C}=Z_{\Delta }\)とした場合、
\(\displaystyle Z_Y=\frac{1}{3}Z_\Delta\)
コンデンサの並列接続時の合成容量
高校物理レベルの余談となりますが、静電容量が\(C_1\)のコンデンサと\(C_2\)のコンデンサが並列接続した時の合成容量\(C\)を考えます。結論から述べると、
並列接続時の合成容量\(C\)は、
\(C=C_1+C_2\)
です。この式について証明します。
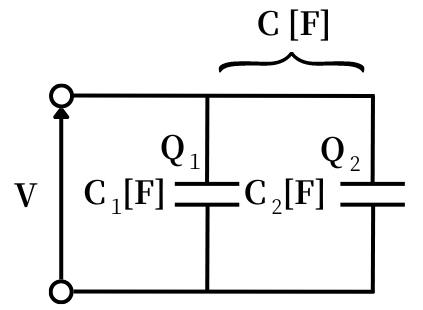
二つのコンデンサの電荷・静電容量・電圧の関係式は、
\(Q_1=C_1V\) ………①
\(Q_2=C_2V\) ………②
二つのコンデンサに蓄えられる電荷量
\(Q=Q_1+Q_2\) ………③
合成の電荷・静電容量・電圧の関係式は
\(Q=CV\) ………④
④式のQに①・②・③式を代入すると
\(Q=Q_1+Q_2=C_1V+C_2V=(C_1+C_2)V=CV\)
⇔\(C=C_1+C_2\)
よって、並列接続時の静電容量の式について証明出来ました。
コンデンサの並列接続時の合成容量
静電容量が\(C_1\)のコンデンサと\(C_2\)のコンデンサが直列接続した時の静電容量\(C\)を考えます。結論から述べると、
直列接続時の合成容量\(C\)は、
\(\displaystyle \frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}\)
です。この式について証明します。
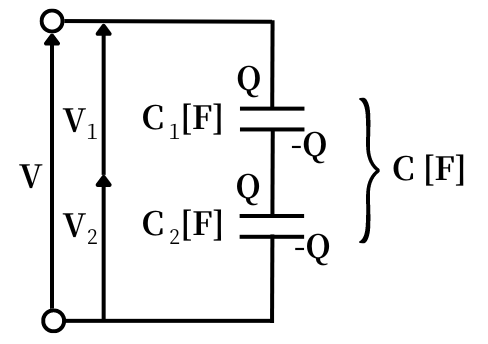
直列接続時は、二つのコンデンサに蓄えられる電荷は両方とも\(Q[C]\)です。
そのため、二つのコンデンサの電荷・静電容量・電圧の関係式は
\(Q=C_1V_1\)
⇔\(\displaystyle V_1=\frac{Q}{C_1}\) ………①
\(Q=C_2V_2\)
⇔\(\displaystyle V_2=\frac{Q}{C_2}\) ………②
各コンデンサの電圧は、
\(V=V_1+V_2\) ………③
合成の電荷・静電容量・電圧の関係式は
\(Q=CV\)
⇔\(\displaystyle C=\frac{Q}{V}\) ………④
④式のVに①・②・③式を代入すると
\(\displaystyle C=\frac{Q}{V}=\frac{Q}{V_1+V_2}=\frac{Q}{\frac{Q}{C_1}+\frac{Q}{C_2}}=\frac{1}{\frac{1}{C_1}+\frac{1}{C_2}}\)
⇔\(\displaystyle \frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}\)
回答解説
問(a)

Δ-Y変換から、Δ結線のインピーダンス\(Z_Δ\)は、Y結線のインピーダンス\(Z_Y\)に
\(Z_Δ=3Z_Y\)
⇔\(Z_Y=\frac{1}{3}Z_Δ\)
と、変換できます。
リアクタンス\(X\)においても、インピーダンスと同様に
\(X_Δ=3X_Y\) ………①
です。
リアクタンスと静電容量の関係式は、\(\displaystyle X_C=\frac{1}{jωC}\)なので、
Δ結線のリアクタンスと静電容量は
\(\displaystyle X_Δ=\frac{1}{jωC_Δ}\) ………②
Y結線のリアクタンスと静電容量は
\(\displaystyle X_Y=\frac{1}{jωC_Y}\) ………③
とします。
①式に②・③式を代入します。このとき、\(C_Δ=3[μF]\)なので、
\(\displaystyle \frac{1}{jωC_Δ}=3×\frac{1}{jωC_Y}\)
⇔\(C_Y=3C_Δ=3×3=9[μF]\)
以上より、Y結線に変換したとき、電気的に等価となるコンデンサCの値[F]は、
(5)\(C_Y=9[μF]\)です。
問(b)
問(a)から、Δ-Y変換すると、\(C_Y=9[μF]\)となることがわかりました。
その結果を踏まえ、問題の回路図に適用すると、下図のように変換できます。
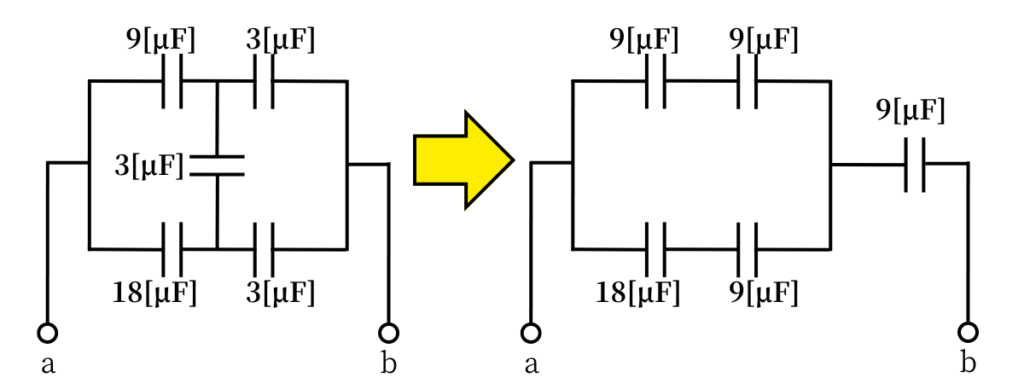
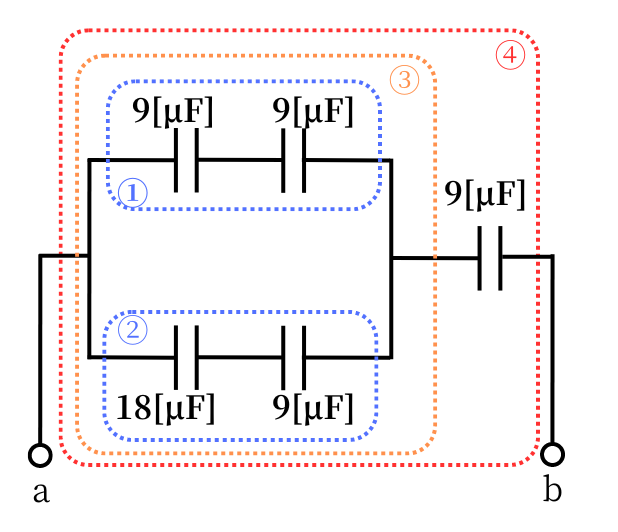
コンデンサの直並列の合成容量の計算から
①の範囲の静電容量\(C_1\)は、
\(\displaystyle C_1=\frac{9×10^{-6}・9×10^{-6}}{9×10^{-6}+9×10^{-6}}=4.5[μF]\)
②の範囲の静電容量\(C_2\)は、
\(\displaystyle C_2=\frac{18×10^{-6}・9×10^{-6}}{18×10^{-6}+9×10^{-6}}=6[μF]\)
③の範囲の静電容量\(C_3\)は、
\(C_3=C_2+C_1=4.5+6=10.5[μF]\)
④の範囲の静電容量\(C_4\)は、
\(\displaystyle C_4=\frac{10.5×10^{-6}・9×10^{-6}}{10.5×10^{-6}+9×10^{-6}}≒4.8[μF]\)
したがって、(3)4.8 が答えです。
出典元
令和5年度第三種電気主任技術者試験 理論科目B問題下期問17
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント