難易度
クーロン力による電子の加速に関する問題です。
高校生で学ぶ等速直線運動を理解していれば十分に解ける簡単な問題です。
問題
次の文章は、真空中における電子の運動に関する記述である。
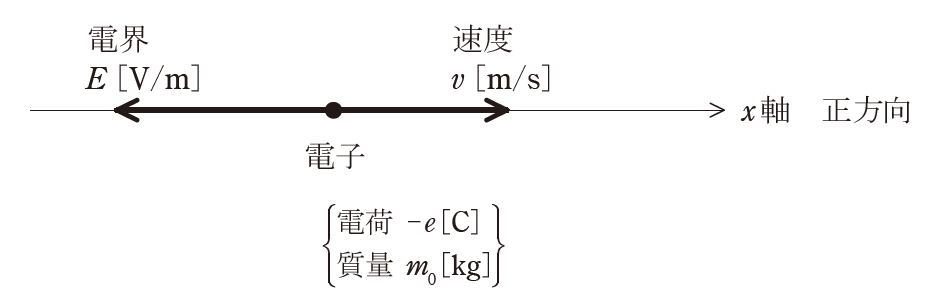
図のように、x軸上の負の向きに大きさが一定の電界\(E[V/m]\)が存在しているとき、x軸上に電荷が\(-e[C]\)(\(e\)は電荷の絶対値)、質量\(m_0[kg]\)の1個の電子を置いた場合を考える。
x軸の正方向の電子の加速度を\(a[m/s^2]\)とし、また、この電子に加わる力の正方向をx軸の正方向にとったとき、電子の運動方程式は
\(m_0a=\)ア ………①
となる。①式から電子は等加速度運動をすることがわかる。したがって、電子の初速度を零としたとき、x軸の正方向に向かう電子の速度\(v[m/s]\)は時間\(t[s]\)のイ関数となる。
また、電子の走行距離\(x_{dis}[m]\)は時間\(t[s]\)のウ関数で表される。
さらに、電子の運動エネルギーは時間\(t[s]\)のエで増加することがわかる。
ただし、電子の速度\(v[m/s]\)はその質量の変化が無視できる範囲とする。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | \(eE\) | 一次 | 二次 | 1乗 |
| (2) | \(\displaystyle \frac{1}{2}eE\) | 二次 | 一次 | 1乗 |
| (3) | \(eE^2\) | 一次 | 二次 | 2乗 |
| (4) | \(\displaystyle \frac{1}{2}eE\) | 二次 | 一次 | 2乗 |
| (5) | \(eE\) | 一次 | 二次 | 2乗 |
答え
(5)
要点整理
クーロン力とは
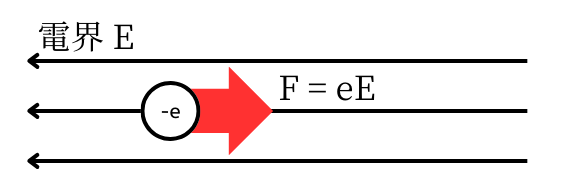
電界\(E\)の中にある電荷\(-e\)の電子には
\(F=eE\)
のクーロン力が働きます。
電子は負電荷であるため、電界の向きとは逆方向に力が働きます。
運動方程式

質量\(m\)の物体に、力\(F\)が働くとき、この物体には
\(F=mα\) ………①
で決まる加速度\(α\)が生じます。
加速度\(α\)・速度\(v\)・位置\(x\)の関係は、
\(\displaystyle v=\frac{dx}{dt}\) ………②
⇔\(\displaystyle x=\int v dt\) ………③
\(\displaystyle α=\frac{dv}{dt}=\frac{d^2x}{dt^2}\) ………④
⇔\(\displaystyle v=\int α dt=αt \) ………⑤
③・⑤式から、
\(\displaystyle x=\int v dt=\int αt dt=\frac{1}{2}αt^2\) ………⑥
運動エネルギー
力\(F\)で、質量\(m\)の物質を距離\(x\)だけ動かした時、
\(W=\int F dx\) ………①
です。
運動方程式の式 \(\displaystyle F=mα\) ………②
加速度\(α\)と速度\(v\)の関係式 \(\displaystyle α=\frac{dv}{dt}\) ………③
速度\(v\)と位置\(x\)の関係式 \(\displaystyle v=\frac{dx}{dt}\) ………④
を使用すると、下記の通り式を展開できます。
\(\displaystyle \begin{eqnarray}
W &=& \int F dx ②を代入 \\
&=& \int mα dx ③を代入 \\
&=& \int m\frac{dv}{dt}dx dvとdxを入れ替える \\
&=& \int m \frac{dx}{dt}dv ④を代入 \\
&=& \int mv dv 積分の計算をする\\
&=&\frac{1}{2}mv^2
\end{eqnarray}\)
要点整理の適用
ア
電子に加わる力は、クーロン力の式から、\(F=eE\)です。
運動方程式の式は、\(F=m_0α\) なので、
\(m_0α=eE\) ………①
が答えです。
イ
電子の速度\(v[m/s]\)は、加速度\(α\)と、時間\(t[s]\)を使って、
\(v= \int αdt = αt\) ………②
です。①式を変形すると
\(\displaystyle α=\frac{eE}{m_0}\) ………③
なので、③式を②式に代入すると、
\(\displaystyle v=\frac{eE}{m_0}t\) ………④
となります。したがって、一次関数が答えです。
ウ
電子の走行距離\(x_{dis}\)は、
\(\displaystyle x_{dis}=\int vdt = \int αt dt = \frac{1}{2}αt^2 \) ………⑤
です。③式を⑤式に代入すると、
\(\displaystyle x_{dis}=\frac{1}{2}\frac{eE}{m_0}t^2\)
となります。したがって、二次関数が答えです。
エ
電子の運動エネルギー\(W\)は、
\(\displaystyle W=\frac{1}{2}m_0v^2\) ………⑥
です。④式を⑥式に代入すると、
\(\displaystyle W=\frac{1}{2}m_0 \left( \frac{eE}{m_0}t \right)^2 \)
⇔\(\displaystyle W=\frac{e^2E^2}{2m_0}t^2 \)
となります。したがって、2乗が答えです。
以上より、(5)が答えです。
出典元
令和5年度第三種電気主任技術者試験 理論科目A問題下期問12
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント