難易度
コンデンサから放電するときの過渡現象の論説問題です。
過渡現象の単元は解き方に慣れるまでは難易度が高いです。
この問題は、この単元の中は中程度の難易度です。
引っかけ問題というほどではありませんが、回答の選択肢の言葉の意味をしっかりと考えないとミスリードされてしまうかもしれません。
問題
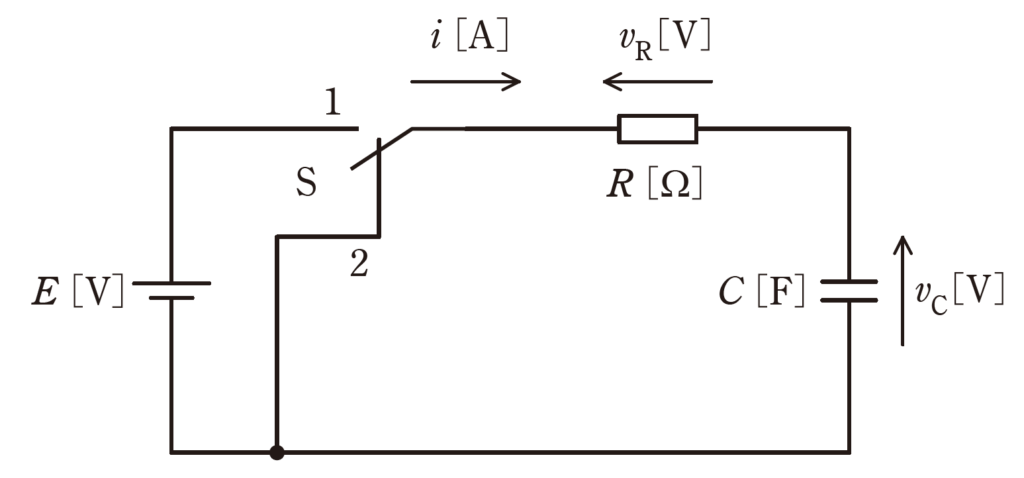
図のように、電圧\(E[V]\)の直流電源、スイッチS、\(R[Ω]\)の抵抗及び静電容量\(C[F]\)のコンデンサからなる回路がある。
この回路において、スイッチSを１側に接続してコンデンサを十分に充電した後、時刻\(t=0s\)でスイッチSを１側から２側に切り替えた。
２側に切り替えた以降の記述として、誤っているものを次の（１）～（５）のうちから一つ選べ。
ただし、自然対数の底は、2.718とする。
（１）回路の時定数は、\(C\)の値\([F]\)に比例する。
（２）コンデンサの端子電圧\(v_C[V]\)は、\(R\)の値\([Ω]\)が大きいほど緩やかに減少する。
（３）時刻\(t=0s\)から回路の時定数だけ時間が経過すると、コンデンサの端子電圧\(v_C[V]\)は直流電源の電圧\(E[V]\)の\(0.368\)倍に減少する。
（４）抵抗の端子電圧\(v_R[V]\)の値は負である。
（５）時刻\(t=0s\)における回路の電流\(i[A]\)は、\(C\)の値\([F]\)に関係する。
答え
(５)
要点整理
初等解析法を使った過渡解析
過渡現象を初等解析法で解く方法の流れは以下の流れです。
①回路図から微分方程式を作る
②過渡状態の\(v_C\)の電圧：\(v_{Ct}\)を解析する
③定常状態の\(v_C\)の電圧：\(v_{Cs}\)を解析する
④\(v_C=v_{Ct}+v_{Cs}\)とすることで、コンデンサCの電圧の式を組み立てる
⑤初期条件\(t=0[s]\)から、\(v_C\)の式中の未定だった係数を導き出す
⇒完了
文字に手順を起こすと少々手順が多いように見えますが、実際多いです。
しかし、ラプラス変換で解く方法や、微分方程式から数学的に解く方法よりは圧倒的に楽で早いです。
コンデンサの電荷\(Q\)と静電容量\(C\)と電圧\(V\)の関係式から、
\(Q=CV\) ………(1)
回路中に流れる電流を\(i\)としたとき、電流は、電荷の流れなので、
\(\displaystyle i=\frac{dq}{dt}=\frac{dv_C}{dt}\) ………(2)
(2)式を使って、２側に切り替えた後の回路の微分方程式を立てると、
\(v_R+v_C=0\)
⇔\(iR+v_C=0\)
⇔\(\displaystyle RC\frac{dv_C}{dt}+v_C=0\) ………(3)
となります。
この(3)式を使って、過渡状態、定常状態の２つの状態について解析していきます。
過渡状態
過渡状態の時の\(v_C\)は、\(v_{Ct}\)とします。
このとき、(3)式中の変数に下記(4)・(5)式をあてはめます。
\(v_{Ct}=ke^{st}\) ………(4)
(4)式をtで微分すると
\(\displaystyle \frac{dv_{Ct}}{dt}=ske^{st}\) ………(5)
(3)式は、
\(\displaystyle RCske^{st}+ke^{st}=(1+RCs)ke^{st}=0\) ………(6)
となります。(6)式を満たすsは、
\(\displaystyle s=-\frac{1}{RC}\) ………(7)
(7)式を(4)式に代入すると、
\(\displaystyle v_{Ct}=ke^{-\frac{1}{RC}t}\) ………(8)
そして、過渡現象における時定数\(τ\)は、先ほど求めた\(s\)の逆数なので、
\(\displaystyle τ=\frac{1}{s}=RC\) ………(9)
定常状態
定常状態になると、電流・電圧の変化は無くなるので、(3)式中の微分項は0となります。
定常状態の\(v_C\)を、\(v_{Cs}\)としますと、
\(\displaystyle \frac{dv_{Cs}}{dt}=0\) …(10)
(10)を(3)式に代入すると、
\(\displaystyle v_{Cs}=0\) …(11)
まとめ
過渡状態\(v_{Ct}\)、定常状態\(v_{Cs}\)を足し合わせることで、\(v_C\)の式を導き出せます。
(8)式と、(11)式から、
\(v_C=v_{Ct}+v_{Cs}=ke^{-\frac{1}{RC}t}+0\) …(12)
係数kを初期条件から求めます。
２側に切り替えた直後\(t=0\)のコンデンサの電圧は、\(v_C(0)=E[V]\)なので、
\(t=0\) ………(13)
\(v_C(0)=E\) ………(14)
この２つの初期条件が得られます。
\(\begin{eqnarray}
v_C(0)&=&v_{Ct}+v_{Cs} \\
&=&ke^{st}+0 \\
&=&ke^0 \\
&=&k ………(15)
\end{eqnarray}\)
(14)式、(15)式から
\(k=E\) ………(16)
が求まります。
(16)式を(12)式に代入すると、
\(\displaystyle v_C=Ee^{-\frac{1}{RC}t}\) ………(17)
時定数経過した時、すなわち\(t=τ=RC\)のとき、
\(\displaystyle v_C=Ee^{-1}=\frac{E}{e}=\frac{E}{2.718}=0.368E\) ………(18)
要点整理の適用
（１）回路の時定数は、\(C\)の値\([F]\)に比例する。
要点整理(９)式
\(\displaystyle τ=\frac{1}{s}=RC\) ………(9)
時定数\(τ\)は、\(C\)の値に比例しますので正しいです。
（２）コンデンサの端子電圧\(v_C[V]\)は、\(R\)の値\([Ω]\)が大きいほど緩やかに減少する。
時定数\(τ[s]\)の数字が大きいほど、変化は緩やかになります。
要点整理(９)式
\(\displaystyle τ=\frac{1}{s}=RC\) ………(9)
したがって、時定数\(τ\)は、\(R\)の値に比例して大きくなります。
そして、\(τ\)大きくなると緩やかになりますので、正しいです。
（３）時刻\(t=0s\)から回路の時定数だけ時間が経過すると、コンデンサの端子電圧\(v_C[V]\)は直流電源の電圧\(E[V]\)の\(0.368\)倍に減少する。
時定数経過した時、すなわち\(t=τ\)のとき、要点整理の(18)式
\(\displaystyle v_C=Ee^{-1}=\frac{E}{e}=\frac{E}{2.718}=0.368E\) ………(18)
したがって、正しいです。
（４）抵抗の端子電圧\(v_R[V]\)の値は負である。
回路方程式は
\(v_R+v_C=0\)
であるため、
\(v_R=-v_C\)となります。
したがって、負となりますので正しいです。
（５）時刻\(t=0s\)における回路の電流\(i[A]\)は、\(C\)の値\([F]\)に関係する。
時刻\(t=0s\)になった瞬間は、コンデンサは電圧\(v_C=E\)の電源として考えられます。
この時、回路の電流\(i[A]\)は、抵抗のオームの法則のみに従うので、
\(E=iR\)
⇔\(\displaystyle i=\frac{E}{R}\)
となります。したがって、\(C\)の値には無関係ですので誤っています。
以上より、（５）が回答となります。
出典元
令和５年度第三種電気主任技術者試験 理論科目Ａ問題下期問１０
参考書
本ブログの管理人は、電験３種過去問マスタを使って電験３種を取りました。
とても解説が分かり易い参考書なのでお勧めです。
| 電験3種過去問マスタ 理論の20年間 |  |
| 電験3種過去問マスタ 電力の20年間 | |
| 電験3種過去問マスタ 機械の20年間 | |
| 電験3種過去問マスタ 法規の15年間 | |
コメント