概要
コンデンサの直列・並列接続時のそれぞれにおける電荷、電圧を求める問題です。
基本的な問題なので、確実に解答したいところです。
キーワード
コンデンサの直列接続・並列接続、電荷、電圧
問題
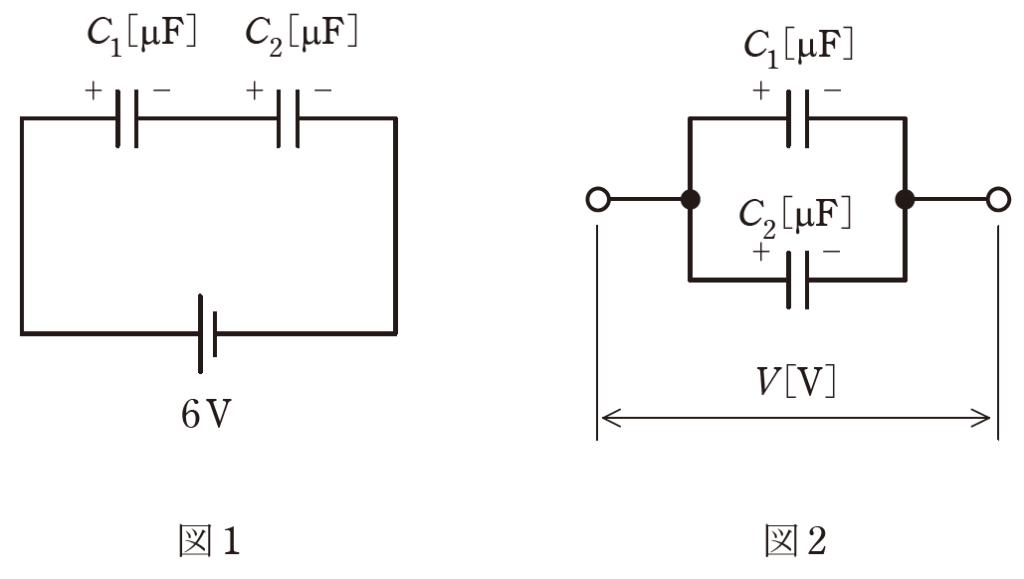
図1に示すように、静電容量\(C_1=4μF\)と\(C_2=2μF\)の二つのコンデンサが直列に接続され、直流電圧\(6V\)で充電されている。
次に電荷が蓄積されたこの二つのコンデンサを直流電源から切り離し、電荷を保持したまま同じ極性の端子同士を図2に示すように並列に接続する。
並列に接続後のコンデンサの端子間電圧の大きさ\(V[V]\)の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(\displaystyle \frac{2}{3}\) (2) \(\displaystyle \frac{4}{3}\) (3) \(\displaystyle \frac{8}{3}\) (4) \(\displaystyle \frac{16}{3}\) (5) \(\displaystyle \frac{32}{3}\)
答え
(3)
解説テキスト リンク
回答解説
解答の流れ
①図1の回路の直列接続されたコンデンサの合成静電容量を求める。
②図1の回路の各コンデンサに充電された電荷を求める。
③図2の回路の並列接続されたコンデンサの合成静電容量を求める。
④図2の回路の電荷を求める。
④\(Q=CV\)の式から、電圧Vを求める。
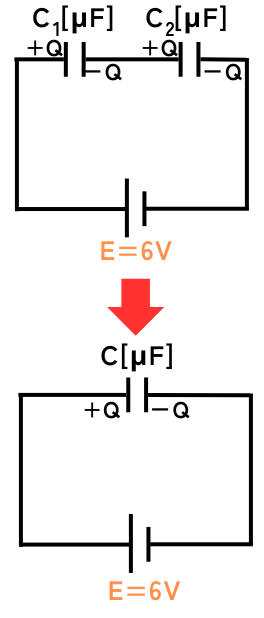
①図1の回路の直列接続されたコンデンサの静電容量を求める。
\(\displaystyle \frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}\)
⇔\(\displaystyle C=\frac{C_1C_2}{C_1+C_2}=\frac{4×10^{-6}・2×10^{-6}}{4×10^{-6}+2×10^{-6}}\)
\(=\frac{4}{3}×10^{-6}F\)
※ \(1μF=1×10^{-6}F\)
②図1の回路の各コンデンサに充電された電荷を求める。
直列に接続されたコンデンサ\(C_1\)と\(C_2\)には、同じ電荷量\(Q[C]\)が充電されます。この電荷量\(Q[C]\)は、次式で求められます。
\(Q=CV=\frac{4}{3}×10^{-6}×6=8×10^{-6}[C]\)
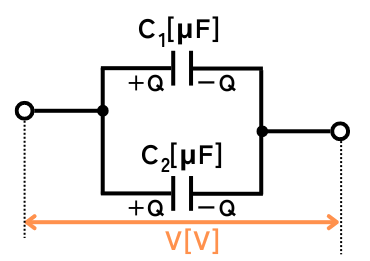
③図2の回路の並列接続されたコンデンサの合成静電容量を求める。
\(C’=C_1+C_2=4μF+2μF=6μF=6×10^{-6}F\)
④図2の回路の電荷を求める。
図1の回路から切り離したコンデンサには、それぞれ\(Q[C]\)の電荷が溜まっています。
同じ極性に並列接続した時、二つの電荷の合計は、
\(Q’=Q+Q=2Q=16×10^{-6}[C]\)となります。
⑤\(Q=CV\)の式から、電圧Vを求める。
③・④で求めた合成静電容量と、電荷を式に代入します。
\(Q’=C’V\)
⇔\(\displaystyle V=\frac{Q’}{C’}=\frac{16×10^{-6}}{6×10^{-6}}=\frac{8}{3}\)
以上より、電圧\(V[V]\)は、\(\displaystyle V=\frac{8}{3}\)です。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和4年度上期 第三種電気主任技術者試験 理論科目A問題問6
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント