難易度
磁界中の導体が動いたときに発生する誘導起電力を求める問題です。
基本的な公式を理解していれば簡単に解ける問題です。
キーワード
誘導起電力、ローレンツ力
問題
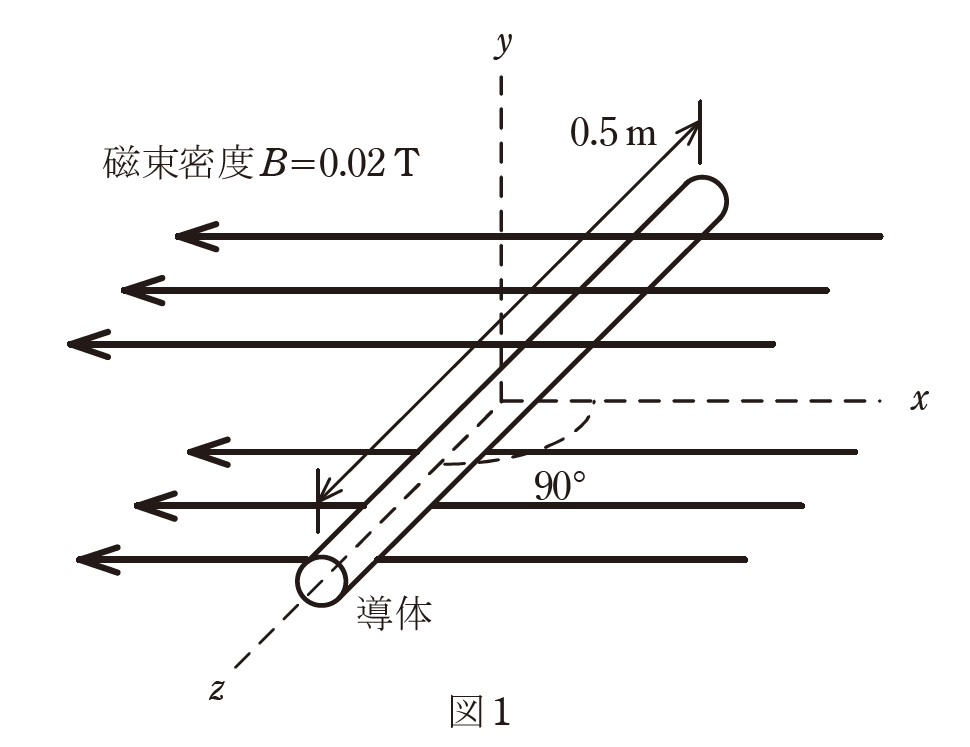
図1のように、磁束密度\(B=0.02 T\) の一様な磁界の中に長さ\(0.5 m\) の直線状導体が磁界の方向と直角に置かれている。
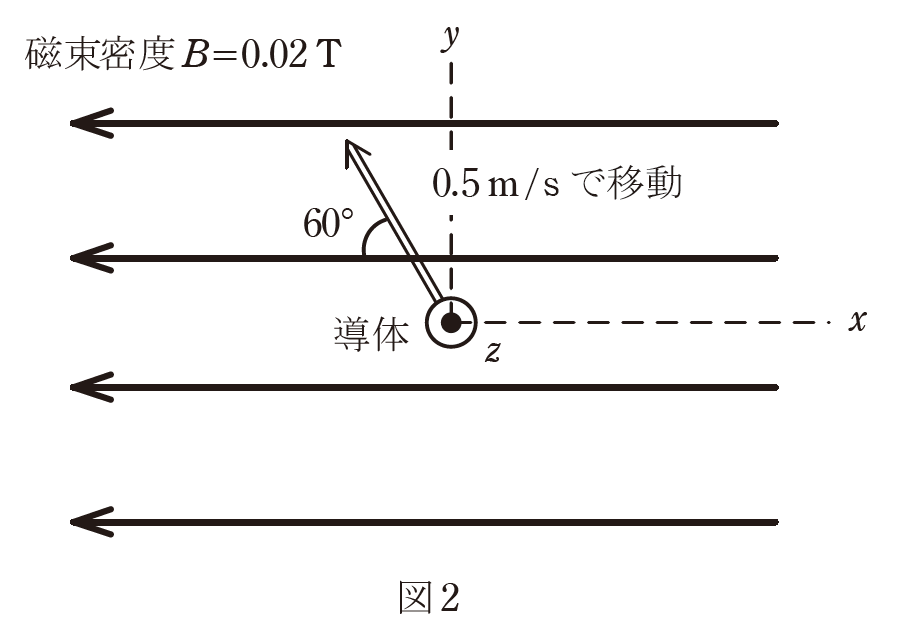
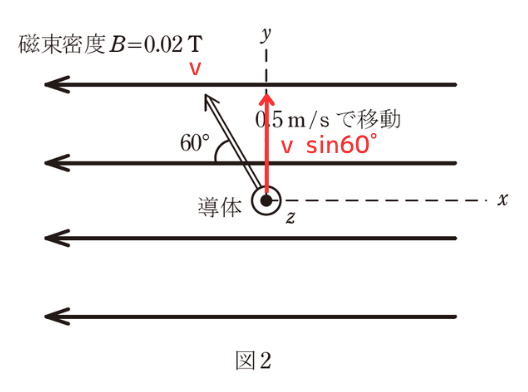
図2 のようにこの導体が磁界と直角を維持しつつ磁界に対して\(60°\)の角度で、二重線の矢印の方向に\(0.5 m/s\) の速さで移動しているとき、導体に生じる誘導起電力\(e\) の値\([mV]\)として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、静止した座標系から見て、ローレンツ力による起電力が発生しているものとする。
(1) 2.5 (2) 3.0 (3) 4.3 (4) 5.0 (5) 8.6
答え
(3)
要点整理
ローレンツ力
磁束密度\(B[T]\)の磁界内を速度\(v[m/s]\)で横切る電荷\(q[C]\)に発生するローレンツ力の大きさの式
\(F=qvBsinθ[N]\)
磁束密度\(B[T]\)の磁界内で、\(l[m]\)の長さの導線に電流\(I[A]\)が流れている時に発生するローレンツ力の大きさの式
\(F=IBlsinθ[N]\)
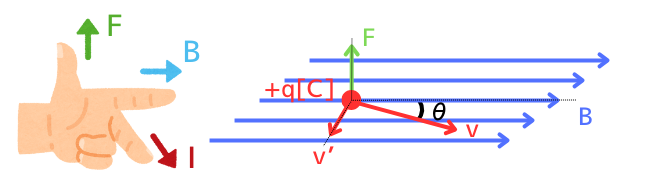
磁束密度\(\vec{B}[T]\)の磁界中を、
電荷\(q[C]\)が速度\(\vec{v}[m/s]\)で動くと、ローレンツ力\(\vec{F}[N]\)を受けます。
ローレンツ力を式に表すと、
\(\vec{F}=q\vec{v}×\vec{B}\)
です。
\(\vec{v}×\vec{B}\)は、電荷の移動速度\(v\)と磁束密度\(B\)の外積を表しますので、\(\vec{v}×\vec{B}\)の大きさは、\(vBsinθ\)です。
従って、ローレンツ力\(F\)の大きさは、
\(F=qvBsinθ\)
となります。
磁束密度\(B[T]\)の磁界中に置かれた導体に、電流\(I[A]\)が流れている時に導体にかかるローレンツ力\(F[N]\)の大きさを求めます。
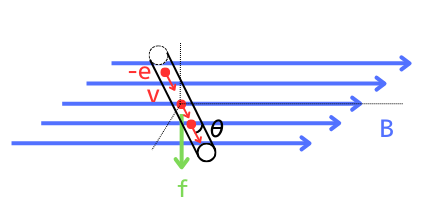
電流は、負電荷である電子\(-e[C]\)が流れているので、1個の電子に発生するローレンツ力は、
\(f=-evBsinθ\) …①
です。
電子は負電荷なので、電子にかかるローレンツ力の向きは、フレミング左手の法則の親指の向きと逆方向です。
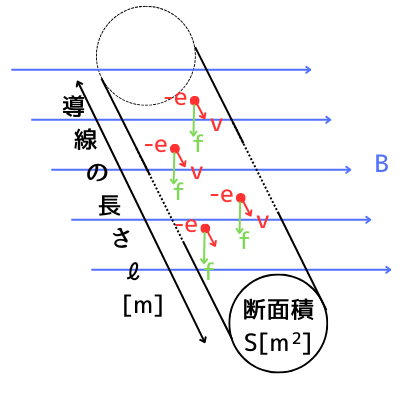
次の条件の導体に流れる電流\(I[A]\)が作るローレンツ力を求めます。
・自由電子数の密度\(n[個/m^3]\)
・断面積\(S[m^2]\)
・長さ\(l[m]\)
導体の中に存在する自由電子の数は、\(nSl[個]\)
導線に発生するローレンツ力は、
\(\begin{eqnarray}
F&=&nSl[個]・f[N/個]\\
&=&-envSBlsinθ[N] …②
\end{eqnarray}\)
となります。
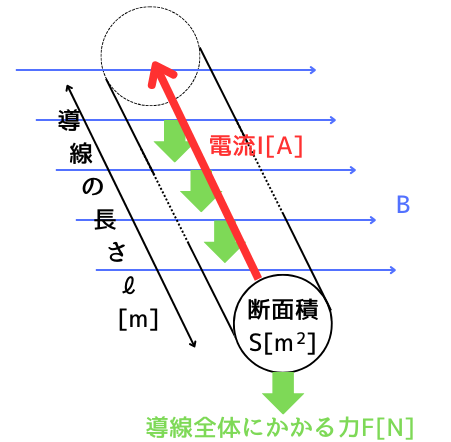
導体の中を流れる自由電子が作り出す電流は、
\(I=-envS[A]\) ………③
ですので、③式を②式に代入すると、
\(F=IBlsinθ[N]\)
ローレンツ力による起電力
ローレンツ力による起電力の式
\(V=vBlsinθ[V]\)
ローレンツ力による起電力の式が、\(V=vBlsinθ\)になる原理を紐解きます。
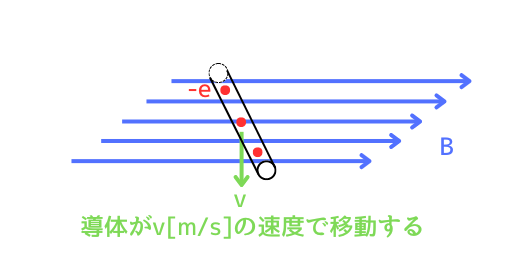
磁束密度\(B[T]\)の磁界中に置かれた導体を
速度\(v[m/s]\)で動かすと、導体内に存在する自由電子も一緒に速度\(v[m/s]\)で動きます。
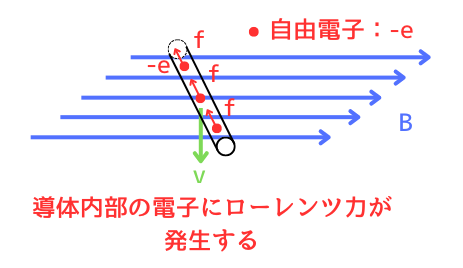
磁界中を自由電子が移動すると、ローレンツ力\(F_L[N]\)が発生します。
ローレンツ力の大きさは、導体の移動の向きと、磁界の向きのなす角をθとしたとき、
\(F_L=-evBsinθ\)
です。
電子は負電荷なので、ローレンツ力の発生する向きは、フレミング左手の法則の中指を速度\(v\)の向きにしたときに親指が向く向きと逆方向です。
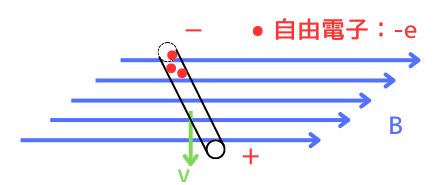
電子が移動して減った側は、電子が不足するので正(+)に帯電します。
電子が集まった側は、負(-)に帯電します。
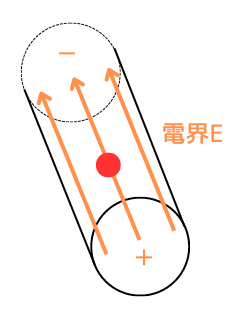
正に帯電した+側と、負に帯電した-側の間に、電界の強さ\(E[V/m]\)の静電界が発生します。
静電界が作り出すクーロン力\(F_C\)と、磁界内の移動によって発生するローレンツ力\(F_L\)が釣り合うまで、電子は-側に移動します。
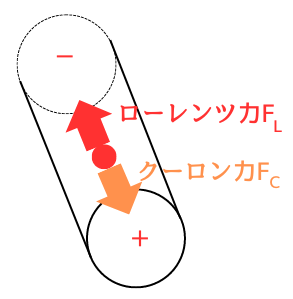
クーロン力の大きさは、\(F_C=-eE\) …①
ローレンツ力の大きさは、\(F_L=-evBsinθ\) …②
ですので、①=②より、
\(F_C=F_L\)
⇔ \(-eE=-evBsinθ\)
⇔ \(E=vBsinθ\) …③
これで、電界の強さ\(E[V/m]\)が求まりました。
平行平板コンデンサのように考えると、電位\(V[V]\)と電界の強さ\(E\)の関係は、
\(V=Ed\) …④
です。
\(d[m]\)は、ここでは導体の長さ\(l[m]\)であるので、\(d=l\)とします。
③式に④式を代入すると、
\(\frac{V}{l}=vBsinθ\)
⇔\(V=vBlsinθ\)
外積
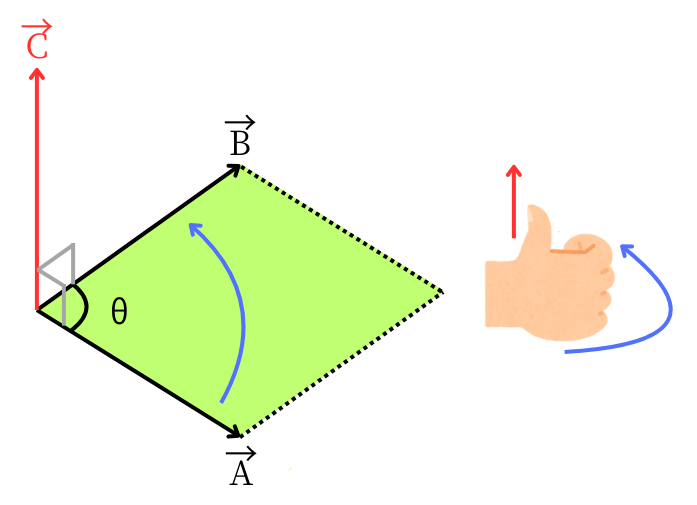
二つのベクトル\(\vec{A}\)、\(\vec{B}\)が作る外積を\(\vec{C}\)とします。
\(\vec{C}\)の向き
\(\vec{A}\)・\(\vec{B}\)の二つと直行した方向です。
そして、\(\vec{A}\)から\(\vec{B}\)に向けて右ねじの法則で回したときに、親指が向く向きと同じです。
\(\vec{C}\)の大きさ
\(\vec{C}\)の大きさは、\(\vec{A}\)と\(\vec{B}\)の作る平行四辺形の面積と同じです。つまり、
\(|C|=|A| |B| sinθ\)
です。大きさだけが欲しい場合は、スカラー表記にしてしまって
\(C=ABsinθ\)
と表すこともあります。
回答解説
ローレンツ力による起電力は、\(V=vBlsinθ[V]\)です。
問題文より下記条件が与えられています。
・磁束密度\(B=0.02[T]\)
・直線状導体の長さ\(l=0.5[m]\)
・磁界の向きと、導体の移動の向きのなす角\(θ=60[°]\)
・導体の移動速度\(v=0.5[m/s]\)
起電力の式を代入すると
\(V=vBlsinθ = 0.5・0.02・0.5・sin60° = 0.00433 = 4.33×10^{-3}[V]\)
したがって、\(V=4.33[mV]\)
以上より、答えは(3) 4.3です。

出典元
一般財団法人 電気技術者試験センター
令和4年度第三種電気主任技術者試験 理論科目A問題上期問4
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント