難易度
点電荷間に働くクーロン力を求める計算問題です。
ベクトル計算を挟むため、少し手順は増えますが、基礎的なレベルなので、確実に回答したい問題です。
キーワード:点電荷、クーロン力、ベクトル計算
問題
真空中において、図に示すように一辺の長さが\(1m\) の正三角形の各頂点に\(1C\)
又は\(-1C\) の点電荷がある。
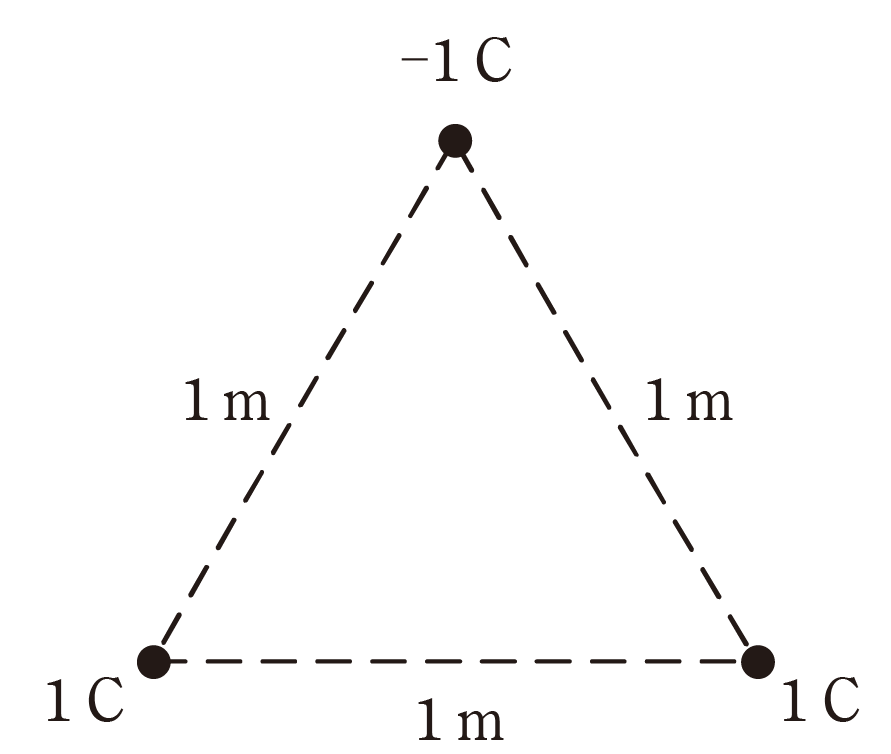
この場合、正の点電荷に働く力の大きさ\(F_1[N]\)と、負の点電荷に働く力の大きさ\(F_2[N]\)の比\(F_2/F_1\) の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(\sqrt{2}\) (2) \(1.5\) (3) \(\sqrt{3}\) (4) \(2\) (5) \(\sqrt{5}\)
答え
(3)
要点整理
クーロン力について
クーロン力の働く向き
・「正電荷-正電荷」「負電荷-負電荷」の符号が同じ時、電荷間に反発力が働く。
・「正電荷-負電荷」の符号が違う時、電荷間に引力が働く。
電界\(E[V/m]\)の大きさ
点電荷\(Q[C]\)が、誘電率\(ε\)の誘電体中に作る電界は、次の式で示されます。
\(\displaystyle E=\frac{Q}{4πεr^2}\)
クーロン力の大きさ
二つの点電荷が\(q[C]\)、\(Q[C]\)としたとき、二つの点電荷には、次の式で示されるクーロン力が働きます。
\(\displaystyle F=\frac{qQ}{4πεr^2}\)
二つの電荷間に働くクーロン力の大きさを求めるため、まず初めに電荷\(+Q[C]\)が作り出す電界の強さ\(E[V/m]\)を求めます。
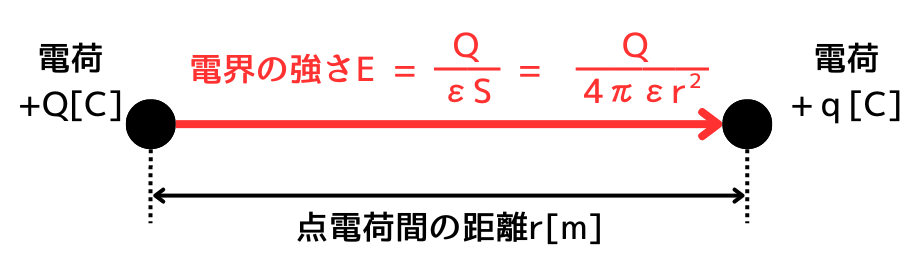
電荷\(Q[C]\)が作り出した電界\(E[V/m]\)は、
\(\displaystyle E=\frac{Q}{εS}\)
です。
面積\(S\)は、球の表面積\(S=4πr^2\)なので、
\(\displaystyle E=\frac{Q}{4πεr^2}\)
と求まります。
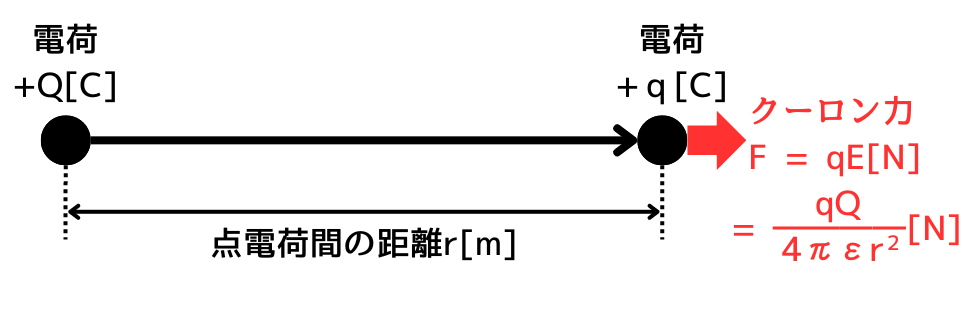
次に、電荷\(q[C]\)に働くクーロン力\(F[N]\)は、
\(\displaystyle F=qE=\frac{qQ}{4πεr^2}\)
と求まります。
ベクトルの合成
同方向のベクトルの合成
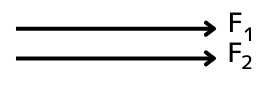
左図のように、同じ方向を向いている力のベクトルが2つあるときのベクトル合成をします。
\(\vec{F_1}\)と、\(\vec{F_2}\)の2つのベクトルがあるとしたとき、合成したベクトルを\(F\)とすると、合成ベクトルの式は、
\(\vec{F}=\vec{F_1}+\vec{F2}\) です。

そして、合成ベクトルの大きさは
\(F=F_1+F_2\)
となります。
方向が違うベクトルの合成
2つのベクトル\(F_1\)と\(F_2\)があり、それぞれの間に\(60°\)の角度があったとします。
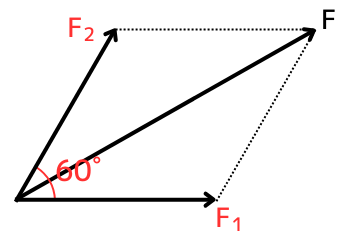
この2つを合成したベクトルを\(F\)とすると、
\(\vec{F}=\vec{F_1}+\vec{F2}\)
です。
次に、ベクトルの大きさを求めます。
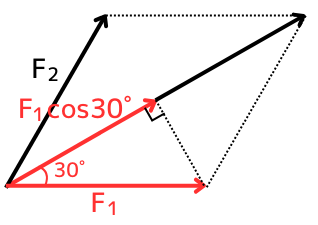
\(\vec{F_1}\)が、\(\vec{F}\)と同じ向きに作るベクトルの大きさは、\(F_1cos30°\)です。
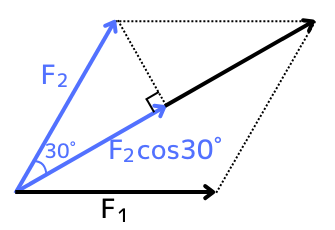
\(\vec{F_2}\)が、\(\vec{F}\)と同じ向きに作るベクトルの大きさは、\(F_2cos30°\)です。
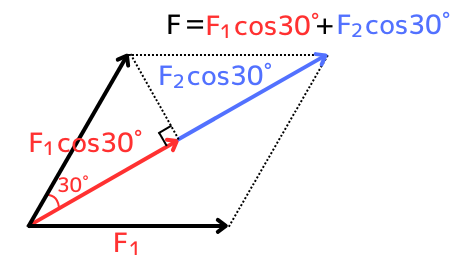
これらを合成すると、\(\vec{F}\)の大きさ\(F\)は、
\(F=F_1cos30°+F_2cos30°\)
です。
回答解説
各電荷間に働くクーロン力を\(F[N]\)とすると、クーロン力の大きさは、\(\displaystyle F=\frac{Q_1Q_2}{4πεr^2}\)です。
本問の電荷は、全て\(1[C]\)なので、\(Q_1=Q_2=1[C]\)
距離は全て\(1[m]\)なので、\(r=1[m]\)
これらを\(F\)の式に代入すると、\(\displaystyle F=\frac{1}{4πε}[N]\)となります。
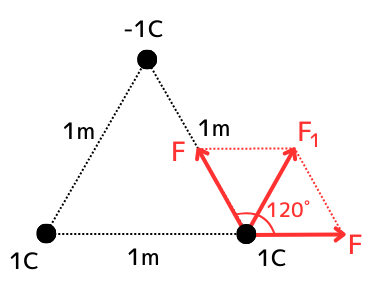
まず初めに、右下の正の電荷に働く力\(F_1[N]\)を求めます。
正電荷-負電荷間は、電荷間に引力が働き、
正電荷-正電荷間は、電荷間に反発力が働きますので、
ベクトル間の角度は、\(120°\)となります。
そして、それぞれのベクトルの大きさは\(F[N]\)です。
これらをまとめると、左図のようになります。
\(F_1\)の大きさを求めると、次のように計算できます。
\(\displaystyle \begin{eqnarray}
F_1&=&Fcos60°+Fcos60°=\frac{1}{2}F+\frac{1}{2}F\\
&=&F=\frac{1}{4πε}
\end{eqnarray}\)
よって、\(\displaystyle F_1=\frac{1}{4πε}\)が求まりました。
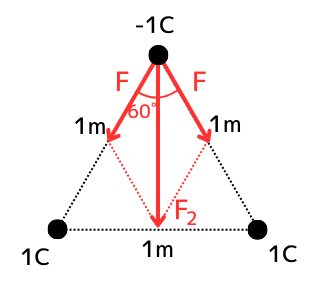
次に、負の電荷に働く力\(F_2[N]\)を求めます。
負電荷に働く力は、正電荷との間に働く引力であり、
ベクトル間の角度は、\(60°\)となります。
そして、それぞれのベクトルの大きさは\(F[N]\)です。
これらをまとめると、左図のようになります。
\(F_2\)の大きさを求めると、次のように計算できます。
\(\displaystyle \begin{eqnarray}
F_2&=&Fcos30°+Fcos30°=\frac{\sqrt{3}}{2}F+\frac{\sqrt{3}}{2}F\\
&=&\sqrt{3}F=\frac{\sqrt{3}}{4πε}
\end{eqnarray}\)
よって、\(\displaystyle F_2=\frac{\sqrt{3}}{4πε}\)が求まりました。
最後に、
\(\displaystyle F_1=\frac{1}{4πε}\) と、\(\displaystyle F_2=\frac{\sqrt{3}}{4πε}\)が求まったので、
\(\displaystyle \frac{F_2}{F_1}=\sqrt{3}\) と、答えが求められます。
以上より、(3)が答えです。
出典元
一般財団法人 電気技術者試験センター
令和4年度第三種電気主任技術者試験 理論科目A問題上期問2
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント