概要
直流回路の計算問題の中でも、難しい部類の問題です。
重要な点は2つほどあります。
・検流計が0Aになるときという条件
・\(R_d\)と\(R_e\)の線が接地されているため、この線が\(0V\)である点
この2つを念頭に、各所の電位を計算していく必要があります。
キーワード
直流回路
問題
図は、抵抗 \(R_{ab}[kΩ]\)のすべり抵抗器、抵抗\(R_d[kΩ]\)、抵抗\(R_e[kΩ]\)と直流電圧
\(E_s=12V\)の電源を用いて、端子 H、G 間に接続した未知の直流電圧[V]を測るための回路である。
次の(a)及び(b)の問に答えよ。
ただし、端子G を電位の基準(\(0 V\))とする。
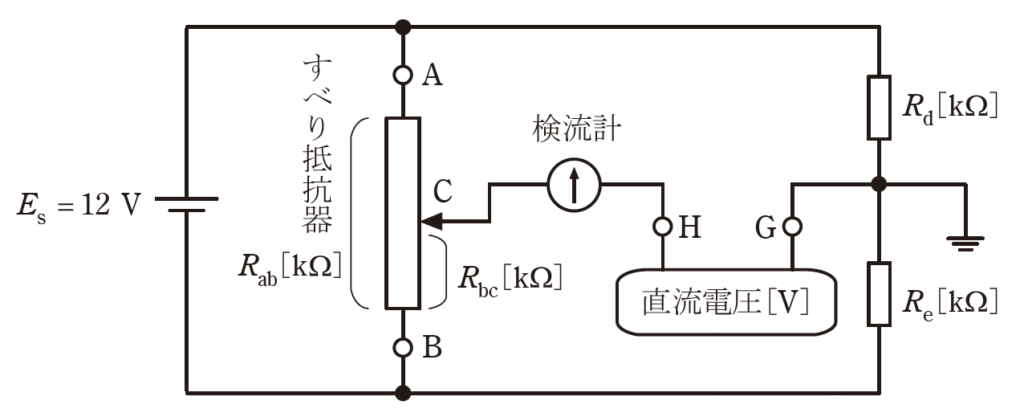
(a) 抵抗 \(R_d=5[kΩ]\) 、抵抗 \(R_e=5[kΩ]\) として、直流電圧 3 V の電源の正極を端子 H に、負極を端子 G に接続した。
すべり抵抗器の接触子 C の位置を調整して検流計の電流を零にしたところ、すべり抵抗器の端子 B と接触子 C 間の抵抗 \(R_{bc}[kΩ]\) となった。すべり抵抗器の抵抗 \(R_{ab}[kΩ]\) の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 18 (2) 24 (3) 36 (4) 42 (5) 50
(b) 次に、直流電圧3 V の電源を取り外し、未知の直流電圧\(E_x[V]\)の電源を端子H、G 間に接続した。ただし、端子G から見た端子H の電圧を\(E_x[V]\)とする。
抵抗\(R_d=2[kΩ]\) 、抵抗\(R_e=22[kΩ]\) としてすべり抵抗器の接触子 C の位置を調整し、すべり抵抗器の端子B と接触子C 間の抵抗\(R_{bc}=12[kΩ]\) としたときに、検流計の電流が零となった。このときの\(E_x[V]\)の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) -5 (2) -3 (3) 0 (4) 3 (5) 5
答え
(a)(2)
(b)(1)
解説テキスト リンク
回答解説
(a)の解答の流れ
①抵抗\(R_d\)、\(R_e\)に流れる電流を求める
②端子Bの電位\(V_B\)を求める
③分圧の法則から\(R_{ab}\)を求める
①抵抗\(R_d\)、\(R_e\)に流れる電流を求める
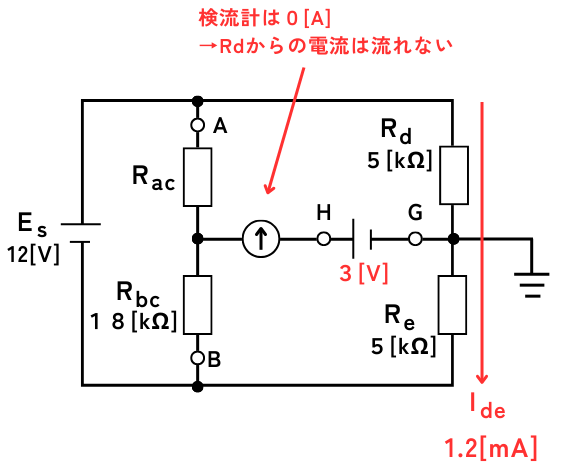
抵抗\(R_d\)、\(R_e\)に流れる電流を\(I_{de}\)としたとき、オームの法則から、
\(\displaystyle I_{de}=\frac{E_s}{R_d+R_e}=1.2[mA]\)
なお、次の2つの理由により、抵抗\(R_d\)を流れた電流は、\(R_e\)に全て流れ込みます。
・検流計が\(0[A]\)が条件であるため、端子Gには電流は流れません。
・接地からは直流電源\(E_s\)と閉回路を構成しないため、接地には電流が流れません。
②端子Bの電位\(V_B\)を求める
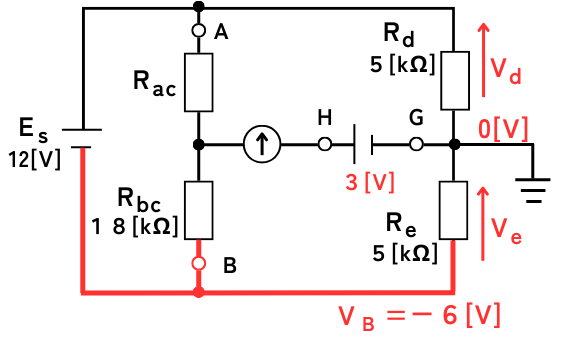
\(I_{de}=1.2[mA]\)から、抵抗\(R_d\)、\(R_e\)の端子間の電位差を求めると
\(V_d=6[V]\)
\(V_e=6[V]\)
端子Gの電位は接地されていて\(0[V]\)であるため、端子Bの電位\(V_B\)は、
\(V_B=-6[V]\)
③分圧の法則から\(R_{ab}\)を求める
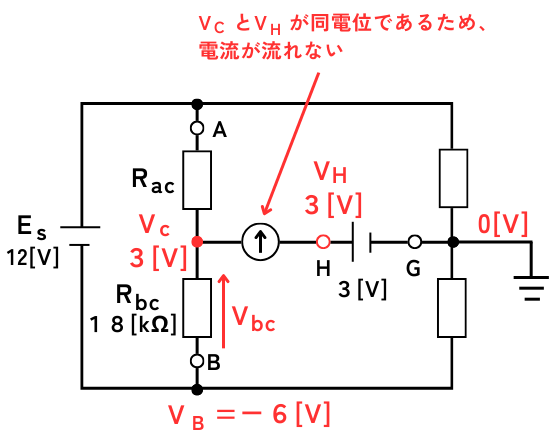
\(3[V]\)の直流電圧源の+端子である端子Hと、すべり抵抗器のC点の電位が同じときに、検流計は0Aを指し示すので、
C点の電位\(V_C=3V\)であることがわかります。
\(V_B=-6V\)なので、抵抗\(R_{bc}\)の電位差\(V_{BC}=3-(-6)=9V\)です。
分圧の法則から、
\(\displaystyle V_{BC}=\frac{R_{bc}}{R_{ac}+R_{bc}}E_s=\frac{R_{bc}}{R_{ab}}E_s\)
⇔ \(\displaystyle 9=\frac{18×10^3}{R_{ab}}・12\)
⇔ \(\displaystyle R_{ab}=\frac{12}{9}・18×10^3=24kΩ\)
以上より、(a)問題の答えは(2)24 が答えです。
(b)の解答の流れ
①抵抗\(R_d\)、\(R_e\)に流れる電流を求める
②端子Bの電位\(V_B\)を求める
③分圧の法則から\(V_C\)を求める
①抵抗\(R_d\)、\(R_e\)に流れる電流を求める
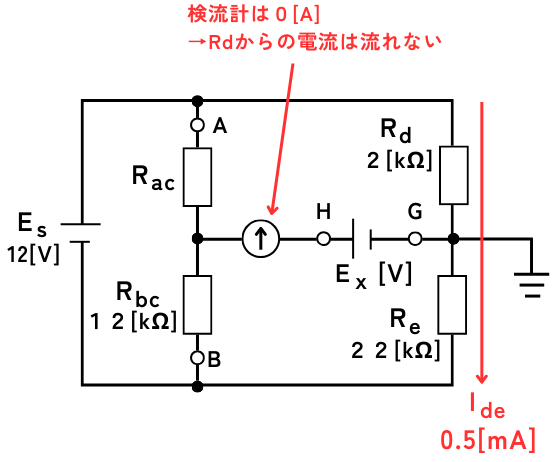
抵抗\(R_d\)、\(R_e\)に流れる電流を\(I_{de}\)としたとき、オームの法則から、
\(\displaystyle I_{de}=\frac{E_s}{R_d+R_e}=0.5[mA]\)
②端子Bの電位\(V_B\)を求める
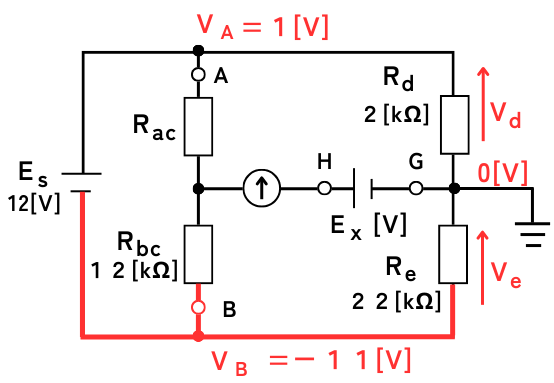
\(I_{de}=0.5[mA]\)から、抵抗\(R_d\)、\(R_e\)の端子間の電位差を求めると
\(V_d=1[V]\)
\(V_e=11[V]\)
端子Gの電位は接地されていて\(0[V]\)であるため、
端子Aの電位\(V_A\)は、\(V_A=1[V]\)
端子Bの電位\(V_B\)は、\(V_B=-11[V]\)
③分圧の法則から\(V_C\)を求める
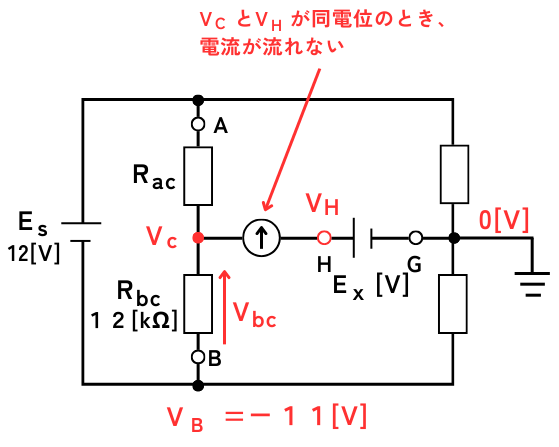
下記4つの条件から、\(R_{bc}\)の電位差\(V_{bc}\)を求めます。
②から、\(V_B=-11V\)
問題文から、\(E_s=12V\)
(a)問題から、\(R_{ab}=24kΩ\)
問題文から、\(R_{bc}=12kΩ\)
\(\displaystyle V_{bc}=\frac{R_{bc}}{R_{ab}}E_s=\frac{12}{24}・12=6V\)
接触子Cの電位\(V_C=V_{bc}+V_B=6+(-11)=-5\)
\(E_x[V]\)の直流電圧源の+端子である端子Hと、すべり抵抗器のC点の電位が同じときに、検流計は0Aを指し示すので、\(E_x=V_H=V_C=-5V\)です。
以上より、(b)問題の答えは(1)-5 が答えです。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和4年度上期 第三種電気主任技術者試験 理論科目B問題問16
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント