概要
計測器の測定方法に関する論説問題です。
よく出題される範囲なので、確実な解答ができるようになっておきたい問題です。
キーワード
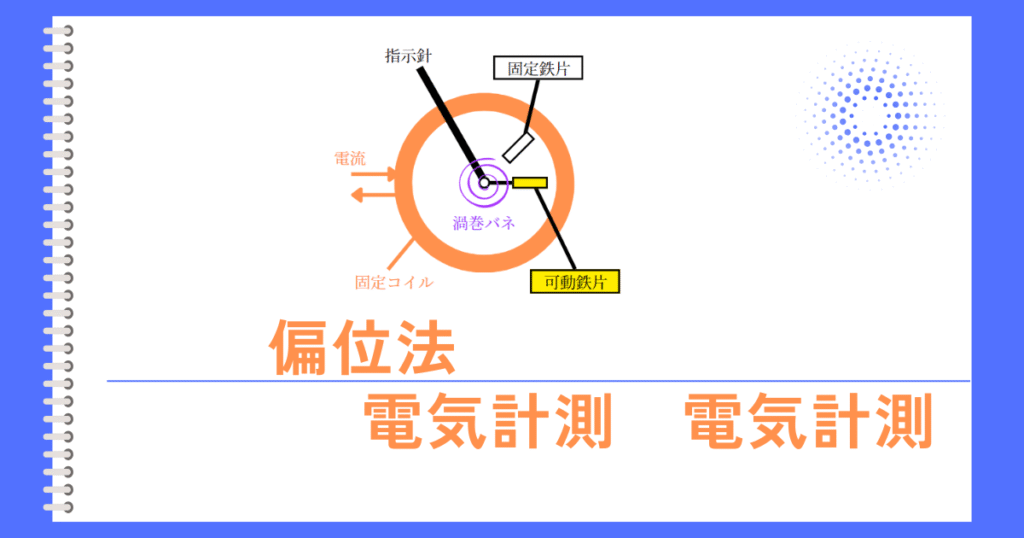
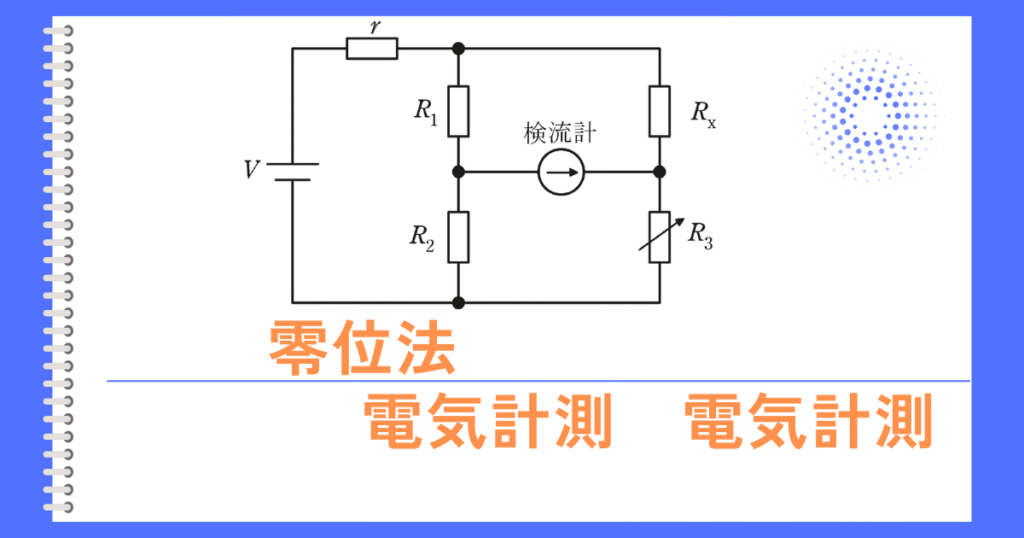
偏位法、零位法
問題
電気に関する物理量の測定に用いる方法には各種あるが、指示計器のように測定量を指針の振れの大きさに変えて、その指示から測定量を知る方法を \(\fbox{(ア)}\) 法という。
これに比較して精密な測定を行う場合に用いられている \(\fbox{(イ)}\) 法は、測定量と同種類で大きさを調整できる既知量を別に用意し、既知量を測定量に平衡させて、そのときの既知量の大きさから測定量を知る方法である。
\(\fbox{(イ)}\) 法を用いた測定器の例としては、 \(\fbox{(ウ)}\) がある。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | |
|---|---|---|---|
| (1) | 偏位 | 零位 | ホイートストンブリッジ |
| (2) | 間接 | 差動 | 誘導形電力量計 |
| (3) | 間接 | 零位 | ホイートストンブリッジ |
| (4) | 偏位 | 差動 | 誘導形電力量計 |
| (5) | 偏位 | 零位 | 誘導形電力量計 |
答え
(1)
解説テキスト リンク
回答解説
\(\fbox{(ア)}\) 法
指示計器のように測定量を指針の振れの大きさに変えて、その指示から測定量を知る方法は偏位法です。
指示値を読むだけで簡単という長所はありますが、精度が悪いという短所があります。
精度が悪い理由は、測定量(回路に流れる電流)を指示針を振るためのエネルギーとして変換するためです。変換の結果、計器が回路から受取った分だけエネルギーの分だけ誤差を発生させます。そのため、精度が悪くなってしまうわけです。
\(\fbox{(イ)}\) 法
精密な測定を行う場合に用いられている 零位法は、測定量と同種類で大きさを調整できる既知量を別に用意し、既知量を測定量に平衡させて、そのときの既知量の大きさから測定量を知る方法です。
平衡するまで調整する手間があるものの、平衡した測定回路は測定対象からエネルギーを取ることなく測定ができるため、測定対象に与える影響が小さく精度良く測定できます。
\(\fbox{(ウ)}\)
零位法の例は、ホイートストンブリッジ回路です。
誘導形電力量計は、偏位法の計器です。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和4年度上期 第三種電気主任技術者試験 理論科目A問題問14
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント