【電験三種：理論】令和４年度下期　問６

概要

直流回路に直列・並列接続されたコンデンサの容量、エネルギー、電荷量の問題です。
基本問題なので、確実な回答が求められます。

キーワード
コンデンサ、直列接続、並列接続、静電容量、静電エネルギー

　

問題

電圧$E [V]$の直流電源と静電容量$C [F]$の二つのコンデンサを接続した図１、図２ のような二つの回路に関して、誤っているものを次の(1)～(5)のうちから一つ選べ。

　

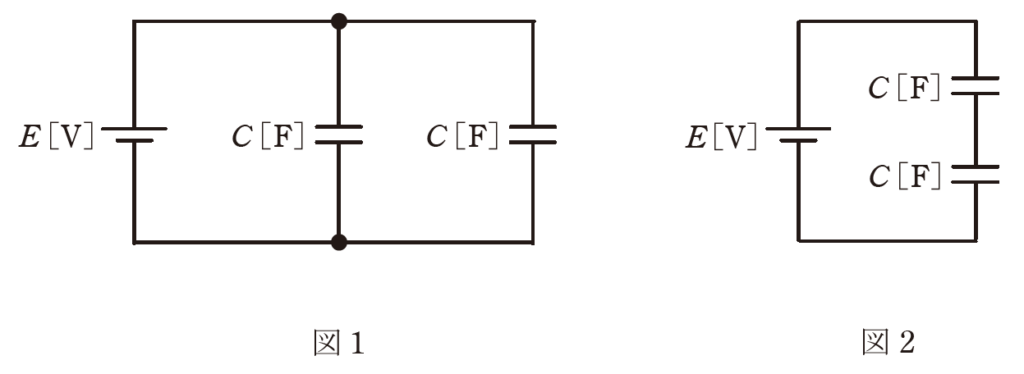
(1) 図１の回路のコンデンサの合成静電容量は、図２の回路の４倍である。

(2) コンデンサ全体に蓄えられる電界のエネルギーは、図１の回路の方が図２の回路より大きい。

(3) 図２の回路に、さらに静電容量C [F]のコンデンサを直列に二つ追加して、四つのコンデンサが直列になるようにすると、コンデンサ全体に蓄えられる電界のエネルギーが図１と等しくなる。

(4) 図２の回路の電源電圧を２倍にすると、コンデンサ全体に蓄えられる電界のエネルギーが図１の回路と等しくなる。

(5) 図１のコンデンサ一つ当たりに蓄えられる電荷は、図２のコンデンサ一つ当たりに蓄えられる電荷の２倍である。

　

　

　

答え

(３)

解説テキスト　リンク

　

回答解説

問題文に出てくる各回路の合成静電容量と、静電エネルギーを求めます
①図１のコンデンサの合成静電容量$C_p$
　$C_p=C+C=2C[F]$

②図１のコンデンサの静電エネルギー$U_p$
　$\displaystyle U_p=\frac{1}{2}C_pE^2=CE^2[J]$

③図２のコンデンサの合成静電容量$C_s$
　$\displaystyle \frac{1}{C_s}=\frac{1}{C}+\frac{1}{C}=\frac{2}{C}[F]$　⇔　$\displaystyle C_s=\frac{1}{2}C[F]$

④図２のコンデンサの静電エネルギー$U_s$
　$\displaystyle U_s=\frac{1}{2}C_sE^2=\frac{1}{4}CE^2[J]$

⑤４つのコンデンサを直列接続したときの合成静電容量$C_{s4}$
　$\displaystyle \frac{1}{C_s}=\frac{1}{C}+\frac{1}{C}+\frac{1}{C}+\frac{1}{C}=\frac{4}{C}[F]$
　⇔　$\displaystyle C_s=\frac{1}{4}C[F]$

⑥４つのコンデンサを直列接続したときの静電エネルギー$U_{s4}$
　$\displaystyle U_{s4}=\frac{1}{2}C_{s4}E^2=\frac{1}{8}CE^2[J]$

(1) 図１の回路のコンデンサの合成静電容量は、図２の回路の４倍である。
①の$C_p=2C$と、③の$\displaystyle C_s=\frac{1}{2}C$の比較です。
$\displaystyle \frac{C_p}{C_s}=\frac{2C}{\frac{1}{2}C}=4$

以上より、図１の回路のコンデンサの合成静電容量は、図２の回路の４倍で正しいです。

---

(2) コンデンサ全体に蓄えられる電界のエネルギーは、図１の回路の方が図２の回路より大きい。
②の$U_p=CE^2$と、④の$\displaystyle U_s=\frac{1}{4}CE^2$の比較です。
$\displaystyle \frac{U_p}{U_s}=\frac{CE^2}{\frac{1}{4}CE^2}=4$

以上より、コンデンサ全体に蓄えられる電界のエネルギーは、図１の回路の方が図２の回路より大きいため正しいです。

(3) 図２の回路に、さらに静電容量C [F]のコンデンサを直列に二つ追加して、四つのコンデンサが直列になるようにすると、コンデンサ全体に蓄えられる電界のエネルギーが図１と等しくなる。
②の$U_p=CE^2$と、⑥の$\displaystyle U_{s4}=\frac{1}{8}CE^2$の比較です。
$\displaystyle \frac{U_{s4}}{U_p}=\frac{\frac{1}{8}CE^2}{CE^2}=\frac{1}{8}$

以上より、四つのコンデンサが直列になるようにしたときのエネルギーは、図１の$\frac{1}{8}$倍となるので間違いです。

(4) 図２の回路の電源電圧を２倍にすると、コンデンサ全体に蓄えられる電界のエネルギーが図１の回路と等しくなる。
電源電圧を２倍にした時の静電エネルギーを$U’_s$とすると、
$\displaystyle U’_s=\frac{1}{2}C_s(2E)^2=CE^2$

②の$\displaystyle U_p=CE^2$と比較をします。
$\displaystyle \frac{U’_s}{U_p}=\frac{CE^2}{CE^2}=1$

以上より、$U’_s=U_p$となって等しいので正しいです。

(5) 図１のコンデンサ一つ当たりに蓄えられる電荷は、図２のコンデンサ一つ当たりに蓄えられる電荷の２倍である。
図１のコンデンサ一つの静電容量は$C$、コンデンサにかかる電圧は$E$なので、
コンデンサ一つ当たりに蓄えられる電荷$Q_{p1}$は、$Q_{p1}=CE$

図２のコンデンサ一つの静電容量は$C$、コンデンサにかかる電圧は$\frac{1}{2}E$なので、
コンデンサ一つ当たりに蓄えられる電荷$Q_{s1}$は、$Q_{s1}=\frac{1}{2}CE$

比較をすると、
$\displaystyle \frac{Q_{p1}}{Q_{s1}}=\frac{CE}{\frac{1}{2}CE}=2$

以上より、図１のコンデンサ一つ当たりに蓄えられる電荷は、図２のコンデンサ一つ当たりに蓄えられる電荷の２倍で正しいです。

　

　

　

出典元

一般財団法人電気技術者試験センター　（https://www.shiken.or.jp/index.html）
令和４年度下期　第三種電気主任技術者試験　理論科目Ａ問題問６

参考書