難易度
磁力線に関する基礎的な論説問題です。
磁力線に関する基本的な性質と、アンペールの法則を理解しておいた方が良いでしょう。
問題
無限に長い直線状導体に直流電流を流すと、導体の周りに磁界が生じる。
この磁界中に小磁針を置くと、小磁針のアは磁界の向きを指して静止する。
そこで、小磁針を磁界の向きに沿って少しずつ動かしていくと、導体を中心とした イの線が得られる。
この線に沿って磁界の向きに矢印をつけたものをウという。
また,磁界の強さを調べてみると,電流の大きさに比例し,導体からのエに反比例している。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | N極 | 放射状 | 電気力線 | 距離の2 乗 |
| (2) | N極 | 同心円状 | 電気力線 | 距離の2 乗 |
| (3) | S極 | 放射状 | 磁力線 | 距離 |
| (4) | N極 | 同心円状 | 磁力線 | 距離 |
| (5) | S極 | 同心円状 | 磁力線 | 距離の2 乗 |
答え
(4)
要点整理
電流と磁界の向き
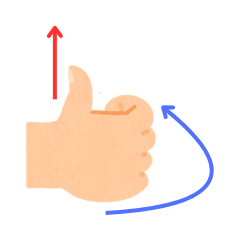
直線状導体に電流を流すと、電流を中心に同心円状の磁界が発生します。その向きは、右手で親指を立てたとき、
・電流:親指の向き
・磁界:他の指の向き
となります。
これを右ねじの法則と呼びます。
方位磁石のN極は、磁界の向きを指します。
アンペールの法則

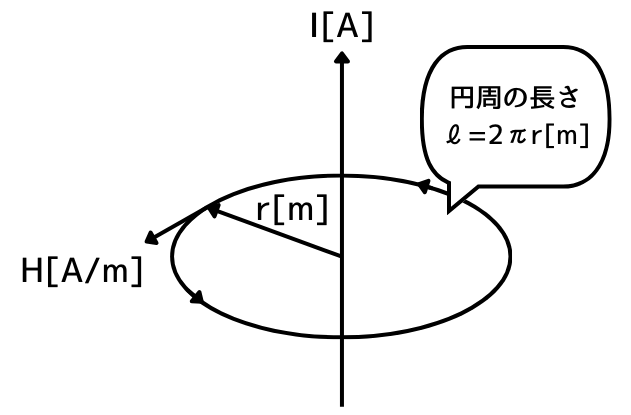
電流が作る磁界中で、磁界の強さが等しい所をたどって1周したときの磁路の長さ\(l=2\pi r[m]\)と、磁界の強さ\(H[A/m]\)の積が、電流\(I[A]\)に等しいという法則です。
式に示すと、
\( \displaystyle I=\oint_C Hdl\) \(=Hl=H\times 2\pi r \)
となります。変形すると、
\(\displaystyle H=\frac{I}{2\pi r}[A/m]\)
となります。
磁力線の性質
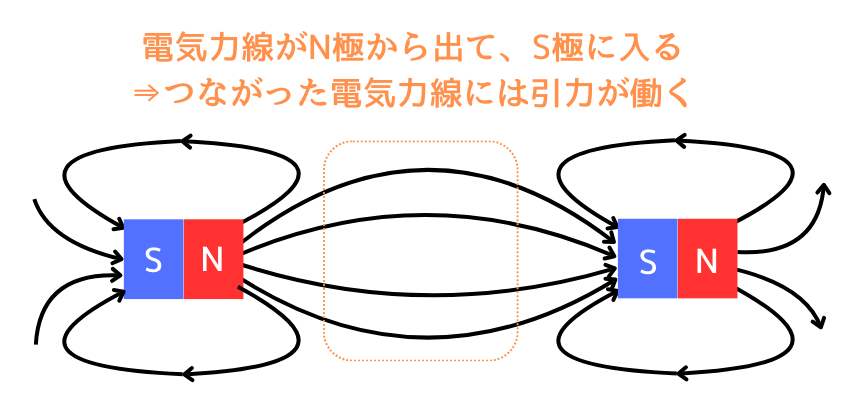
①・②の性質の図
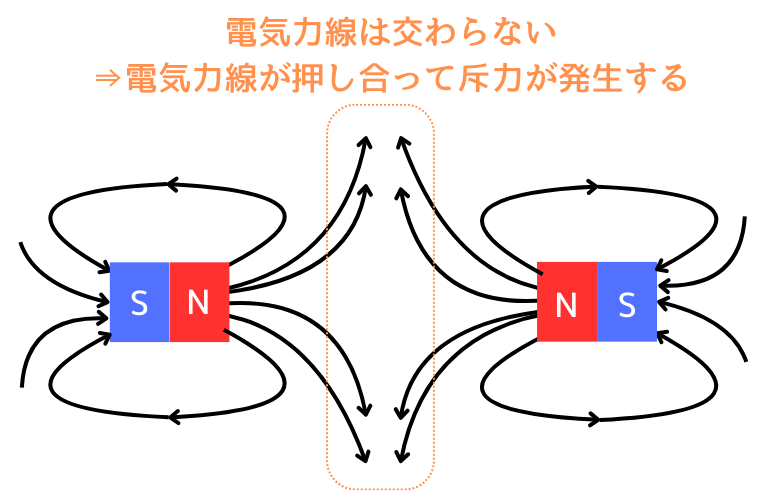
④・⑤の性質の図
磁力線の性質をまとめると以下の通りです。
① N極(+磁荷)から発生し、S極(-磁荷)に吸収される。
② 磁力線でつながった磁荷の間には、引力が働く
(つながった本数が多い程大きな力が働く)
③ 磁荷の無い所から発生したり消滅したりしない。
④ 磁力線は交わらない。
⑤ 磁力線は交わらないため、同じ符号の磁荷の間には斥力が働く
⑥ 磁力線は分岐しない。
⑦ 磁力線は途切れない。
⑧ 磁荷の大きさと、磁力線の本数は比例する。
回答解説
ア
小磁針はN極の向きを指します。
イ・ウ
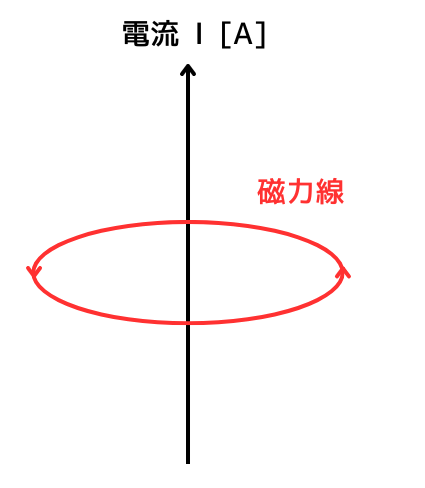
電流と磁界の向きの要点整理のとおり、直線状導体に電流を流すと、導体を中心とした同心円状の磁界が発生します。
同心円状の磁界に線を引き、矢印をつけたものを磁力線と呼びます。
エ
アンペールの法則から、電流\(I[A]\)と磁界の強さ\(H[A/m]\)の関係は、
\( \displaystyle I=\oint_C Hdl\) \(=Hl=H\times 2\pi r \)
⇔\(\displaystyle H=\frac{I}{2\pi r}[A/m]\)
したがって、磁界の強さ\(H\)は、
電流\(I[A]\)に比例し、導体からの距離\(r[m]\)に反比例しています。
以上より、(4)が答えです。
出典元
一般財団法人 電気技術者試験センター
令和4年度第三種電気主任技術者試験 理論科目A問題下期問3
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント