概要
発振回路の論説問題です。
電験三種を学ぶ段階では、発振条件については勉強している人は多くはないかと思います。
キーワード
発振回路、発振条件
問題
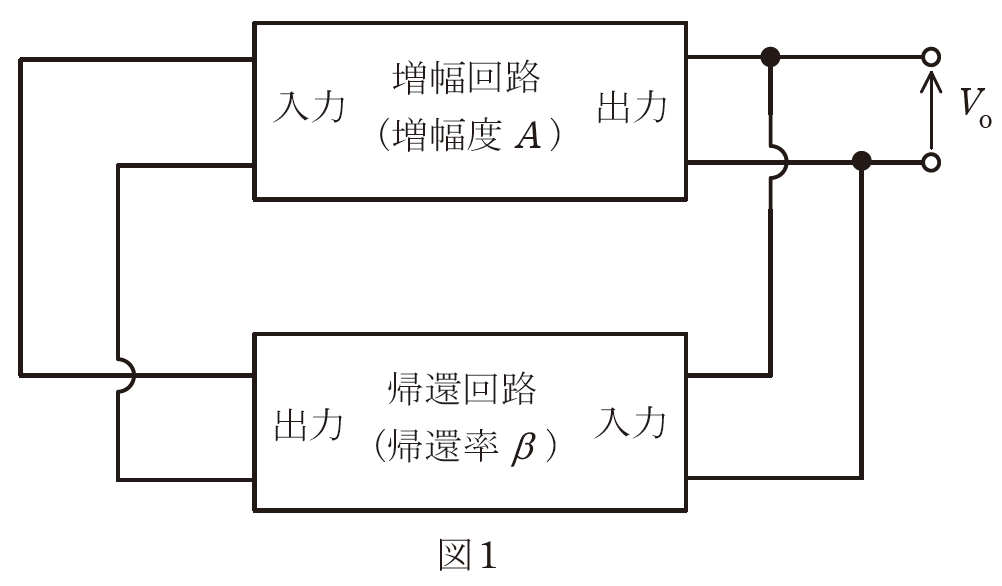
図1は、正弦波を出力しているある発振回路の構造を示している。
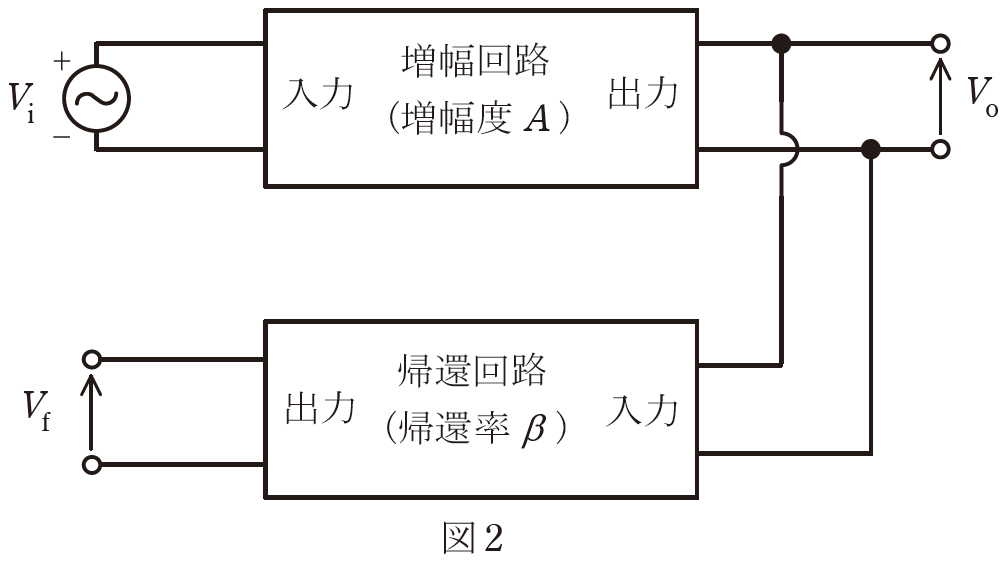
この発振回路の帰還回路の出力端子と増幅回路の入力端子との接続を切り離し、図2のように適当な周波数の正弦波\(V_i\) を増幅回路に入力すると、次の二つの条件が同時に満たされている。
1.増幅回路の入力電圧\(V_i\) と帰還回路の出力電圧\(V_f\) が \(\fbox{(ア)}\) である。
2.増幅回路の増幅度\(\left| \frac{V_o}{V_i} \right|\)を\(A\)、帰還回路の帰還率\(\left| \frac{V_f}{V_o} \right|\)を\(β\)と表すとき、 \(\fbox{(イ)}\) である。
図1で示される発振回路は、条件1より \(\fbox{(ウ)}\) 回路である。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | |
|---|---|---|---|
| (1) | 同相 | A ≧1 | 正帰還 |
| (2) | 逆相 | A ≧1 | 負帰還 |
| (3) | 同相 | A <1 | 負帰還 |
| (4) | 逆相 | A ≧1 | 正帰還 |
| (5) | 同相 | A <1 | 正帰還 |
答え
(1)
解説テキスト リンク
回答解説
1.増幅回路の入力電圧\(V_i\) と帰還回路の出力電圧\(V_f\) が \(\fbox{(ア)}\) である。
図1の回路は出力\(V_o\)に帰還率\(β\)倍した信号を同相で入力していますので、\(\fbox{(ア)}\) は同相です。
同相信号を増幅回路の入力に戻していることから、\(\fbox{(ウ)}\) は正帰還回路です。
2.増幅回路の増幅度\(\left| \frac{V_o}{V_i} \right|\)を\(A\)、帰還回路の帰還率\(\left| \frac{V_f}{V_o} \right|\)を\(β\)と表すとき、 \(\fbox{(イ)}\) である。

出力\(V_o\)が帰還率\(β\)倍の帰還回路で入力に戻された後、増幅度\(A\)倍の増幅回路で戻って来たとき、戻って来た出力信号\(V_o\)は、\(Aβ\)倍されます。
この\(Aβ\)をループ利得と呼びます。
ループ利得\(Aβ=1\)のとき、出力信号は減衰も増幅もしませんので、信号はループし続けます。
ループ利得\(Aβ>1\)のとき、出力信号は飽和するまで増幅します。飽和した後は\(V_o=V_i\)となるため、\(Aβ=1\)のときと同じ状態となります。
信号がループし続けているときに発振するので、\(Aβ≧1\)が発振条件であることが分かります。
この\(Aβ≧1\)の条件は、振幅条件と呼びます。
帰還率\(β\)は1以下であるため、この振幅条件を満たすためには\(A≧1\)である必要があります。
したがって、\(\fbox{(イ)}\) は\(A≧1\)です。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和4年度上期 第三種電気主任技術者試験 理論科目A問題問13
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント