概要
ローレンツとフレミング左手の法則の計算問題です。
基礎的な問題なので確実に回答したい問題です。
考える電荷が電子であり、電子は負電荷であることを考慮しなければならないので注意しましょう。
キーワード
ローレンツ力、フレミング左手の法則、電子(負電荷)
問題
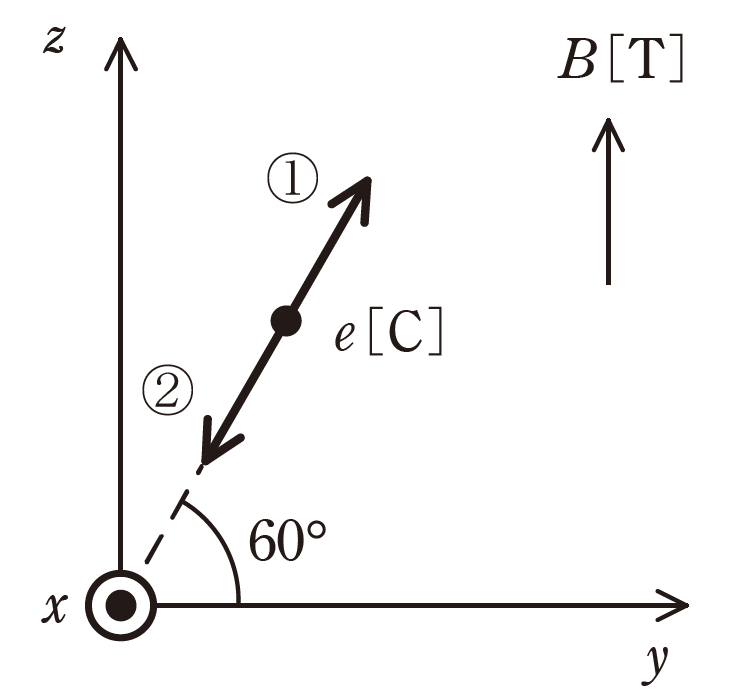
図のように、z 軸の正の向きに磁束密度 \(B=1.0×10^{-3} T\) の平等磁界が存在する真空の空間において、電気量\(e=4.0×10^{-6} C\)の荷電粒子が yz 平面上を y 軸から60°の角度で①又は②の向きに速さv[m/s]で発射された。
この瞬間、荷電粒子に働くローレンツ力\(F\)の大きさは\(1.0×10^{-8} N\) 、その向きはx軸の正の向きであった。
荷電粒子の速さ\(v\) に最も近い値 [m/s] とその向きの組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、重力の影響は無視できるものとする。
図中の ◉ は、紙面に対して垂直かつ手前の向きを表す。
| 速さ\(v\) | 向き | |
|---|---|---|
| (1) | 2.5 | ① |
| (2) | 2.9 | ① |
| (3) | 5.0 | ① |
| (4) | 2.9 | ② |
| (5) | 5.0 | ② |
答え
(5)
解説テキスト リンク
回答解説
解答の流れ
①フレミング左手の法則から、電子の移動の向きを考える(負電荷に注意)
②速度\(v\)のy軸成分だけを取り出す
③ローレンツ力の大きさの式\(F=qv_yB\)から速度\(v\)を求める
①フレミング左手の法則から、電子の移動の向きを考える(負電荷に注意)
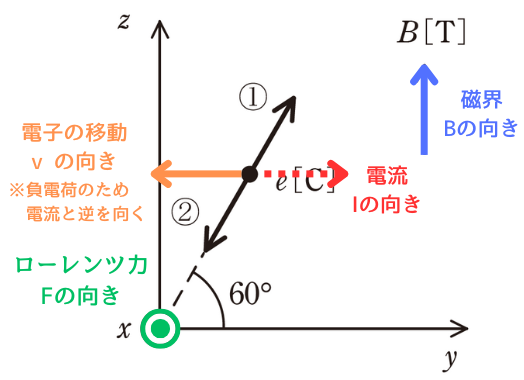
・ローレンツ力の向きはx軸の正
・平等磁界の向きはz軸の正
であることが問題文で定められているため、フレミング左手の法則から電流の向きはy軸の正であることが分かります。
電子は、負電荷であるため、電流の向きと逆向きに移動しますので、電子の移動の向きはy軸の負です。
したがって、電子の発射の向きは、②の向きに速さv[m/s]で発射されたと導き出せます。
②速度\(v\)のy軸成分だけを取り出す
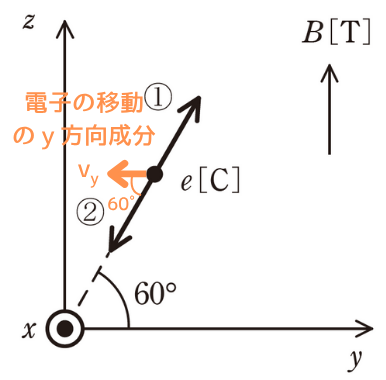
電子の移動の向きは②の矢印の向きです。
ローレンツ力として働く
③ローレンツ力の大きさの式\(F=qv_yB\)から速度\(v\)を求める
問題文から、\(F=1.0×10^{-8} N\)、\(q=e=4.0×10^{-6} C\)、\(B=1.0×10^{-3} T\)
\(F=qv_yB=qvBcos60°=\frac{1}{2}qvB\)
⇔ \(\displaystyle v=\frac{2F}{qB}=\frac{2・1.0×10^{-8}}{4.0×10^{-6}・1.0×10^{-3}}=5.0[m/s]\)
以上より、(5)\(v=5.0\)、向きは② が答えです。
ローレンツ力の式\(F=qvBsinθ\)を適用する場合
ローレンツ力は、ベクトルで表すと\(\vec{F}=q \vec{v}×\vec{B}\)です。
\(\vec{F}\)は、\(\vec{v}\)と\(\vec{B}\)の外積であるため、
力\(F\)の大きさは、\(F=qvBsinθ\)と表されます。
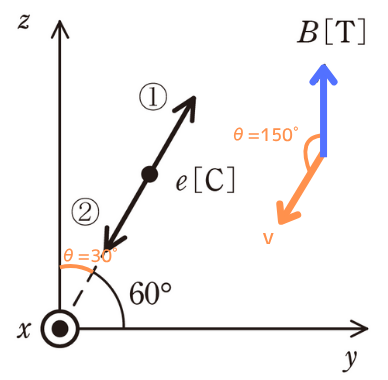
この\(sinθ\)を直接適用したい場合は、\(\vec{v}\)と\(\vec{B}\)のなす角が\(θ\)であるため、その角度は\(θ=150°\)です。
\(\displaystyle sin150°=\frac{1}{2}\)なので、これを適用すると、
\(\displaystyle v=\frac{F}{qBsin150°}=5.0[m/s]\)
と求めることができます。
以上のことから、問題文で与えられている角度\(60°\)をそのままローレンツ力の式に適用してしまうと、間違いになるので注意が必要です。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和4年度上期 第三種電気主任技術者試験 理論科目A問題問12
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント