概要
過渡解析の計算問題です。
RL回路と、RC回路に分かれて計算する必要があるため、計算量が多くなります。
RL回路と、RC回路の両方の過渡解析が出来ることが必要であるため、難しめな問題です。
キーワード
過渡解析
問題
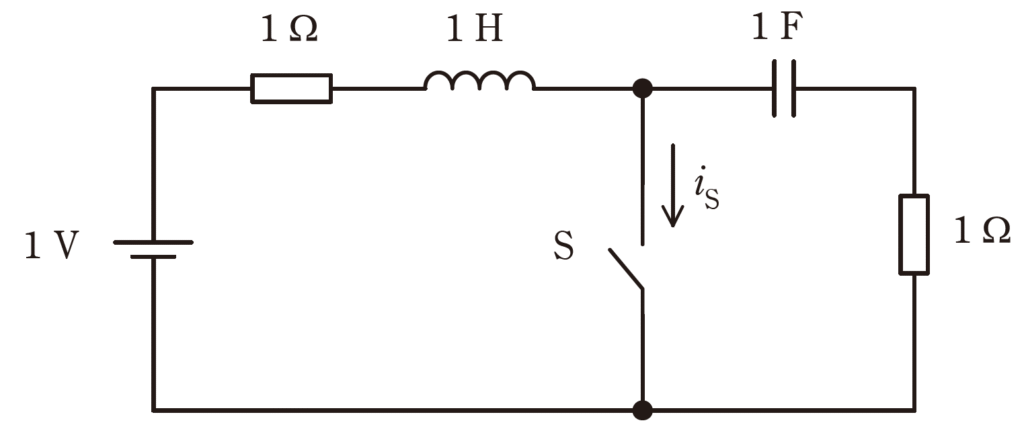
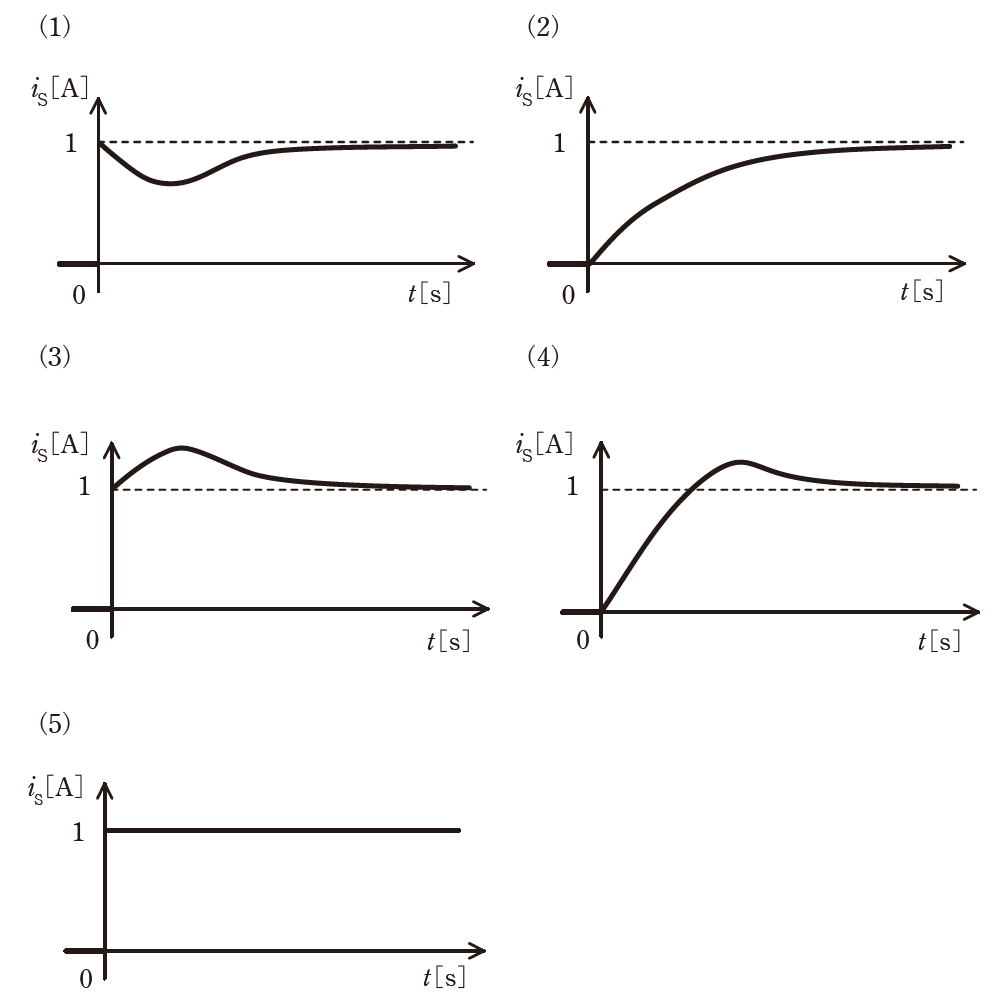
図の回路のスイッチ S を\(t=0 s\) で閉じる。電流 \(i_S [A]\)の波形として最も適切
に表すものを次の(1)~(5)のうちから一つ選べ。
ただし、スイッチS を閉じる直前に、回路は定常状態にあったとする。
答え
(5)
解説テキスト リンク
回答解説
回答の流れ
(a)スイッチ投入前
(1) スイッチSを投入前の各電圧・電流を確認する
(b)スイッチ投入後
(2) スイッチS投入後の回路を確認する
(c)スイッチSより左側のRL回路の電流\(i_1\)の過渡解析をする
(3) RL回路の微分方程式を立てる
(4) 過渡電流\(i_{ts1}\)を求める
(5) 定常電流\(i_{ss1}\)を求める
(6) 初期値から過渡解の係数\(k_1\)を求める
(7) 一般解\(i_1\)を求める
(d)スイッチSより右側のRC回路の過渡解析をする
(8) RC回路の微分方程式を立てる
(9) 過渡電圧\(v_{ct}\)を求める
(10) 定常電圧\(v_{cs}\)を求める
(11) 初期値から過渡解の係数\(k_2\)を求める
(12) 一般解\(v_c\)を求める
(13) RC回路の電流\(i_2\)を求める
(e)スイッチSを流れる電流\(i_S\)を計算する
(a)スイッチ投入前
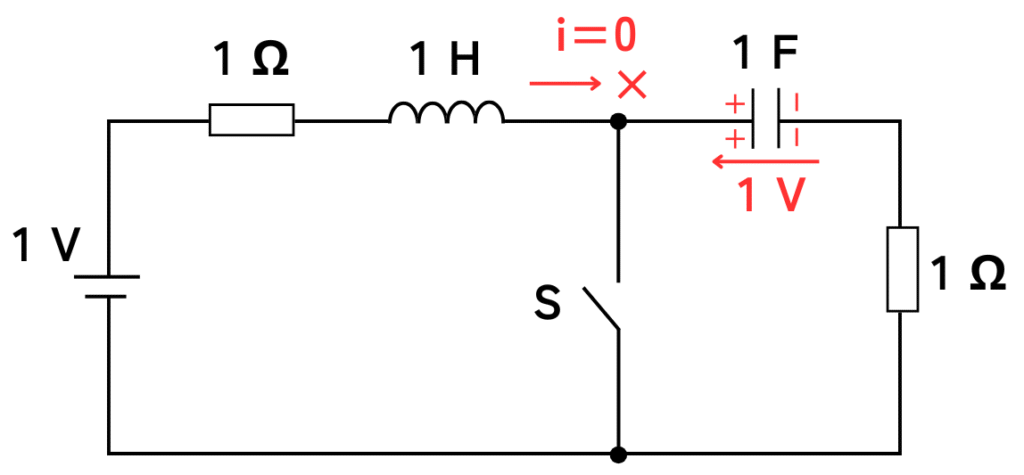
(1)スイッチSを投入前の各電圧・電流を確認する
スイッチSが開放状態で定常状態の時、コンデンサに電荷が充電されて電圧\(V_C=1V\)となります。
この時、回路にはこれ以上電流が流れなくなります。
(b)スイッチ投入後
(2)スイッチS投入後の回路を確認する
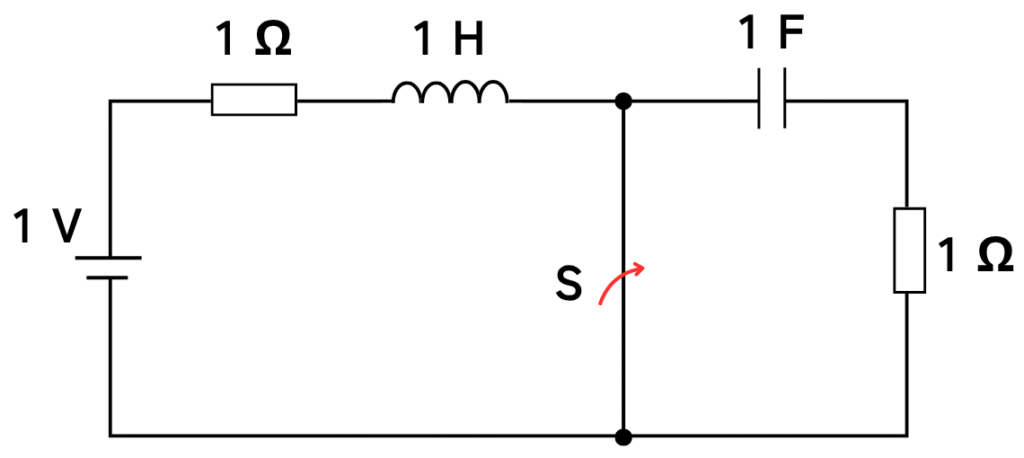
➡
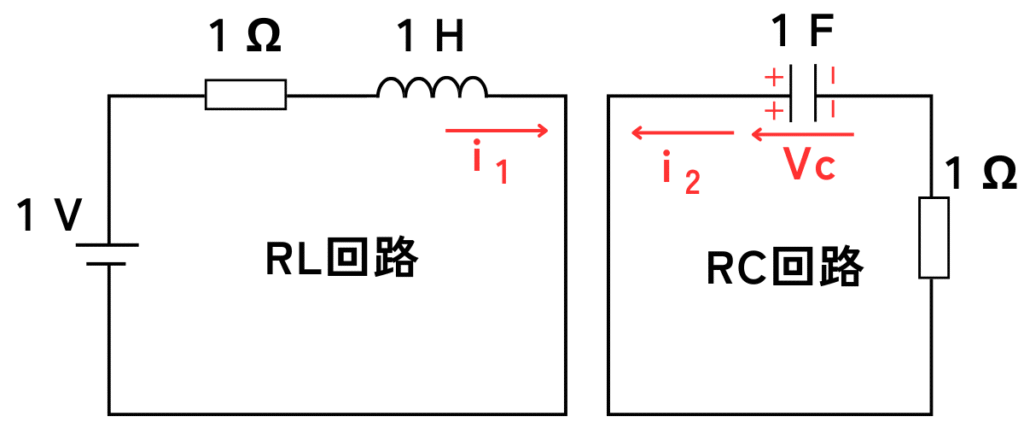
スイッチSを投入すると2つの閉回路ができます。
スイッチSより左側のRL回路と、右側のRC回路の二つの回路に分けて考えていきます。
(c)スイッチSより左側のRL回路の電流\(i_1\)の過渡解析をする
(3)RL回路の微分方程式を立てる
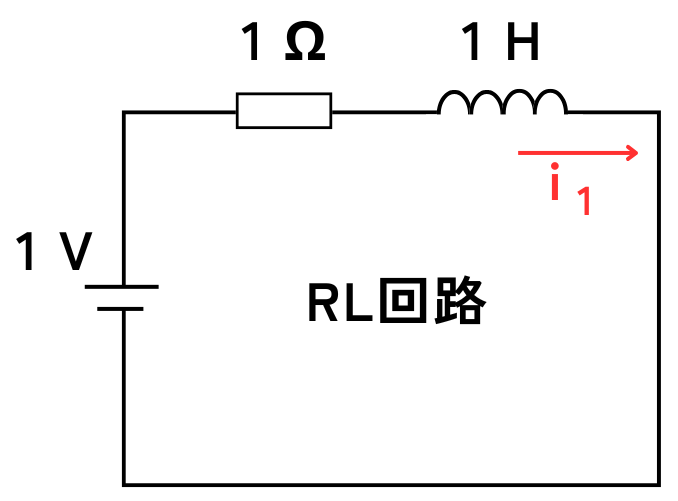
キルヒホッフの電圧則から、RL回路の方程式を立てると次式となります。
\(E=i_1R+L\frac{di_1}{dt}\)
\(E=1V\)、\(R=1Ω\)、\(L=1H\)なので、
\(1=i_1+\frac{di_1}{dt}\) …①
になります。
(4)過渡電流\(i_{ts1}\)を求める
過渡電流を\(i_{ts1}=k_1e^{-s_1t}\)
とします。\(i_{ts1}\)を時間微分すると、
\(\frac{di_{ts1}}{dt}=-s_1k_1e^{-s_1t}\)
①式から、過渡回路の方程式を立てると、
\(0=k_1e^{-s_1t}-s_1k_1e^{-s_1t}=(1-s_1)k_1e^{-s_1t}\)
⇔\(s_1=1\)
よって、過渡電流は\(i_{ts1}=k_1e^{-t}\) …②
となります。
(5) 定常電流\(i_{ss1}\)を求める
定常状態では、電流は変化しません。
したがって、\(\frac{di_{ss1}}{dt}=0\)です。
これを①式に代入します。
\(1=i_{ss1}+\frac{di_{ss1}}{dt}=i_{ss1}\)
よって、\(i_{ss1}=1\)となりました。
(6) 初期値から過渡解の係数\(k_1\)を求める
\(t=0\)のスイッチSを投入する直前の電流は\(i=0\)でした。
したがって、スイッチSを投入直後のRL回路に流れる電流は\(i_1(0)=0\)です。
\(i_1(0)=i_{ts1}+i_{ss1}=k_1e^0+1=0\)
⇔ \(k_1=-1\)
よって、過渡電流は、\(i_{ts1}=-e^{-t}\)と求まりました。
(7) 一般解\(i_1\)を求める
\(i_1=i_{ts1}+i_{ss1}=1-e^{-t}\) …③
(d)スイッチSより右側のRC回路の過渡解析をする
(8) RC回路の微分方程式を立てる
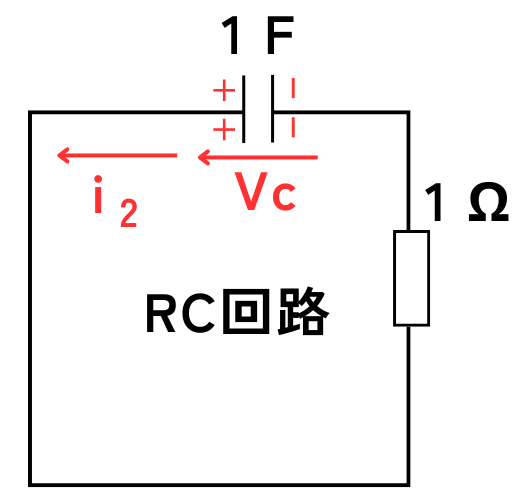
スイッチSを投入した後のRC回路は、コンデンサに蓄えられた電荷\(q\)が無くなるまで放電し続けます。
コンデンサの電圧を\(v_c\)とします。
コンデンサからRC回路中に流れる電流を\(i_2\)とします。
電流の定義式から、
\(i_2=\frac{dq}{dt}\) …④
コンデンサの電荷・静電容量・電位の関係式
\(q=Cv_c\) …⑤
④式に⑤式を代入すると、
\(i_2=C\frac{dv_c}{dt}\) …⑥
RC回路の微分方程式を立て、\(R=1Ω\)、\(C=1F\)を代入します。
\(v_c+i_2R=0\)
⇔ \(v_c+CR\frac{dv_c}{dt}=0\)
⇔ \(v_c+\frac{dv_c}{dt}=0\) …⑦
(9) 過渡電圧\(v_{ct}\)を求める
過渡電圧を\(v_{ct}=k_2e^{-s_2t}\)
とします。\(v_{ct}\)を時間微分すると、
\(\frac{dv_{ct}}{dt}=-s_2k_2e^{-s_2t}\)
⑤式から、過渡回路の方程式を立てると、
\(0=k_2e^{-s_2t}-s_2k_2e^{-s_2t}=(1-s_2)k_1e^{-s_1t}\)
⇔ \(s_2=1\)
よって、過渡電圧は\(v_{ct}=k_2e^{-t}\) …⑧
となります。
(10) 定常電圧\(v_{cs}\)を求める
定常状態では、電位は変化しません。
したがって、\(\frac{dv_{cs}}{dt}=0\)です。
これを⑦式に代入すると、定常電圧が求まります。
\(v_{cs}=0\) …⑨
(11) 初期値から過渡解の係数\(k_2\)を求める
\(t=0\)のスイッチSを投入する直前のコンデンサの電圧は\(v_c=1V\)でした。
したがって、スイッチSを投入直後のコンデンサ電圧は\(v_c(0)=1\)です。
\(v_c(0)=v_{ct}+v_{cs}=k_2e^0+0=1\)
⇔ \(k_2=1\)
よって、過渡電圧は、\(v_{ct}=-e^{-t}\) …⑩
と求まりました。
(12) 一般解\(v_c\)を求める
⑧式・⑨式より、
\(v_c=v_{ct}+v_{cs}=-e^{-t}\) …⑪
(13) RC回路の電流\(i_2\)を求める
⑤式に⑩式を代入すると
\(i_2=\frac{d}{dt}(-e^{-t})=e^{-t}\) …⑫
(e)スイッチSを流れる電流\(i_S\)を計算する

\(i_S\)は、\(i_1\)と\(i_2\)が同じ方向に合わさった電流なので、③式と、⑫式を代入すると、
\(i_S=i_1+i_2=(1-e^{-t})+e^{-t}=1\)
以上より、(5)1 が答えとなります。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和4年度下期 第三種電気主任技術者試験 理論科目A問題問10
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント