概要
RLC直列・並列回路の問題です。
コイルLとコンデンサCが共振中の各素子の電圧・電流についての理解が問われる論説問題ですが、わからない場合でも計算することで回答を導き出せます。
キーワード
交流回路、オームの法則、RLC直列回路、RLC並列回路、共振、共振条件
問題
実効値\(V[V]\)、角周波数\(ω[rad/s]\)の交流電圧源、\(R[Ω]\)の抵抗R、インダクタンス\(L[H]\)のコイルL、静電容量\(C[F]\)のコンデンサCからなる共振回路に関する記述として、正しいものと誤りのものの組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
(a)RLC直列回路の共振状態において、LとCの端子間電圧の大きさはともに0である。
(b)RLC並列回路の共振状態において、LとCに電流は流れない。
(c)RLC直列回路の共振状態において交流電圧源を流れる電流は、RLC並列回路の共振状態において交流電圧源を流れる電流と等しい。
| (a) | (b) | (c) | |
| (1) | 誤り | 誤り | 正しい |
| (2) | 誤り | 正しい | 誤り |
| (3) | 正しい | 誤り | 誤り |
| (4) | 誤り | 誤り | 誤り |
| (5) | 正しい | 正しい | 正しい |
答え
(1)
解説テキスト リンク
回答解説
解答の流れ
(a) RLC直列回路の計算
(1) 共振状態の電流を計算する
(2) Lの端子間電圧\(V_L\)を計算する
(3) Cの端子間電圧\(V_C\)を計算する
(4) まとめ ⇒ (a)の解答
(b) RLC並列回路の計算
(5) 共振状態の電流を計算する
(6) Lに流れる電流\(I_L\)を計算する
(7) Cに流れる電流\(I_C\)を計算する
(8) まとめ ⇒ (b)の解答
(c) (1)・(5)を比較する ⇒ (c)の解答
(a) RLC直列回路の計算
(1) 共振状態の電流を計算する
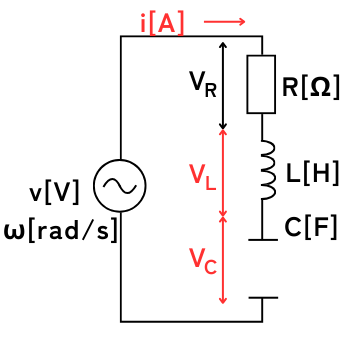
RLC直列回路のインピーダンス\(\dot{Z}\)は、
\(\dot{Z}=R+jωL+\frac{1}{jωC}\)
⇔\(\dot{Z}=R+j(ωL-\frac{1}{ωC})\) …①
共振状態という条件は、式中の虚数項(\(j\)の項)が0になることを表すので、①式中の共振条件は、次式となります。
\(ωL-\frac{1}{ωC}=0\) …②
②式を①式に代入すると、
\(\dot{Z}=R\) …③
オームの法則から電流を求めると、
\(\displaystyle i=\frac{v}{\dot{Z}}=\frac{v}{R}\)
(2) Lの端子間電圧\(V_L\)を計算する
Lの端子間電圧\(V_L\)は、コイルのリアクタンスが\(jωL\)なので、
\(\displaystyle V_L=jωLi=jωL\frac{v}{R}\)
(3) Cの端子間電圧\(V_C\)を計算する
Cの端子間電圧\(V_C\)は、コンデンサのリアクタンスが\(\frac{1}{jωC}=-j\frac{1}{ωC}\)なので、
\(\displaystyle V_C=-j\frac{i}{ωC}=-j\frac{v}{ωCR}\)
(4) まとめ ⇒ (a)の解答
Lの端子間電圧\(V_L\)は、\(\displaystyle V_L=jωL\frac{v}{R}\)
Cの端子間電圧\(V_C\)は、\(\displaystyle V_C=-j\frac{v}{ωCR}\)
であることから、LとCの端子間電圧の大きさはともに0ではありません。 ⇒ (a)は誤り
(b) RLC並列回路の計算
(5) 共振状態の電流を計算する
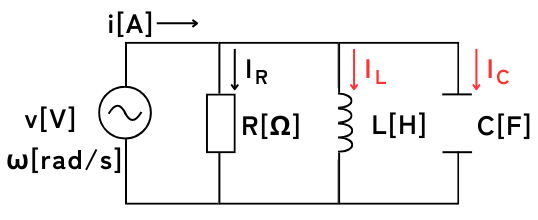
RLC並列回路のインピーダンス\(\dot{Z}\)は、
\(\displaystyle \frac{1}{\dot{Z}}=\frac{1}{R}+\frac{1}{jωL}+\frac{1}{\frac{1}{jωC}}\)
⇔\(\displaystyle \frac{1}{\dot{Z}}=\frac{1}{R}-j\frac{1}{ωL}+jωC\)
⇔\(\displaystyle \frac{1}{\dot{Z}}=\frac{1}{R}+j(ωC-\frac{1}{ωL})\) …①
共振状態という条件は、式中の虚数項(\(j\)の項)が0になることを表すので、①式中の共振条件は、次式となります。
\(\displaystyle ωC-\frac{1}{ωL}=0\) …②
②式を①式に代入すると、
\(\displaystyle \frac{1}{\dot{Z}}=\frac{1}{R}\)
⇔ \(\dot{Z}=R\) …③
オームの法則から電流を求めると、
\(\displaystyle i=\frac{v}{\dot{Z}}=\frac{v}{R}\)
(6) Lに流れる電流\(I_L\)を計算する
Lの端子間電圧\(V_L\)は、電源電圧\(v\)なので、Lに流れる電流\(I_L\)は、
\(\displaystyle I_L=\frac{V_L}{jωL}=-j\frac{V_L}{ωL}\)
(7) Cに流れる電流\(I_C\)を計算する
Cの端子間電圧\(V_C\)は、電源電圧\(v\)なので、Cに流れる電流\(I_C\)は、
\(\displaystyle I_C=\frac{V_C}{\frac{1}{jωC}}=jωCv\)
(8) まとめ ⇒ (b)の解答
Lに流れる電流\(I_L\)は、\(\displaystyle I_L=-j\frac{V_L}{ωL}\)
Cに流れる電流\(I_C\)は、\(I_C=jωCv\)
であることから、LとCに電流は流れます。 ⇒ (b)は誤り
(c) (1)・(5)を比較する ⇒ (c)の解答
共振状態の電流は、(1)も(5)も、共に
\(\displaystyle i=\frac{v}{\dot{Z}}=\frac{v}{R}\)
したがって、RLC直列回路の共振状態において交流電圧源を流れる電流は、RLC並列回路の共振状態において交流電圧源を流れる電流と等しい。 ⇒ (c)は正しい
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和3年度 第三種電気主任技術者試験 理論科目A問題問9
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント