概要
発振回路の回路解析の問題です。
問17と問18の選択問題であり、問17に比べて圧倒的に完答が難しい問題であるため、あまり選択されない問題だったかと思われます。
(a)問題は、発振回路の直流バイアスの計算
オーソドックスな問題ですが、バイポーラトランジスタの解析に関する知識が一通り問われるような問題です。標準~少々難しいの難易度ですが、電子回路で必要な知識が学べるような良問です。
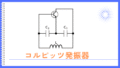
(b)問題は、コルピッツ発振器の発振条件に関する計算問題です。
コルピッツ発振器の問題は、何となく共振周波数を算出して正解できたという人は居ると思いますが、全てを理解した上で回答できた人は少ないかと思われます。
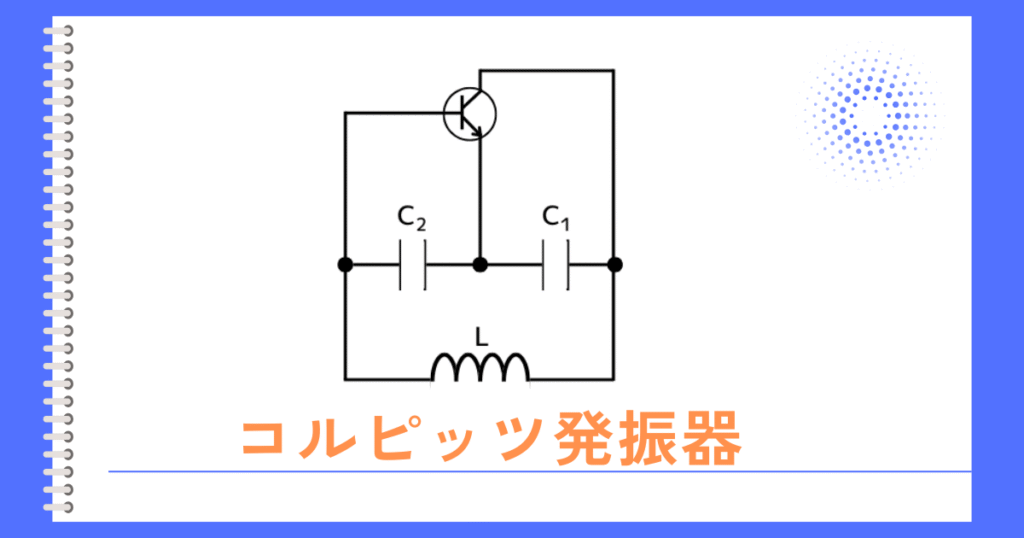
コルピッツ発振器を完全に理解するためには下記3つについて理解した上で、手順の多い計算をして、やっと発振周波数を得ることができます。
・正帰還
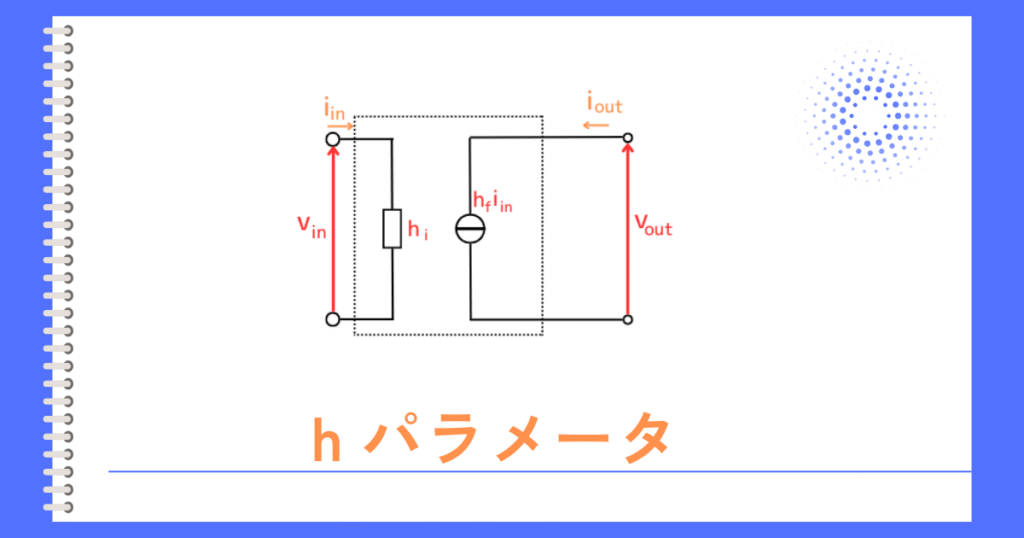
・hパラメータとhパラメータを使用した簡易小信号等価回路
・発振回路の2つの発振条件(振幅条件、周波数条件)
キーワード
エミッタ接地回路、コルピッツ発振回路
問題
発振回路について、次の(a)及び(b)の問に答えよ。
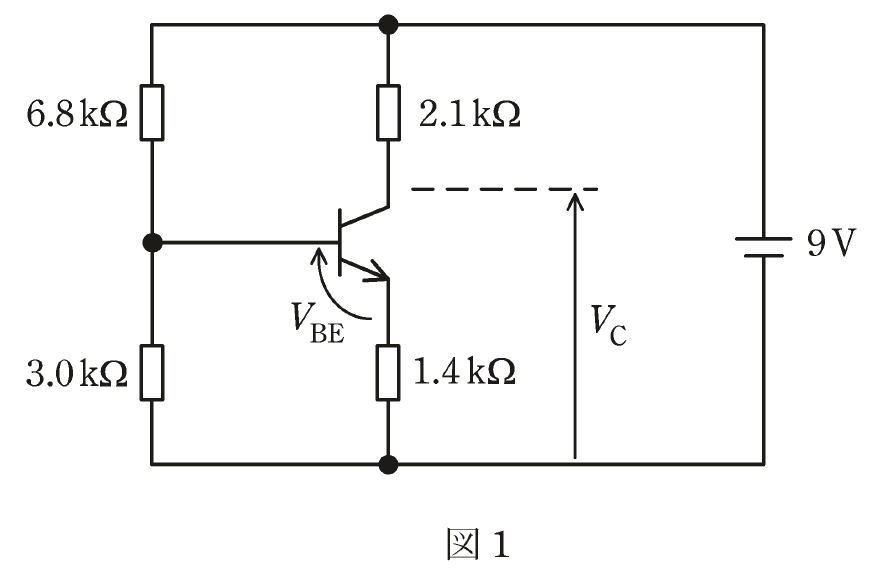
(a)図1は、ある発振回路のコンデンサを開放し、同時にコイルを短絡した、直流分を求めるための回路図である。
図中の電圧\(V_c[V]\)として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、図中の\(V_{BE}\)並びにエミッタ接地トランジスタの直流電流増幅率\(h_{FE}\)をそれぞれ\(V_{BE}=0.6V\)、\(h_{FE}=100\)とする。
(1)3 (2)4 (3)5 (4)6 (5)7
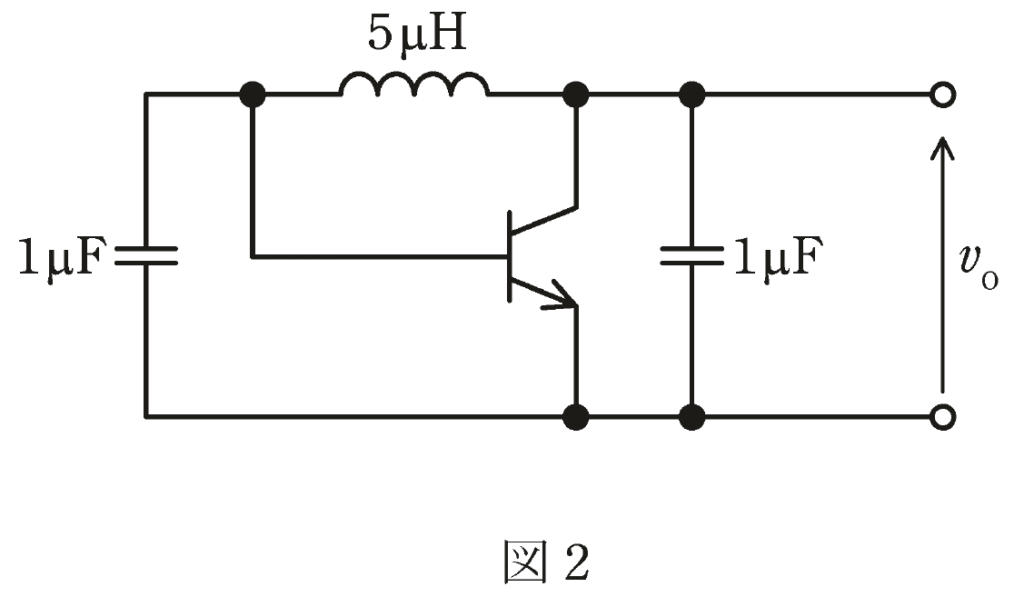
(b)図2は、ある発振回路のトランジスタに接続されている、電極間のリアクタンスを示している。
ただし、バイアス回路は省略している。
この回路が発振するとき、発振周波数\(f_0[kHz]\)はどの程度の大きさになるか、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、発振周波数は、図に示されている素子の値のみにより定まるとしてよい。
(1)0.1 (2)1 (3)10 (4)100 (5)1000
答え
(a)(4)
(b)(4)
解説テキスト リンク
回答解説
(a)の解答の流れ
①トランジスタのベース電圧\(V_B\)を求める
②エミッタ電圧\(V_E\)を求める
③エミッタ電流\(I_E\)を求める
④コレクタ電流\(I_C\)を求める
⑤コレクタ電圧\(V_C\)を求める
①トランジスタのベース電圧\(V_B\)を求める

ベース電圧\(V_B\)は、電源電圧\(V_{CC}=9V\)から6.8kΩと3.0kΩに分圧された電圧です。
\(\displaystyle \begin{eqnarray}
V_B&=&\frac{3.0}{6.8+3.0}・9 \\ \\
&=&2.755V
\end{eqnarray}\)
②エミッタ電圧\(V_E\)を求める
エミッタ電圧\(V_E\)は、ベース電圧\(V_B\)から、ベース-エミッタ間電圧\(V_{BE}\)だけ低い電圧であるため、
\(V_E=V_B-V_{BE}=2.755-0.6=2.155V\)
③エミッタ電流\(I_E\)を求める
エミッタに接続された抵抗\(R_E=1.4\)kΩに、エミッタ電圧\(V_E\)が印加されるので、オームの法則からエミッタ電流\(I_E\)が求まります。
\(\displaystyle I_E=\frac{V_E}{R_E}=\frac{2.155}{1.4×10^3}=1.539×10^{-3}=1.539[mA]\)
④コレクタ電流\(I_C\)を求める
エミッタ電流\(I_E\)は、ベース電流\(I_B\)とコレクタ電流\(I_C\)が足された電流です。
\(I_E=I_B+I_C\)
エミッタ接地トランジスタの直流電流増幅率\(h_{FE}=100\)の条件が、問題文から与えられているので、\(I_B\)と\(I_C\)の関係は次のように表されます。
\(I_C=h_{FE}I_B=100I_B\)
⇔ \(\displaystyle I_B=\frac{1}{100}I_C\)
エミッタ電流\(I_E\)の式に代入すると、
\(\displaystyle I_E=\frac{1}{100}I_C+I_C=\frac{101}{100}I_C\)
⇔ \(\displaystyle I_C=\frac{100}{101}I_E=\frac{100}{101}・1.539=1.524[mA]\)
⑤コレクタ電圧\(V_C\)を求める
コレクタ電圧\(V_C\)は、電源電圧\(V_{CC}=9V\)から、コレクタ抵抗\(R_C=2.1\)kΩで電圧降下した分の電圧です。したがって、
\(V_C=V_{CC}-I_CR_C=9-1.524×10^{-3}・2.1×10^3=9-3.2=5.8V≒6V\)
以上より、(a)問題は(4)6V が答えです。
(b)の解答の流れ
①発振条件を整理する
②回路図を解析しやすいように書き変える
③回路のアドミタンス\(Y\)の式を導出する
④回路の共振周波数\(f_0\)を求める
①発振条件を整理する
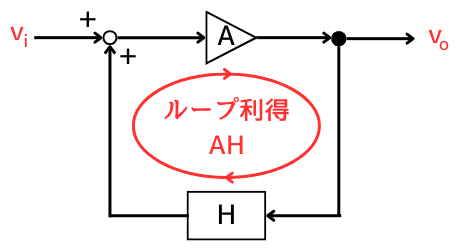
問題の回路は、正帰還されたオペアンプの回路としてみることが出来ます。
正帰還された回路が発振するには2つの条件があります。
1.振幅条件 \(AH≧1\)
2.周波数条件 \(AH\)の虚数項が0(\(AH\)の位相角が0)
本問は、発振周波数\(f_0[kHz]\)について求めたいため、周波数条件について考えます。
周波数条件は、並列接続された回路の共振周波数を求める事と同じです。
共振周波数は、並列回路の場合は、アドミタンスが\(Y=0\)となる周波数です。
したがって、出力電圧から見た回路の\(Y=0\)となる条件を求めていきます。
※周波数条件について詳細に知りたい場合は、解説テキストリンクのコルピッツ発振器を参照してください。
②回路図を解析しやすいように書き変える
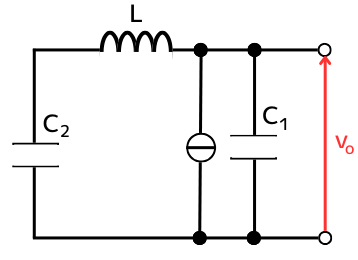
トランジスタは、ベース電流\(I_B\)を電流増幅率\(h_{FE}\)倍する電流源として考えることが出来るので、トランジスタを電流源として書き変えます。
\(v_o\)について考えるとき、重ねの理から電流源は開放として取り扱います。
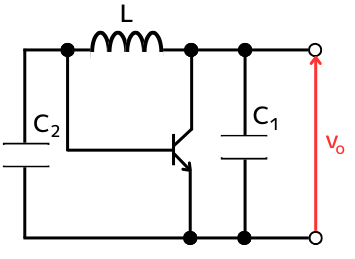
⇨
⇨
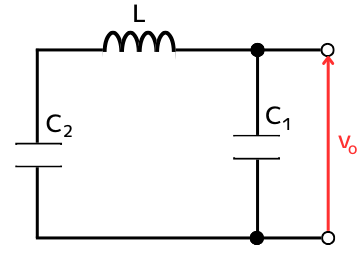
③回路のアドミタンス\(Y\)の式を導出する
回路全体のアドミタンス\(Y\)は、リアクトル\(L\)と、コンデンサ\(C_2\)の直列接続に、コンデンサ\(C_1\)を並列接続された回路なので、次式となります。
\(\displaystyle Y=jωC_1+\frac{1}{jωL+\frac{1}{jωC_2}}\)
④回路の共振周波数\(f_0\)を求める
共振周波数\(f_0\)は、\(Y=0\)となる周波数なので、
\(\displaystyle \begin{eqnarray}
Y&=&jωC_1+\frac{1}{jωL+\frac{1}{jωC_2}} =0\\ \\
&⇔ &jωC_1+\frac{jωC_2}{1-ω^2LC_2} =0\\ \\
&⇔ &C_1+\frac{C_2}{1-ω^2LC_2} =0 \\ \\
&⇔ &\frac{C_1}{C_2}+\frac{1}{1-ω^2LC_2} =0 \\ \\
&⇔ &\frac{C_1}{C_2}(1-ω^2LC_2)+1 =0 \\ \\
&⇔ &C_1(1-ω^2LC_2)+C_2 =0 \\ \\
&⇔ &ω^2LC_1C_2=C_1+C_2 \\ \\
&⇔ &ω=\sqrt{\frac{C_1+C_2}{LC_1C_2}} \\ \\
&⇔ &2πf=\sqrt{\frac{C_1+C_2}{LC_1C_2}} \\ \\
&⇔ &f=\frac{1}{2π}\sqrt{\frac{C_1+C_2}{LC_1C_2}} \\
\end{eqnarray}\)
\(C_1=C_2=1μF\)、\(L=5μH\)を代入すると、
\(\displaystyle f_0=\frac{1}{2π}\sqrt{\frac{2×10^{-6}}{5×10^{-6}×1×10^{-6}×1×10^{-6}}} =100709Hz\)
以上より、(b)問題は(4)100[kHz] が答えです。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和3年度 第三種電気主任技術者試験 理論科目B問題問18
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント