【電験三種：理論】令和３年度　問１４

概要

ブリッジ回路の誤差率を求める問題です。
ブリッジ回路の平衡条件を理解が問われる問題です。

キーワード
ブリッジ回路、誤差率

　

問題

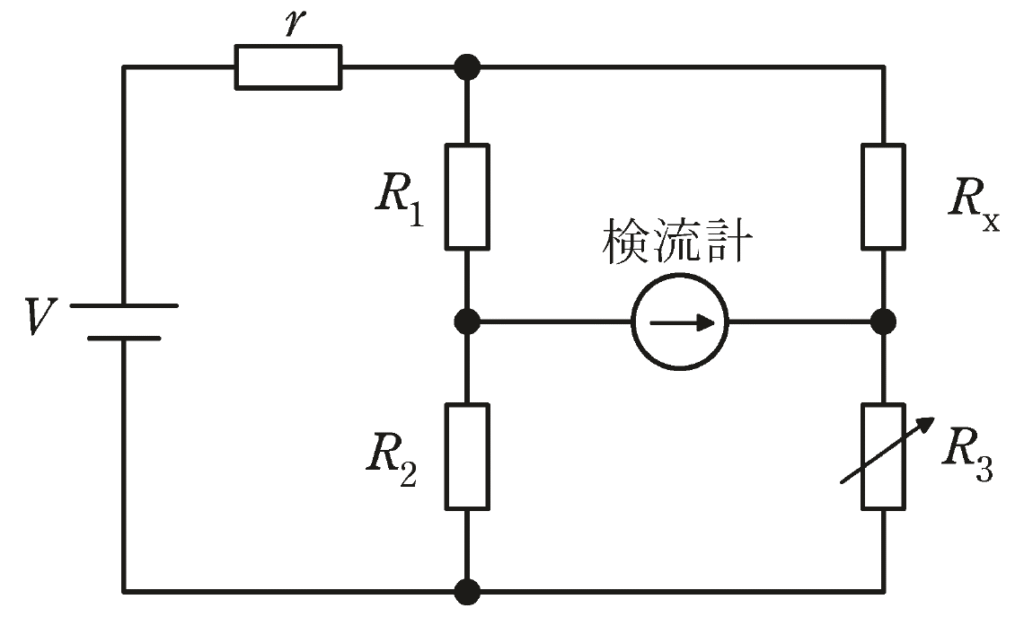
図のブリッジ回路を用いて、未知の抵抗の\(R_x[Ω]\)を推定したい。
可変抵抗\(R_3\)を調整して、検流計に電流が流れない状態を探し、平衡条件を満足する\(R_x[Ω]\)の値を求める。
求めた値が真値と異なる原因が、\(R_k（k=1,2,3）\)の真値からの誤差\(ΔR_k\)のみである場合を考え、それらの誤差率\(ε_k=\frac{ΔR_k}{R_k}\)が次の値であったとき、\(R_x\)の誤差率として、最も近いものを次の（１）～（５）のうちから一つ選べ。
\(ε_1=0.01\)、\(ε_2=-0.01\)、\(ε_3=0.02\)

（１）0.0001　　　（２）0.01　　　（３）0.02　　　（４）0.03　　　（５）0.04

　

答え

(５)

解説テキスト　リンク

　

回答解説

解答の流れ
①\(R_x[Ω]\)の真値をブリッジの平衡条件から求める
②\(R_1\)、\(R_2\)、\(R_3\)の誤差\(ΔR_1\)、\(ΔR_2\)、\(ΔR_3\)を求める
③\(R_x\)の測定値\(R_x+ΔR_x\)を求める
④誤差\(ΔR_x\)を求める
⑤誤差率\(ε_x\)を求める

①\(R_x[Ω]\)の真値をブリッジの平衡条件から求める

ブリッジの平衡条件から、
\(R_2R_x=R_1R_3\)

⇔\(\displaystyle R_x=\frac{R_1R_3}{R_2}\)

　

---

②\(R_1\)、\(R_2\)、\(R_3\)の誤差\(ΔR_1\)、\(ΔR_2\)、\(ΔR_3\)を求める

誤差率\(ε\)、誤差\(ΔR\)、真値\(R\)の関係式は、
\(\displaystyle ε=\frac{ΔR}{R}\)　⇔　\(ΔR=εR\)
となり、誤差を求める式が得られます。

問題文から、誤差率は、それぞれ\(ε_1=0.01\)、\(ε_2=-0.01\)、\(ε_3=0.02\)なので、
\(ΔR_1=ε_1R_1=0.01R_1\)
\(ΔR_2=ε_2R_2=-0.01R_2\)
\(ΔR_3=ε_3R_3=0.02R_3\)

---

③\(R_x\)の測定値\(R_x+ΔR_x\)を求める

誤差\(ΔR_x\)の定義が真値\(R_x\)と測定値\(M\)の差であることから、式変形すると測定値が得られます。
\(ΔR_x=R_x-M\)　⇔　\(M=R_x+ΔR_x\)

\(\begin{eqnarray}
M&=&R_x+ΔR_x \\ \\
&=&\frac{(R_1+ΔR_1)(R_3+ΔR_3)}{R_2+ΔR_2} \\ \\
&=&\frac{1.01R_1・1.02R_3}{0.99R_2}\\ \\
&=&1.04\frac{R_1・R_3}{R_2}\\ \\
&=&1.04R_x
\end{eqnarray}\)

　

---

④誤差\(ΔR_x\)を求める

③の項目で求めた測定値の計算結果から、式変形すると誤差\(ΔR_x\)が求まります。
\(R_x+ΔR_x=1.04R_x\)
⇔　\(ΔR_x=0.04R_x\)

　

---

⑤誤差率\(ε_x\)を求める

誤差率\(ε\)の式\( ε=\frac{ΔR}{R}\)から、

\(\displaystyle ε_x=\frac{ΔR_x}{R_x}=\frac{0.04R_x}{R_x}=0.04\)

以上より、（５）0.04　が答えとなります。

　

　

出典元

一般財団法人電気技術者試験センター　（https://www.shiken.or.jp/index.html）
令和３年度　第三種電気主任技術者試験　理論科目Ａ問題問１４

参考書