概要
一様な磁界中に電流を流した時の電磁力と、電磁力によって生じるモーメントを求める問題です。
どちらも基礎レベルではありますが、電磁力に関する知識と、力学的な知識が要求されます。
キーワード
電磁力、偶力、モーメント
問題
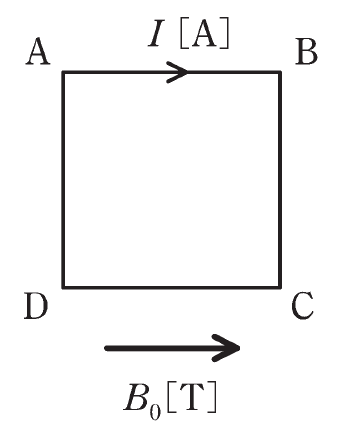
平等な磁束密度\(B_0[T]\)のもとで、一辺の長さが\(h[m]\)の正方形ループABCDに直流電流\(I[A]\)が流れている。
\(B_0\)の向きは辺ABと平行である。
\(B_0\)がループに及ぼす電磁力として、正しいものを次の(1)~(5)のうちから一つ選べ。
(1)大きさ\(2IhB_0[N]\)の力
(2)大きさ\(4IhB_0[N]\)の力
(3)大きさ\(Ih^2B_0[N・m]\)の偶力のモーメント
(4)大きさ\(2Ih^2B_0[N・m]\)の偶力のモーメント
(5)力も偶力のモーメントも働かない
答え
(3)
要点整理
電磁力について
電磁力は、電流と磁界の相互作用によって発生した力です。電磁力の式を端的に示すと下式となります。
\(F=IBlsinθ\)
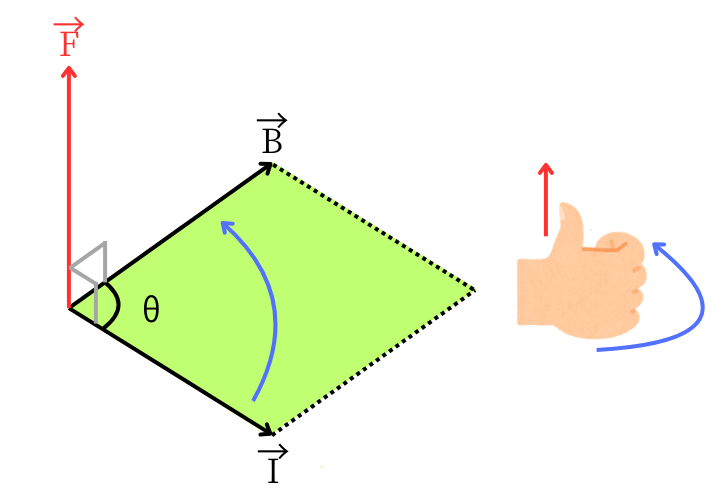
電磁力の式について解説します。
電磁力\(\vec{F}[N]\)は、電流\(\vec{I}[A]\)と、磁束密度\(\vec{B}[T]\)の外積で表されます。これを式で表すと、
\(\vec{F}=\vec{I}\times\vec{B}\)
となります。ベクトルの式に出てくる \(×\) の記号は、外積を表します。
電磁力の向きは、電流の向きから磁界の向きに右ねじの法則で回したときに、親指が向く向きです。
\(\vec{F}\)の大きさは、\(\vec{I}\)と\(\vec{B}\)の作る平行四辺形の面積と同じです。つまり、
\(|F|=|I| |B| sinθ\)
です。導体の長さを\(l[m]\)とすると
\(F=IBlsinθ\)
と求まります。
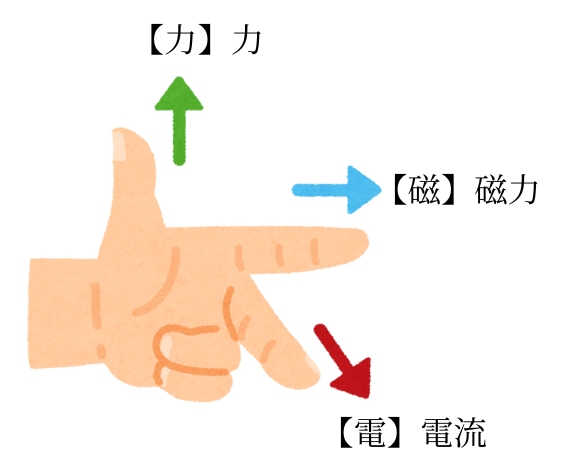
上記で示した電流・磁界・力の向きを簡単に表現すると、フレミング左手の法則で示されます。
偶力について
偶力とは、次の3条件が揃った力です。
①大きさが等しい
②向きが正反対
③平行(同じ直線上にない)2つの力
偶力は、合力をもとめられないので1対の力として扱います。
偶力が1つの物体に働くと、物体は回転します。
偶力と、偶力ではない力の例を図に示します。

偶力となる2つの力の例です
①大きさが等しく
②向きが正反対で
③平行(同じ直線上にない)



偶力でない力の例です
①大きさが等しくない
②向きが正反対でない
③平行でない
偶力を使った物の例
ネジは、ドライバーを使って回転させるとき、手で偶力を発生させて回しています。
モーメントについて
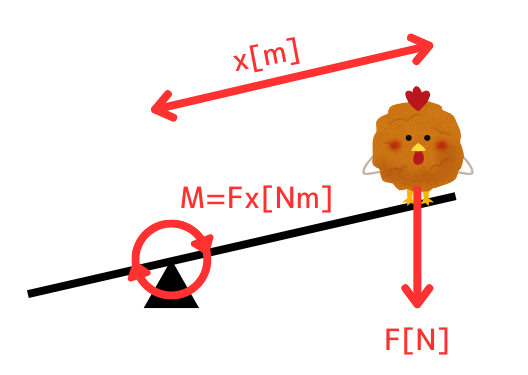
モーメントとは、支点にかかる物体を回転させる力のことです。
モーメント\(M[Nm]\)は、かかる力\(F[N]\)と、支点からの距離\(x[m]\)の積で表します。
\(M=Fx[Nm]\)
回答解説
まずは、磁界\(B_0[T]\)中に流れる電流\(I[A]\)によって生じる電磁力について求めます。
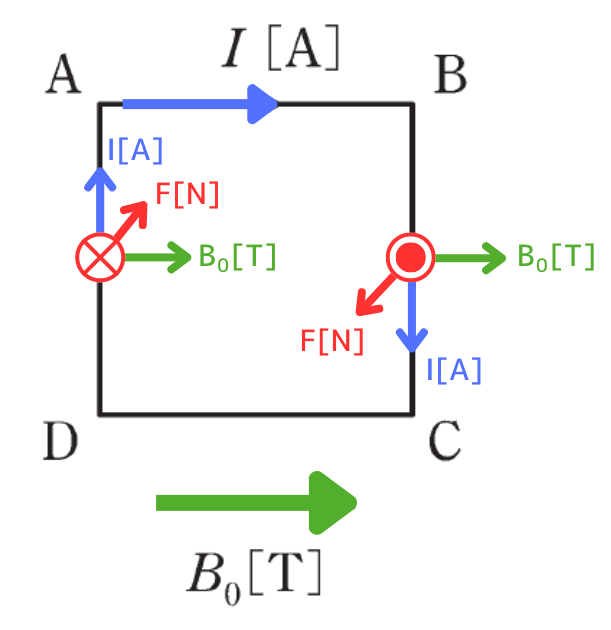
発生する電磁力は、
B→C間に流れる電流によって、
画面奥から手前方向に
\(F=IB_0h[N]\) …①
の力が発生します。
D→A間に流れる電流によって、
画面手前から奥方向に
\(F=IB_0h[N]\) …①
の力が発生します。
次に、発生した電磁力による偶力のモーメントを求めます。
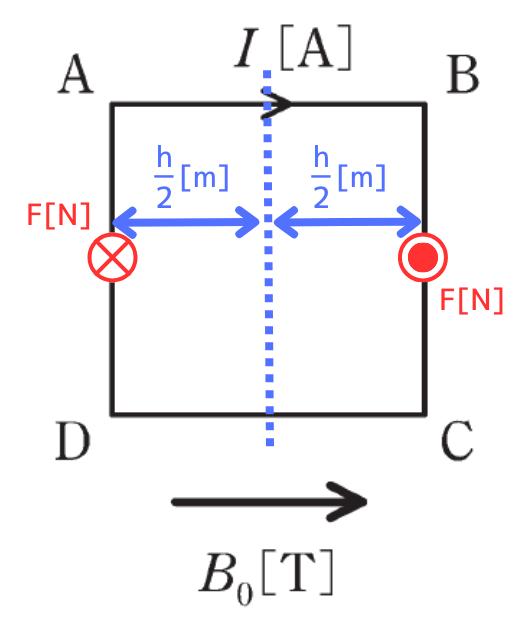
AB間、DC間の中心の位置が、回転する中心となります。
したがって、モーメントにかかる距離は、
\(x=\frac{h}{2}\) …②
です。
①・②式より、
\(\displaystyle M=2Fx=2IB_0h・\frac{h}{2}\)
⇒\(M=Ih^2B_0[N・m]\)
以上より、答えは (3)大きさ\(Ih^2B_0[N・m]\)の偶力のモーメントです。
出典元
令和2年度第三種電気主任技術者試験 理論科目A問題問3
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント