概要
環状ソレノイドの磁気回路の問題です。
磁気回路は割と出題されやすいことと、電気回路と同じように解答出来る事から、確実に解けるようになりたい問題です。
キーワード
磁気回路、磁気抵抗、透磁率
問題
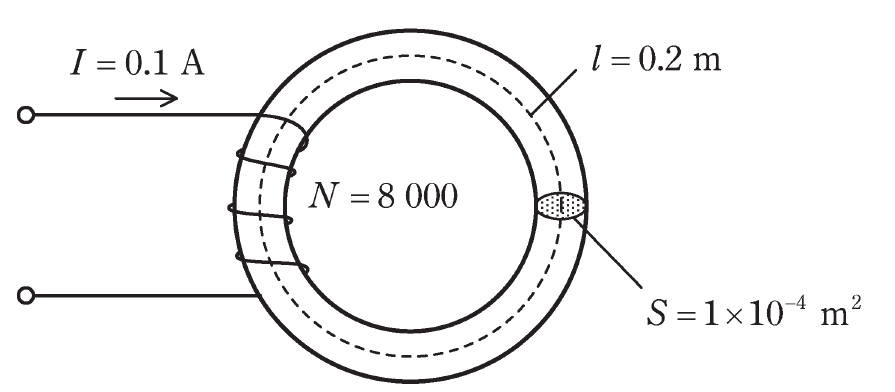
図のように、磁路の長さ\(l=0.2m\)、断面積\(S=1×10^{-4}m^2\)の環状鉄心に巻数\(N=8000\)の銅線を巻いたコイルがある。
このコイルに直流電流\(I=0.1A\)を流したとき、鉄心中の磁束密度は\(B=1.28T\)であった。
このときの鉄心の透磁率\(μ\)の値\([H/m]\)として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、コイルによって作られる磁束は、鉄心中を一様に通り、鉄心の外部に漏れないものとする。
(1)\(1.6×10^{-4}\) (2)\(2.0×10^{-4}\) (3)\(2.4×10^{-4}\)
(4)\(2.8×10^{-4}\) (5)\(3.2×10^{-4}\)
答え
(5)
要点整理
磁気回路と電気回路
磁気回路の式をまとめます。
起磁力:\(F=NI=Hl[A]\)
磁束:\(\Phi =BS[Wb]\)
磁気抵抗:\(\displaystyle R_m=\frac{l}{μS}[H^{-1}]\)
磁気回路のオームの法則
\(F=\Phi R_m\)
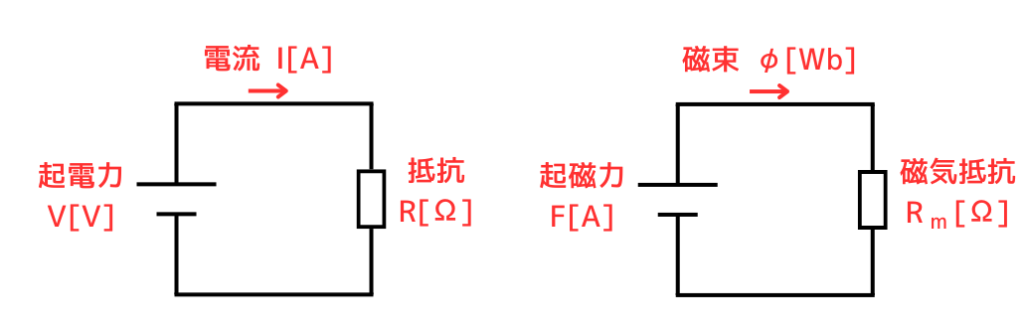
磁気回路にも、電気回路のようにオームの法則とキルヒホッフの法則がなりたちます。
| 電気回路 - 磁気回路対応表 | |
|---|---|
| 電気回路 | 磁気回路 |
| 起電力\(V[V]\) | 起磁力\(F[A]\) |
| 電流\(I[A]\) | 磁束\(\Phi [Wb]\) |
| 抵抗\(R[Ω]\) (レジスタンス) | 磁気抵抗\(R_m[H^{-1}]\) (リラクタンス) |
| オームの法則 \(V=IR\) | オームの法則 \(F=\Phi R_m\) |
起磁力の関係式
\(N\)回巻のコイルに流れる電流\(I[A]\)が起磁力を生み出すので、起磁力\(F[A]\)は、
\(F=NI[A]\) ………①
です。
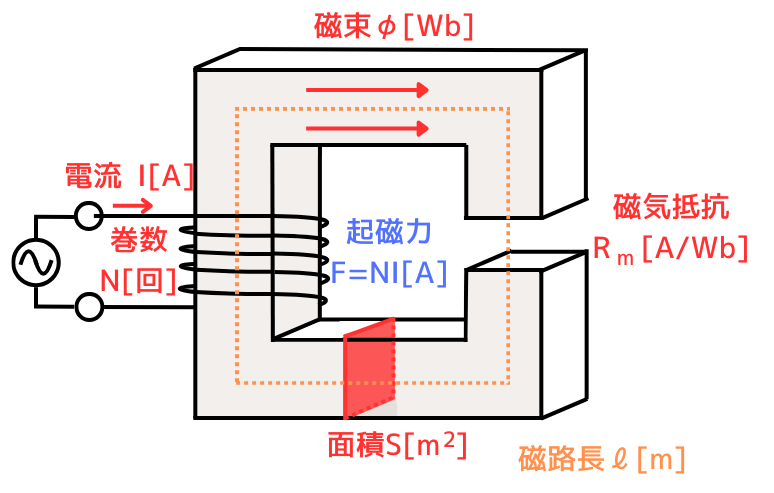
磁気回路の起磁力を生み出すコイル部分は、無限長ソレノイドとして扱います。
そのため、磁界の強さ\(H[A/m]\)、磁気回路の長さ(磁路長)\(l[m]\)としたとき、
\(F=Hl\) ………②
です。①・②式から
\(NI=Hl\)
⇔\(\displaystyle H=\frac{NI}{l}\) ………③
磁束の関係式
磁束密度\(B[T]\)は、磁束\(\Phi [Wb]\)の密度なので、磁路の面積\(S[m^2]\)を使って表すと、
\(\Phi =BS[Wb]\) ………④
⇔\(\displaystyle B=\frac{\Phi }{S}\) ………⑤
です。
磁束密度\(B[T]\)と、磁界強度\(H[A/m]\)、透磁率\(μ[H/m]\)の関係式は、
\(B=μH\) ………⑥
磁気抵抗の関係式の導出
①・③・⑥式から、
\(\displaystyle B=\frac{μNI}{l}=\frac{μF}{l}\)
となるので、⑤式を代入すると、
\(\displaystyle \frac{\Phi }{S}=\frac{μF}{l}\)
⇔\(\displaystyle \frac{F}{\Phi }=\frac{l}{μS}\) …⑥
磁気回路のオームの法則の式は次式です。
\(\displaystyle R_m=\frac{F}{\Phi }\) …⑦
⑥・⑦式を比較すると、
\(\displaystyle R_m=\frac{l}{μS}\)
となります。
以上より、\(\displaystyle R_m=\frac{l}{μS}\) が導出できました。
磁気抵抗(\(\displaystyle R_m=\frac{l}{μS}\))の式の感覚的な覚え方
①磁気回路の面積\(S\)が広くなれば、磁束\(\Phi \)が通る道は広くなります。
⇒磁束が流れやすくなり、磁気抵抗\(R_m\)は小さくなる。
②磁路長\(l[m]\)が長くなると、磁束が流れる抵抗が長くなります。
⇒磁気抵抗\(R_m\)は長くなった分、大きくなります。
③透磁率\(μ\)は、磁束がどれくらい通しやすいかを表します。
透磁率\(μ\)が大きくなると、磁束が通りやすくなります。
⇒磁気抵抗\(R_m\)は小さくなります。
回答解説
問題の環状鉄心とコイルを磁気回路に書き換えます。
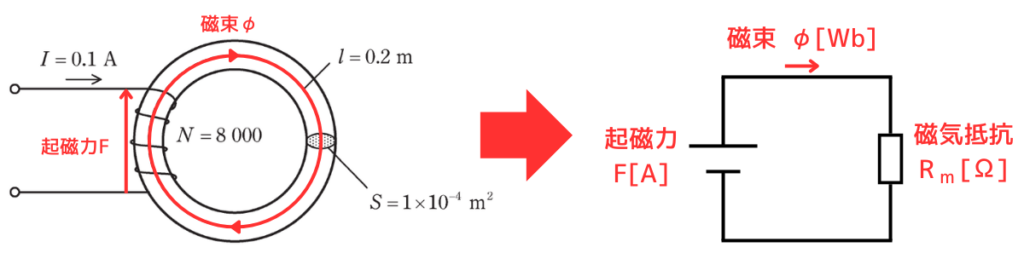
コイルの巻数と、コイルに流れる電流から発生する起磁力\(F[A]\)は、①式として表されます。
\(F=NI\) …①
磁気回路のオームの法則は、②式として表されます。
\(F=R_m \Phi\) …②
①式=②式なので、
\(NI=R_m \Phi\) …③
磁束\(\Phi[Wb]\)は、磁束密度\(B[T]\)と、鉄心の面積\(S[m^2]\)を使い、④式として表されます。
\(\Phi = BS\) …④
磁気抵抗\(R_m[H^{-1}]\)は、平均磁路長\(l[m]\)、鉄心の断面積\(S[m^2]\)、透磁率\(μ[H/m]\)を使って、⑤式として表されます。
\(\displaystyle R_m=\frac{l}{μS}\) …⑤
④・⑤式を③式に代入して\(μ\)について整理します。
\(\displaystyle NI=\frac{l}{μS}BS\)
⇔\(\displaystyle μ=\frac{lB}{NI}=\frac{0.2・1.28}{8000・0.1}=3.2×10^{-4}\)
以上より、(5) \(3.2×10^{-4}\)が答えです。
出典元
令和元年度第三種電気主任技術者試験 理論科目A問題問4
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント