概要
二重積分形AD変換器の問題です。
二重積分形AD変換器の動作原理について、問題文で事細かに説明されているため長文です。
このことから、試験中に手を出しづらい問題だと思われますが、冷静に文章を読んで考えることができれば解答できる問題です。
問題の題材である二重積分形AD変換器は、直流測定に優れていることから、デジタルマルチメータに使用されることもある回路です。
キーワード
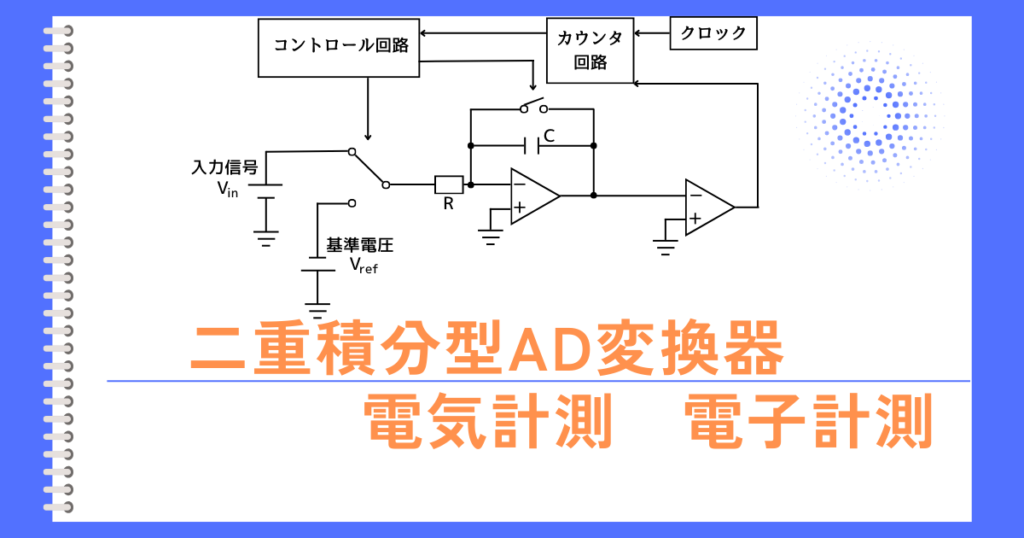
二重積分形AD変換器
問題
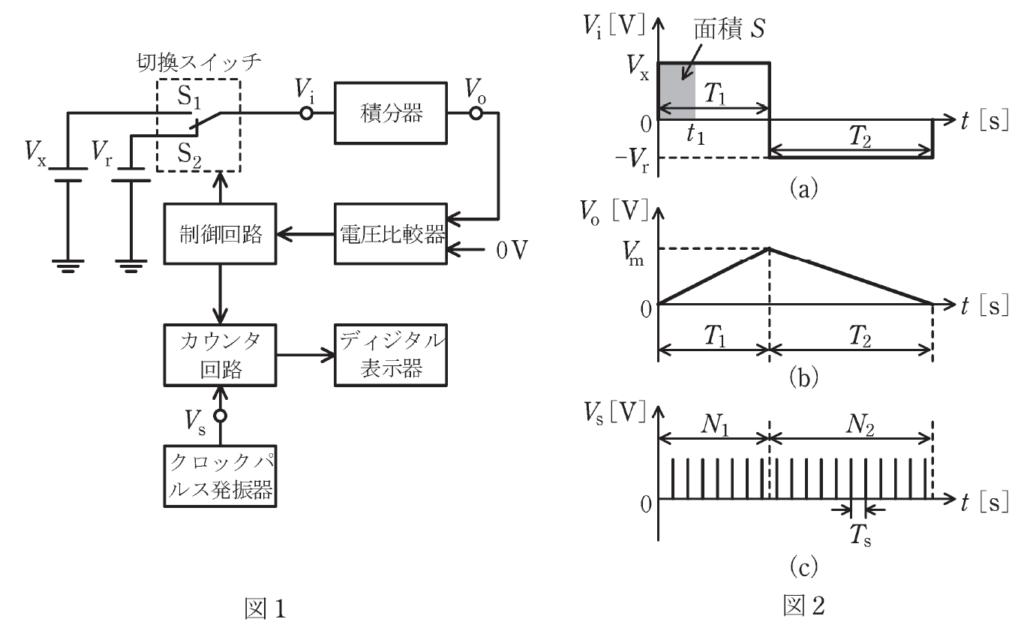
図1は、二重積分形A-D変換器を用いたディジタル直流電圧計の原理図である。
次の(a)及び(b)の問に答えよ。
(a)図1のように、負の基準電圧 \(-V_r(V_r>0)[V]\) と切換スイッチが接続された回路があり、
その回路を用いて正の未知電圧 \(V_x(>0)[V]\) を測定する。
まず、制御回路によってスイッチが \(S_1\) 側へ切り換わると、時刻 \(t=0s\) で測定電圧 \(V_x[V]\) が積分器へ入力される。
その入力電圧 \(V_i[V]\) の時間変化が図2(a)であり、積分器からの出力電圧 \(V_o[V]\) の時間変化が図2(b)である。ただし、 \(t=0s\) での出力電圧を \(V_o=0V\) とする。
時刻 \(t_1\) における \(V_o[V]\) は、入力電圧 \(V_i[V]\) の期間 \(0~t_1[s]\) で囲われる面積Sに比例する。積分器の特性で決まる比例定数を \(k(>0)\) とすると、時刻 \(t=T_1[s]\) のときの出力電圧は、 \(V_m=\fbox{(ア)}[V]\) となる。
定められた時刻 \(t=T_1[s]\) に達すると、制御回路によってスイッチが \(S_2\) 側に切り換わり、積分器には基準電圧 \(-V_r[V]\) が入力される。よって、スイッチ \(S_2\) の期間中の時刻 \(t[s]\) における積分器の出力電圧の大きさは、 \(V_o=V_m-\fbox{(イ)}[V]\) と表される。
積分器の出力電圧 \(V_o\) が0Vになると、電圧比較器がそれを検出する。
\(V_o=0V\) のときの時刻を \(t=T_1+T_2[s]\) とすると、測定電圧は \(V_x=\fbox{(ウ)}[V]\) と表される。
さらに、図2(c)のようにスイッチ \(S_1,S_2\) の各期間 \(T_1[s],T_2[s]\) 中にクロックパルス発振器から出力されるクロックパルス数をそれぞれ \(N_1,N_2\) とすると、 \(N_1\) は既知なので \(N_2\) をカウントすれば、測定電圧 \(V_x\) がディジタル信号に変換される。
ここで、クロックパルスの周期 \(T_s\) は、クロックパルス発振器の動作周波数に \(\fbox{(エ)}\) する。
上記の記述中の空白箇所(ア)、(イ)、(ウ)、(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | \(kV_xT_1\) | \(\displaystyle kV_r(t-T_1)\) | \(\displaystyle \frac{T_2}{T_1}V_r\) | 反比例 |
| (2) | \(kV_xT_1\) | \(kV_rT_2\) | \(\displaystyle \frac{T_2}{T_1}V_r\) | 反比例 |
| (3) | \(\displaystyle k \frac{V_x}{T_1}\) | \(\displaystyle k \frac{V_r}{T_2}\) | \(\displaystyle \frac{T_1}{T_2}V_r\) | 比例 |
| (4) | \(\displaystyle k \frac{V_x}{T_1}\) | \(\displaystyle k \frac{V_r}{T_2}\) | \(\displaystyle \frac{T_1}{T_2}V_r\) | 反比例 |
| (5) | \(kV_xT_1\) | \(\displaystyle kV_r(t-T_1)\) | \(T_1T_2V_r\) | 比例 |
(b)基準電圧が\(V_r=2.0V\)、スイッチ\(S_1\)の期間\(T_1[s]\)中のクロックパルス数が\(N_1=1.0×10^3\)のディジタル直流電圧計がある。
この電圧計を用いて未知の電圧\(V_x[V]\)を測定したとき、スイッチ\(S_2\)の期間\(T_2[s]\)中のクロックパルス数が\(N_2=2.0×10^3\)であった。
測定された電圧\(V_x\)の値[V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)0.5 (2)1.0 (3)2.0 (4)4.0 (5)8.0
答え
(a) 1
(b) 4
解説テキスト リンク
回答解説
(a)解答
① \(\fbox{(ア)}\)を解く
時刻\(0~t_1[s]\)の間の入力電圧\(V_i[V]\)で囲われる面積\(S\)は、
\(S=V_i t_1\) …(1)
問題文から、積分器の出力電圧\(V_o[V]\)は、面積\(S\)に比例し、比例定数\(k\)とすると、
\(V_o=kS=kV_i t_1\) …(2)
となります。
時刻\(T_1\)のときの出力電圧\(V_m\)は、(2)式に測定電圧 \(V_x[V]\)を入力し、
\(V_m=kV_x T_1\) …(3)
となります。
したがって、\((ア)V_m=kV_xT_1[V]\)が答えです。
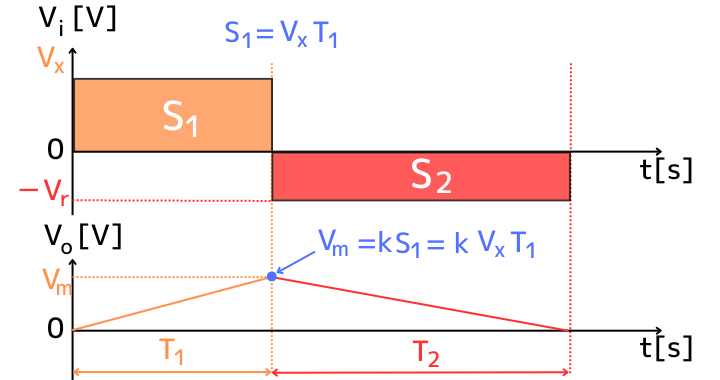
② \(\fbox{(イ)}\)を解く
スイッチが切り替わり、積分器への入力が基準電圧\(-V_r\)となった\(T_2[s]\)の期間を考えます。
スイッチが切り替わった時間が\(T_1[s]\)なので、切り替わり後の経過時間は、\(t-T_1[s]\)となります。
基準電圧\(-V_r[V]\)と、\(t-T_1[s]\)の期間で囲われる面積\(S\)は、
\(S=V_r (t-T_1)\) …(4)
積分器の出力電圧\(V_o[V]\)は、\(V_m\)から減少していきます。
出力電圧の減少量は、面積\(S\)に比例するので、
\(V_o=V_m-kS=V_m-kV_r (t-T_1) \) …(5)
となります。
したがって、\((イ)kV_r (t-T_1)[V]\)が答えです。
③ \(\fbox{(ウ)}\)を解く
問題文から、電圧比較器が検出する\(V_o=0V\) のときの時刻\(t=T_1+T_2[s]\)を(5)式に代入することで、測定電圧\(V_x\)が求まります。
\(V_o=V_m-kV_r (t-T_1) \) …(5)式に、
\(V_m=kV_x T_1\) …(3)と、
\(t=T_1+T_2[s]\)を代入します。
\(V_o=kV_x T_1-kV_r (T_1+T_2-T_1)=kV_x T_1-kV_rT_2 \)
このとき、\(V_o=0V\) なので、
\(kV_x T_1-kV_rT_2=0 \)
⇔\(V_x =\frac{T_2}{T_1}V_r \)
したがって、\((ウ)\frac{T_2}{T_1}V_r[V]\)が答えです。
④ \(\fbox{(エ)}\)を解く
クロックパルスの周期\(T_s[s]\)とクロックパルス発振器の動作周波数\(f_s[Hz]\)の関係式は、
\(\displaystyle T_s=\frac{1}{f_s}\)
なので、クロックパルスの周期\(T_s[s]\)は、クロックパルス発振器の動作周波数に反比例します。
(b)解答
(a)の(ウ)の解答から、測定電圧\(V_x\)は、次式となります。
\(V_x =\frac{T_2}{T_1}V_r \) …(1)
スイッチ\(S_1\)の期間\(T_1\)は、クロックパルス数\(N_1\)と、クロックパルスの周期\(T_s\)から、次式となります。
\(T_1=N_1T_s\) …(2)
同様に、スイッチ\(S_2\)の期間\(T_2\)は、
\(T_2=N_2T_s\) …(3)
(1)式に、(2)(3)式を代入すると、
\(\displaystyle V_x =\frac{N_2T_s}{N_1T_s}V_r=\frac{N_2}{N_1}V_r\) …(4)
(4)式に、問題の条件、\(V_r=2.0V\)、\(N_1=1000\)、\(N_2=2000\)を代入すると、
\(\displaystyle V_x=\frac{2000}{1000}2.0=4.0V\)
したがって、\((4)4.0\)が答えです。
出典元
一般財団法人電気技術者試験センター (https://www.shiken.or.jp/index.html)
令和1年度 第三種電気主任技術者試験 理論科目B問題問18
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント