比例推移とは
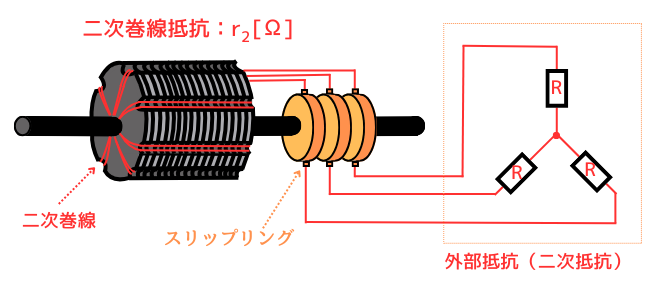
巻線形誘導電動機では、スリップリングを通して二次側に外部抵抗が接続されます。
外部抵抗\(R\)の抵抗値を変化させることで、
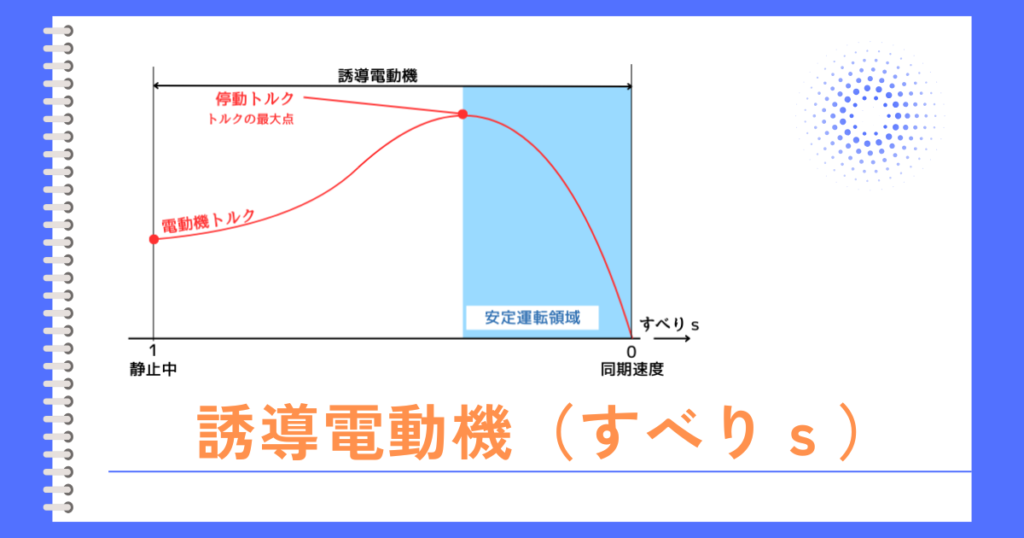
すべり\(s\)-トルク\(T\)の特性曲線を変化させることが出来ます。

二次抵抗は、二次巻線抵抗\(r’_2[Ω]\)と、外部抵抗\(R[Ω]\)の合計で\(r’_2+R\)となります。
\(r’_2+R\)は、\(r’_2\)の\(m\)倍として表せるので、\(mr’_2=r’_2+R\)とも書けます。
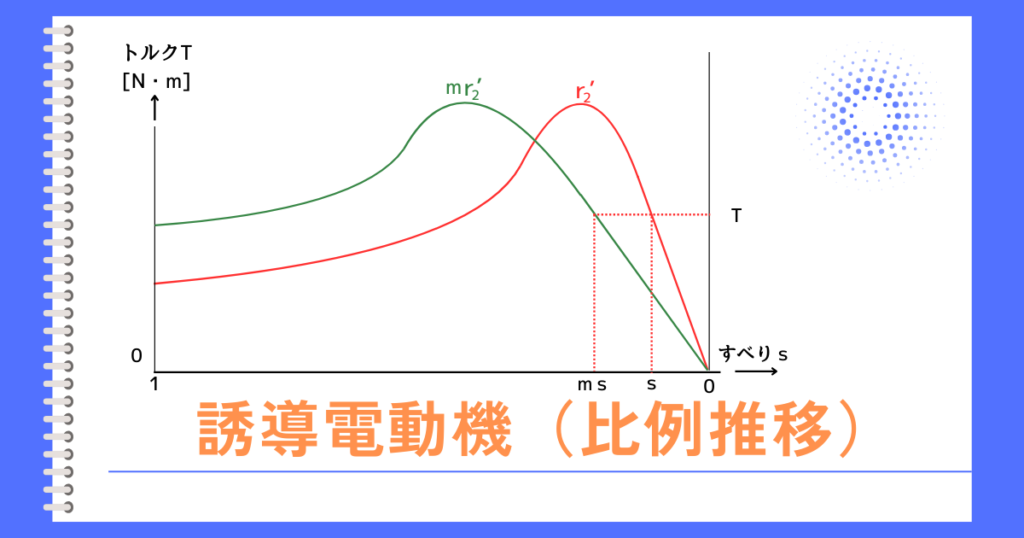
二次抵抗\(r’_2[Ω]\)が\(m\)倍になると、トルク特性曲線は横に\(m\)倍に引き伸ばされた形になります。
つまり、二次抵抗に比例してトルク特性曲線が推移するので、比例推移と呼ばれます。
巻線形誘導機では、比例推移を利用することで、始動特性を改善でき、速度制御もできます。
そのため、大型の誘導電動機に使われることが多いです。
公式
\(\displaystyle \frac{r’_2}{s}=\frac{mr’_2}{ms}=\frac{r’_2+R}{s’}\)
・\(r’_2\):二次巻線抵抗
・\(R\):外部抵抗
・\(s\):外部抵抗が無い(\(R=0\))ときのすべり
・\(s’\):二次抵抗が(\(r’_2+R\))のときのすべり
比例推移の導出
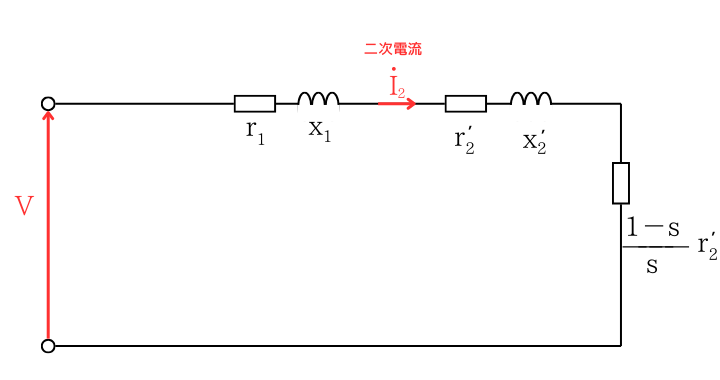
誘導電動機の二次電流の大きさ\(I_2\)は、
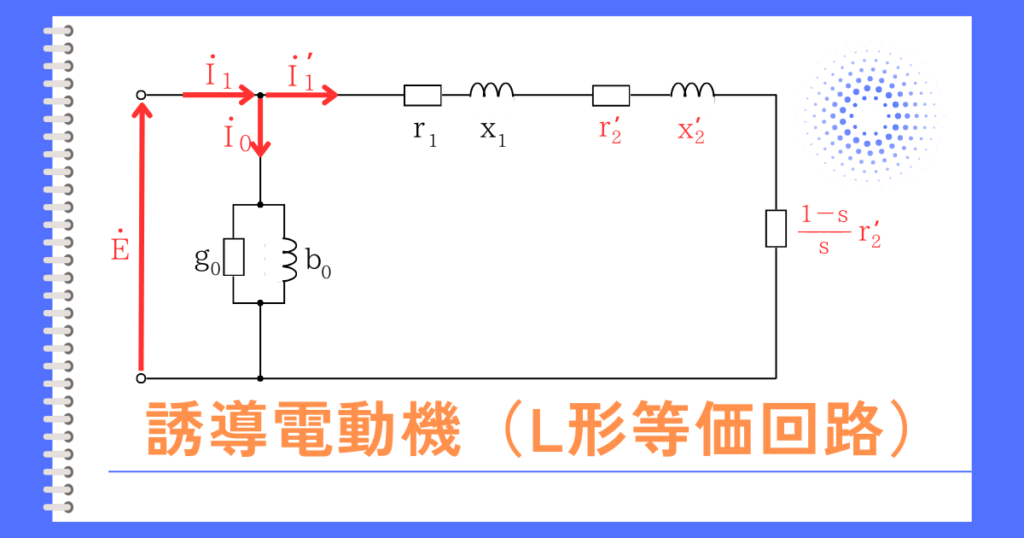
\(\displaystyle I_2=\frac{V}{\sqrt{(r_1+\frac{r’_2}{s})^2+(x_1+x’_2)^2}}\) …①
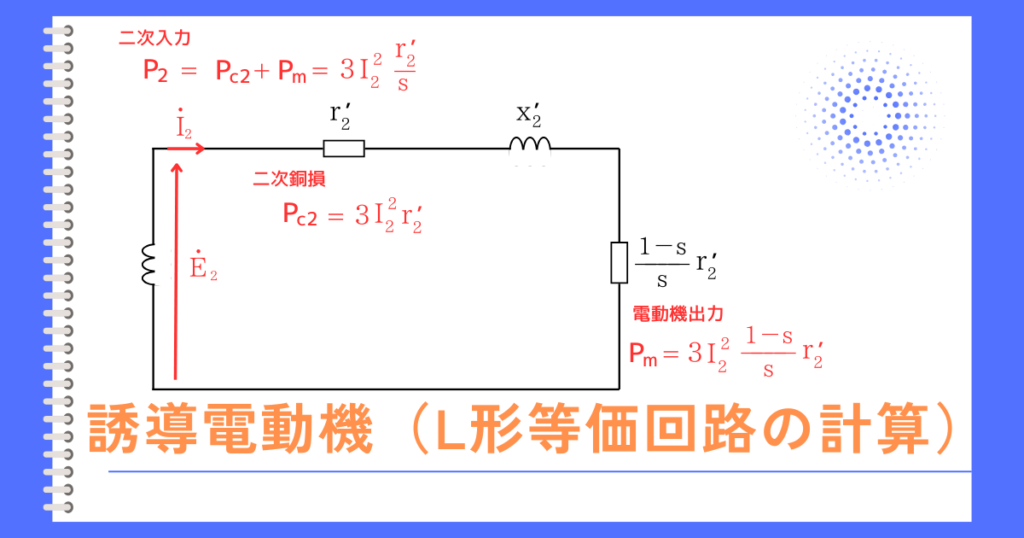
二次入力\(P_2\)は、
\(\displaystyle P_2=3I^2_2 \frac{r’_2}{s}=\frac{3\frac{r’_2}{s}}{(r_1+\frac{r’_2}{s})^2+(x_1+x’_2)^2}V^2\) …②
機械的出力\(P_m\)は、
\(P_2:P_{c2}:P_m=1:s:1-s\)の関係から、
\(P_m=(1-s)P_2\) …③
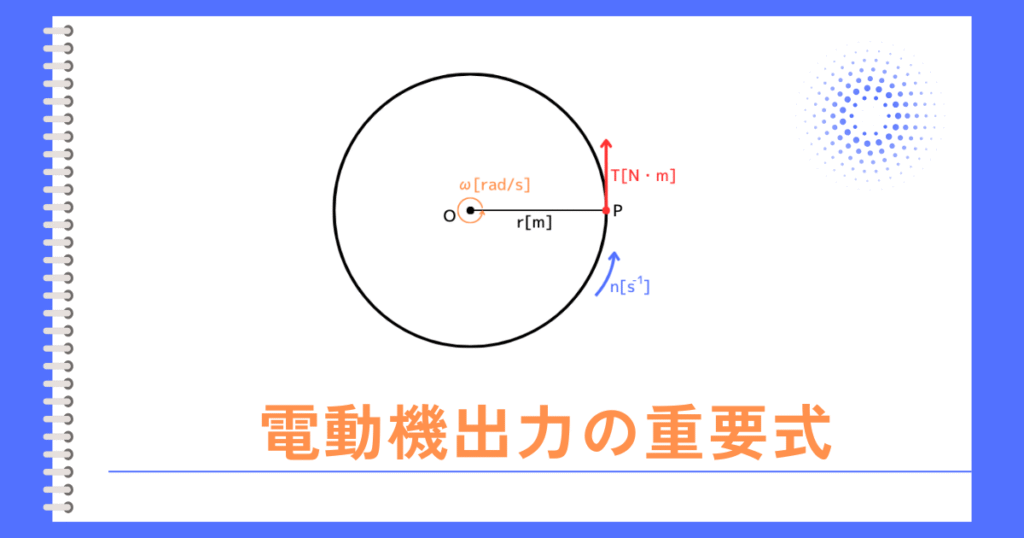
回転角速度\(ω\)は、すべりの定義式から、
\(ω=(1-s)ω_s\) …④
すべりの定義式
\(s=\frac{ω_s-ω}{ω_s}\)
トルク\(T\)は、③・④式から
\(\displaystyle T=\frac{P_m}{ω}=\frac{(1-s)P_2}{(1-s)ω_s}=\frac{P_2}{ω_s}\) …⑤
⑤式に②式を代入すると、
\(\displaystyle T=\frac{3\frac{r’_2}{s}}{(r_1+\frac{r’_2}{s})^2+(x_1+x’_2)^2}\frac{V^2}{ω_s}\) …⑥
⑥式から、トルクの特性式が立式出来ました。
ここからは、すべりによって特性が大きく異なるので、場合分けをして検討していきます。
1.始動直後(\(s=1\))のときを考えます。
この時、抵抗成分よりも漏れリアクタンス\(x_1+x’_2\)が遥かに大きいため、
・\(x_1+x’_2>>r_1+\frac{r’_2}{s}\)
この条件で、⑥式を簡略化します。
\(\displaystyle T=\frac{3\frac{r’_2}{s}}{x_1+x’_2}\frac{V^2}{ω_s}=\frac{3r’_2 V^2}{(x_1+x’_2)sω_s}\) …⑦
⑦式からわかること
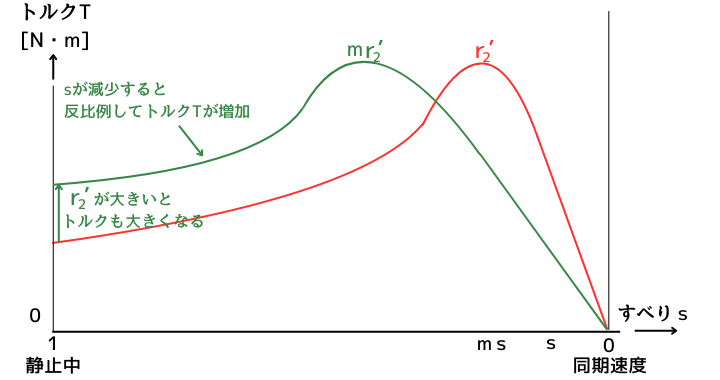
・始動直後(\(s=1\))は、二次抵抗\(r’_2\)とトルク\(T\)が比例します。
➡ 二次抵抗\(r’_2\)が大きいと、始動トルク\(T\)も大きい
➡ 二次抵抗によって始動特性が改善できる
・すべり\(s\)が小さくなるにつれ、反比例してトルクが大きくなっていきます。
2.定格運転時(\(s=0.05\)前後)のときを考えます。
この時、漏れリアクタンス\(x_1+x’_2\)が小さくなり、二次抵抗\(r’_2\)が支配的になるので、次の条件で簡略化できます。
・\(\frac{r’_2}{s}>>r_1\)
・\(\frac{r’_2}{s}>>x_1+x’_2\)
この2つ条件で、⑥式を簡略化します。
\(\displaystyle T=\frac{3\frac{r’_2}{s}}{\left( \frac{r’_2}{s} \right)^2}\frac{V^2}{ω_s}=\frac{3sV^2}{r’_2ω_s}\) …⑧
次に、トルク\(T\)を回転速度に関係なく一定とします。
二次抵抗\(r’_2\)を、\(m\)倍に大きくして\(mr’_2\)としたとき、すべり\(s_1\)が\(s_2\)に変わったとします。
この時の\(s_2\)は、⑧式から次のように求められます。
\(\displaystyle T=\frac{3s_1V^2}{r’_2ω_s}=\frac{3s_2V^2}{mr’_2ω_s}\)
⇔ \(\displaystyle \frac{s_1}{r’_2}=\frac{s_2}{mr’_2}\)
⇔ \(\displaystyle s_2=\frac{mr’_2}{r’_2}s_1=ms_1\) …⑨
⑨式からわかること
二次抵抗\(r’_2\)を、\(m\)倍に大きくすると、すべりも\(m\)倍に大きくなります。
➡比例推移が成り立つことがわかりました。

関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。







コメント