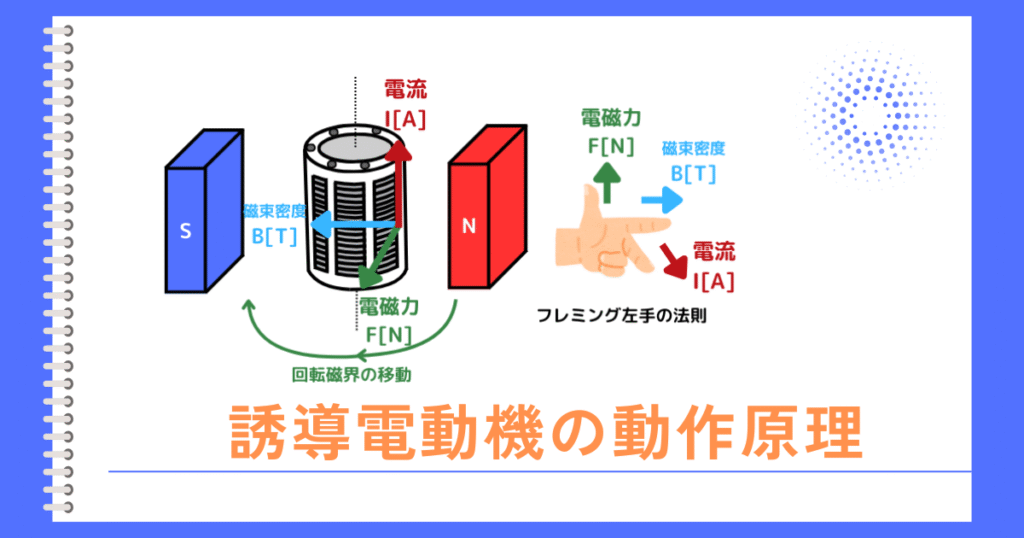
一次周波数制御とは
一次周波数制御は、誘導電動機の速度制御方法の一つです。
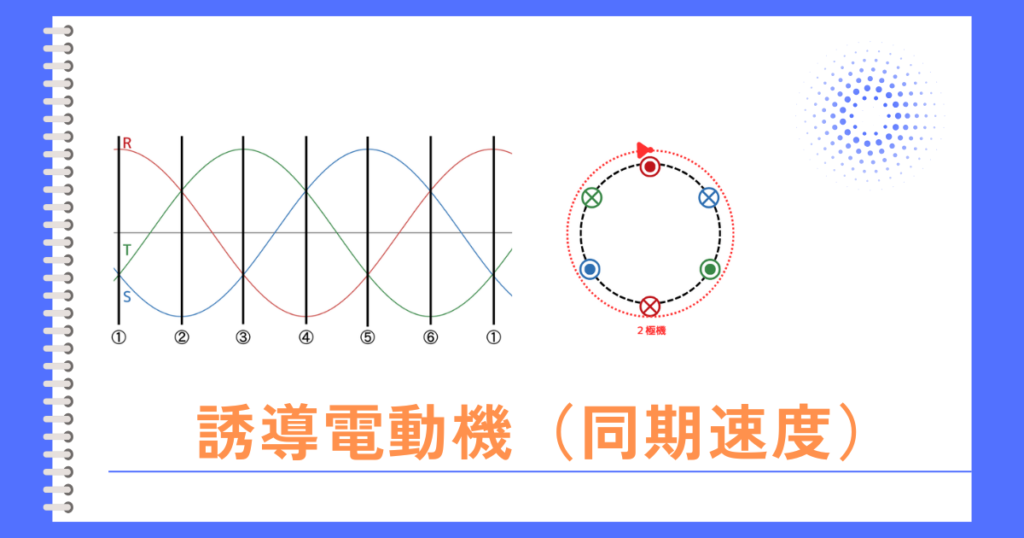
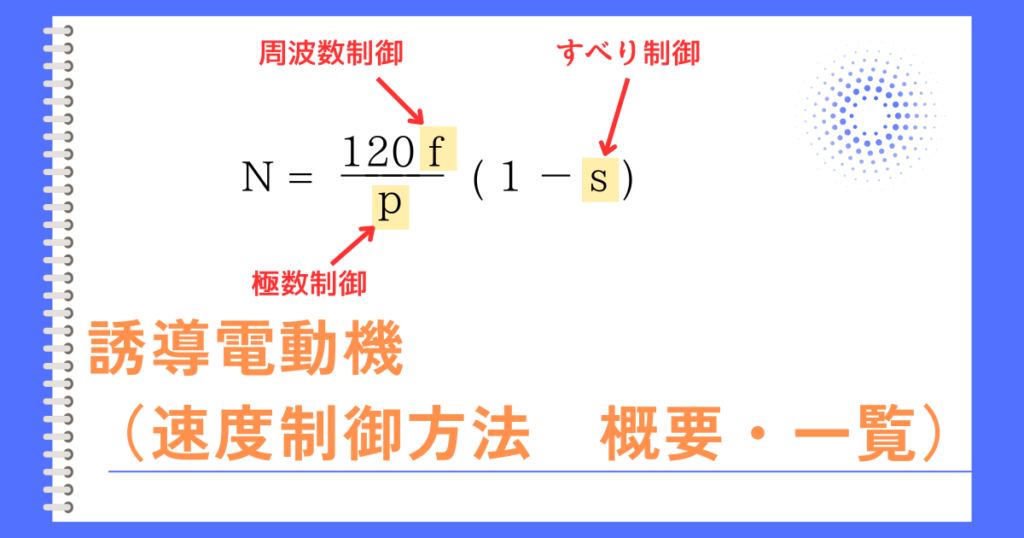
誘導電動機の回転速度\(N[min^{-1}]\)は、
\(N=N_s(1-s)=\frac{120f}{p}(1-s)\)で表され、
\(f\)、\(s\)、\(p\)のどれかを変化させれば回転速度\(N[min^{-1}]\)も変化します。
一次周波数制御は、周波数\(f\)を変化させることで、回転速度を変化させます。
一次周波数制御の方法としては、主に2つあります。
・V/f制御
・ベクトル制御
本頁では、V/f制御について細かく解説していきます。
ベクトル制御については、電験一種で出題されるようなレベルなので、軽く概要について触れる程度にします。
V/f制御
\(V/f\)制御は、電圧\(V\)と周波数\(f\)の比を一定に保って制御することで、誘導機の回転速度を制御する方式です。
電圧\(V\)と周波数\(f\)を同時に操作しなければなりませんが、それをすることが可能なVVVFインバータが普及したため、誘導電動機の速度制御において最も使われる制御方式です。
VVVFは、可変電圧可変周波数(Variable Voltage Variable Frequency)の意味です。
長所
・トルクを保って速度変化させることができる
・効率が良い
\(\frac{V}{f}\)制御する理由
\(N=N_s(1-s)=\frac{120f}{p}(1-s)\)の式から、
周波数\(f\)を変化させれば、同期速度\(N_s\)も比例して変化します。
そのため、周波数\(f\)を操作したいところです。
しかし、周波数\(f\)のみを変化させると、励磁電流\(I_0\)が大きくなってしまい、磁気飽和が起こります。その結果、インダクタンスが低下して過電流が流れることとなり、故障の原因になるという問題があります。
この問題の原因と対策について、回路図と励磁電流の式で示してみます。
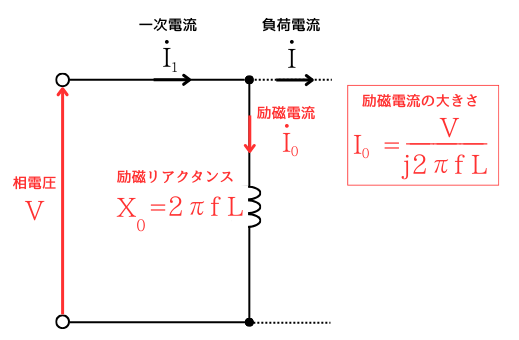
左図は、誘導電動機の励磁回路です。
励磁コンダクタンスは省略し、励磁リアクタンスのみを取り出した回路です。
電源周波数を低下させると、励磁回路の励磁電流\(I_0\)は、
\(I_0≒\frac{V}{2πfL}\)
であるため、周波数\(f\)に反比例して励磁電流\(I_0\)が大きくなります。
\(I_0∝\frac{V}{f}\)であることに着目し、電圧\(V\)と周波数\(f\)の比を一定に保って制御することで、励磁電流\(I_0\)は変わらないため、磁束を一定に保つことができます。
これにより、安定した速度変化をさせることが実現できます。
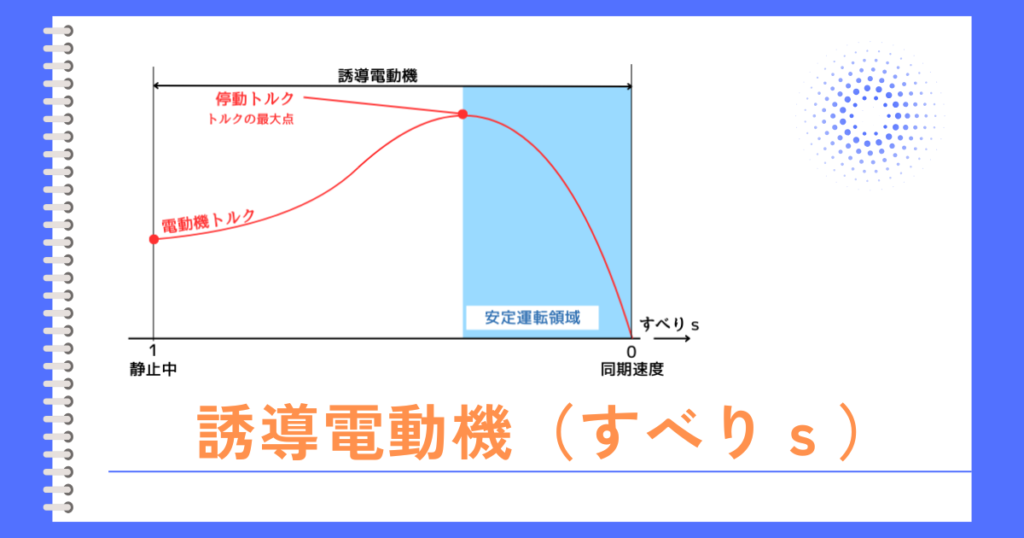
トルク特性
\(\frac{V}{f}\)制御をすることで、トルク\(T\)を一定に保ったまま、速度変化させることができます。
それを示すため、定格運転時の\(\frac{V}{f}\)制御のトルク特性について計算します。
⇩省略
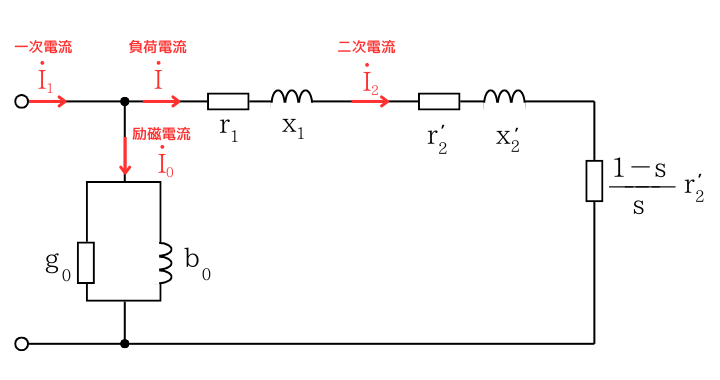
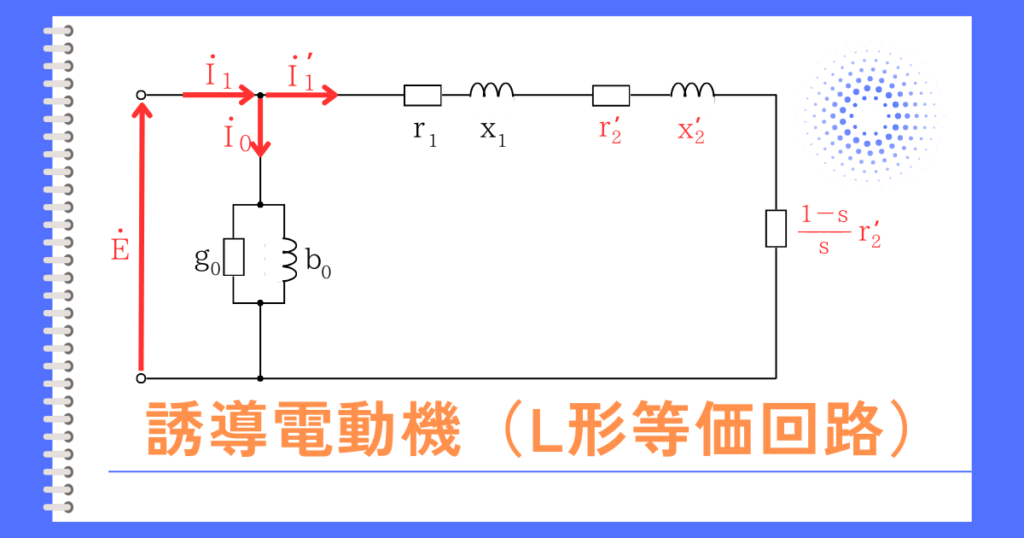
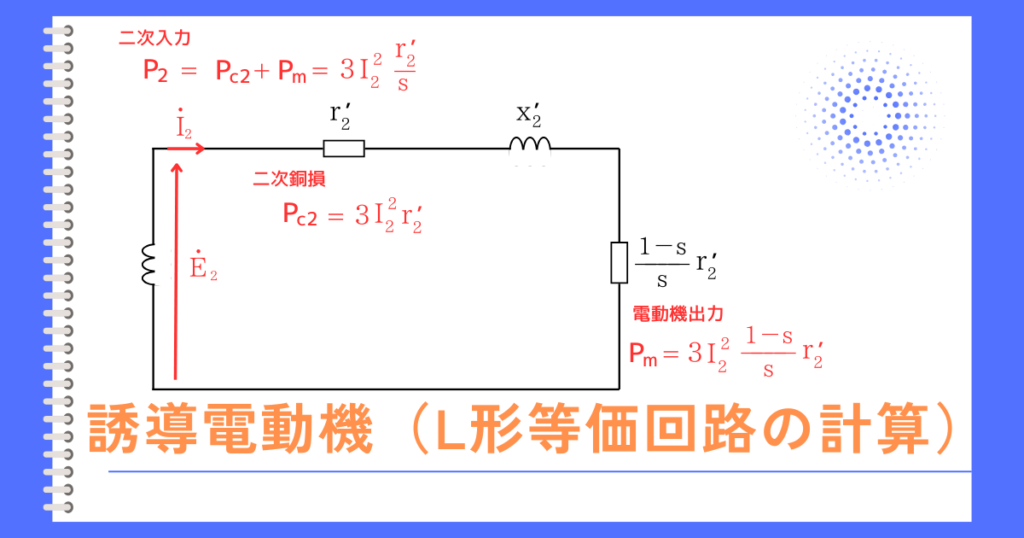
誘導電動機のL形等価回路です。
このとき、二次電流≫励磁電流 なので、励磁回路を省略しても特性をほぼ表現できます。
さらに、
「二次抵抗による電圧降下≫その他の電圧降下」なので、一次抵抗\(r_1\)と漏れリアクタンス\(x_1+x’_2\)を省略しても、おおよその特性を検討できます。
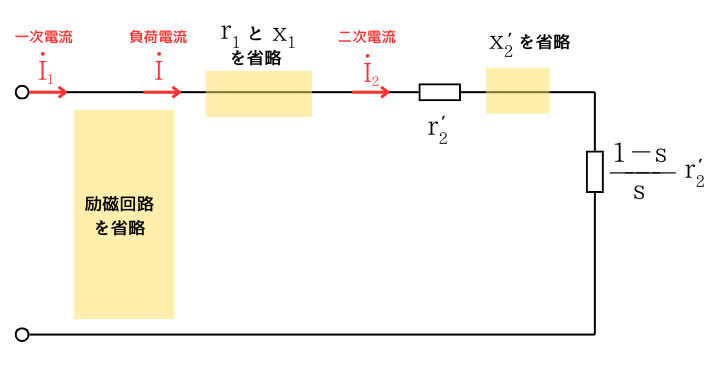
簡略化した回路で、誘導機のトルク特性について検討していきます。
簡略化した回路に関連する、各パラメータを計算していきます。
二次電流の大きさ\(I_2[A]\)は、簡略化した回路図から、
\(\displaystyle I_2=\frac{V}{\frac{r’_2}{s}}=\frac{sV}{r’_2}\) …①
二次入力\(P_2[W]\)は、
\(\displaystyle P_2=3I^2_2 \frac{r’_2}{s}=3\frac{s}{r’_2}V^2\) …②
同期速度\(N_s[min^{-1}]\)は、
\(\displaystyle N_s=\frac{120f}{p}\) …③
同期角速度\(ω_s[rad/s]\)は、③式から、次のように求まります。
\(\displaystyle ω_s=2π\frac{N_s}{60}=\frac{4πf}{p}\) …④
機械的出力を\(P_m[W]\)、軸の回転角速度\(ω[rad/s]\)、トルク\(T[Nm]\)の関係は、
\(P_m=Tω\)
⇔ \(T=\frac{P_m}{ω}=\frac{(1-s)P_2}{(1-s)ω_s}=\frac{P_2}{ω_s}\) …⑤
です。
⑤式に②・④式を代入します。
\(\displaystyle T=\frac{P_2}{ω_s}=\frac{\frac{3s}{r’_2}V^2}{\frac{4πf}{p}}\)
⇔ \(T=\frac{3psV^2}{4πfr’_2}\) …⑥
⑥式のままでは、電源電圧\(V[V]\)と周波数\(f[Hz]\)が変化したときの二次電流\(I_2[A]\)がわからないので、少し変形します。
\(T=\frac{3p}{4π}・\frac{V}{f}・\frac{sV}{r’_2}=\frac{3p}{4π}・\frac{V}{f}・I_2\) …⑦
⑦式の不要な定数をまとめて\(k\)とすると、
\(T=k\frac{V}{f}I_2\) …⑧
となり、トルク\(T\)は、\(\frac{V}{f}\)と、二次電流\(I_2\)に比例することがわかります。
このことから、\(\frac{V}{f}\)を一定に保つように制御することで、二次電流・トルクを一定に保ったまま、速度制御することができることがわかりました。
ベクトル制御
誘導電動機のベクトル制御とは、三相電流(\(i_u,i_v,i_w\))を回転座標系に変換し、磁束を発生する電流成分\(i_d\)と、トルクを発生する電流成分\(i_q\)を数学的に計算して分解し、それぞれの電流成分を独立して制御する方式です。
長所
応答速度が速い
低速でも高トルクを得られる
高精度な速度制御ができる
短所
演算量が多く高性能な制御器が必要
パラメータ調整が難しい
機器・メンテナンスコストが高い
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。







コメント