概要
交流回路の電力、電圧、電流、インピーダンスは三角関数（sinθ、cosθ）で表されますが、計算が大変なので簡略する方法としてフェーザ表示を使います。
本ページでは、三角関数とフェーザ表示の関係を紹介した後、フェーザ表示の計算と、複素電力について紹介していきます。
三角関数から複素数への変換
①複素数平面の虚軸成分と、三角関数のsin成分の対応
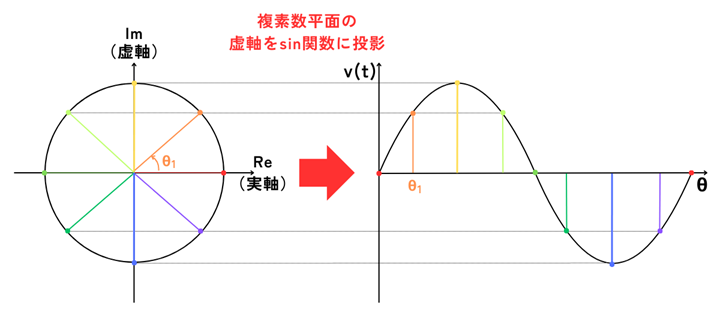
複素数平面の虚軸の成分の大きさを三角関数に反映させると、
電圧はjv(t)=jV_msinθ
と表されます。
②複素数平面の実軸成分と、三角関数のcos成分の対応
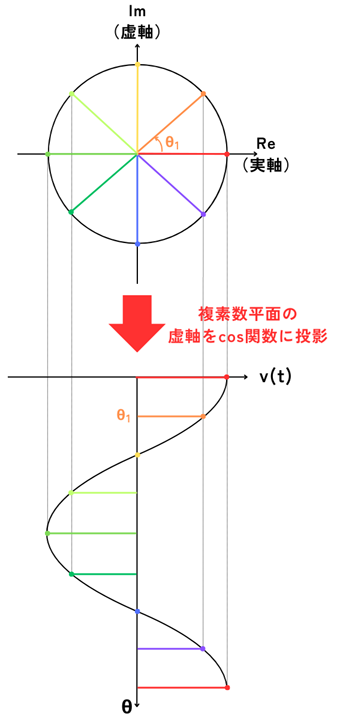
複素数平面の実軸の成分の大きさを三角関数に反映させると、
電圧はv(t)=V_mcosθ
と表されます。
③実軸・虚軸をまとめて直交座標表示で示す
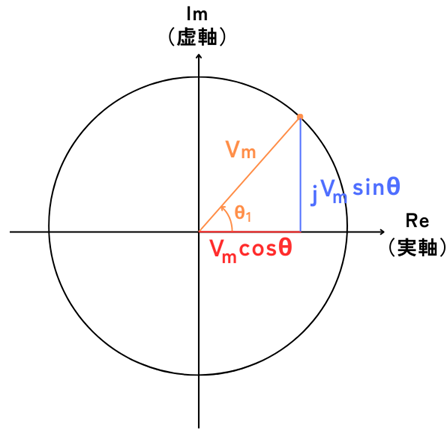
上記の実軸・虚軸成分をまとめ、交流電圧を直交座標表示で示すと
v(t)=V_m(cosθ+jsinθ)
と表すことができます。
④オイラーの公式を使用して三角関数を複素指数関数に変換
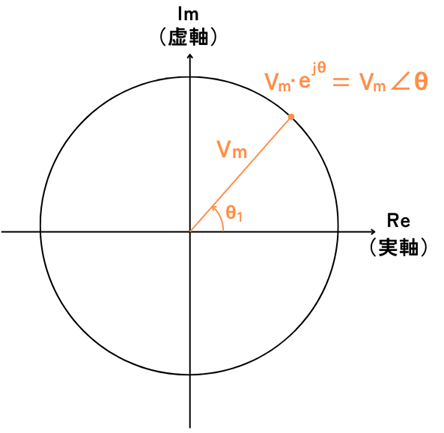
複素指数関数であるe^{jθ}と、三角関数をつなげる式であるオイラーの公式
e^{jθ}=(cosθ+jsinθ)
を使い、直交座標表示の電圧を極座標表示に変換すると、
v(t)=V_me^{jθ}
と表すことができます。
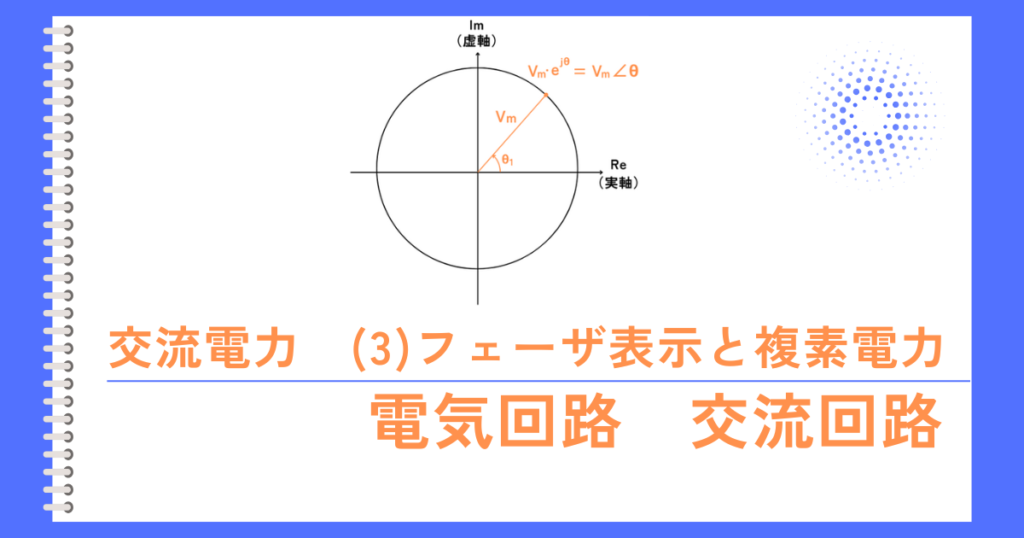
V_me^{jθ}と、指数表示で表記するのは手間なので、V_m∠θと表記することをフェーザ表示と呼びます。
フェーザ表示の電力
フェーザ表示の計算
三角関数で表すことが出来るものを、何故わざわざフェーザ表示にするかというと、計算が非常に簡単になるためです。
その計算方法は、フェーザで表記された電圧、電流、インピーダンスの計算は、大きさの計算と、位相角の計算の２つを別々に分けて計算します。
フェーザ表示の計算方法
・大きさの計算
普通のオームの法則の通りに計算します。
・位相角の計算
乗算の場合は位相角を加算します。除算の場合は位相角を減算します。
フェーザの計算の具体例
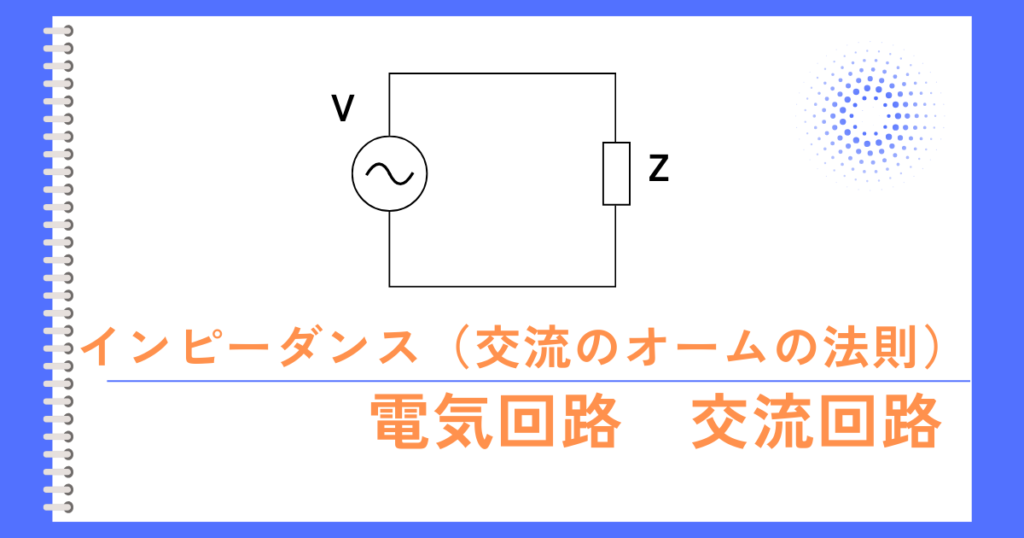
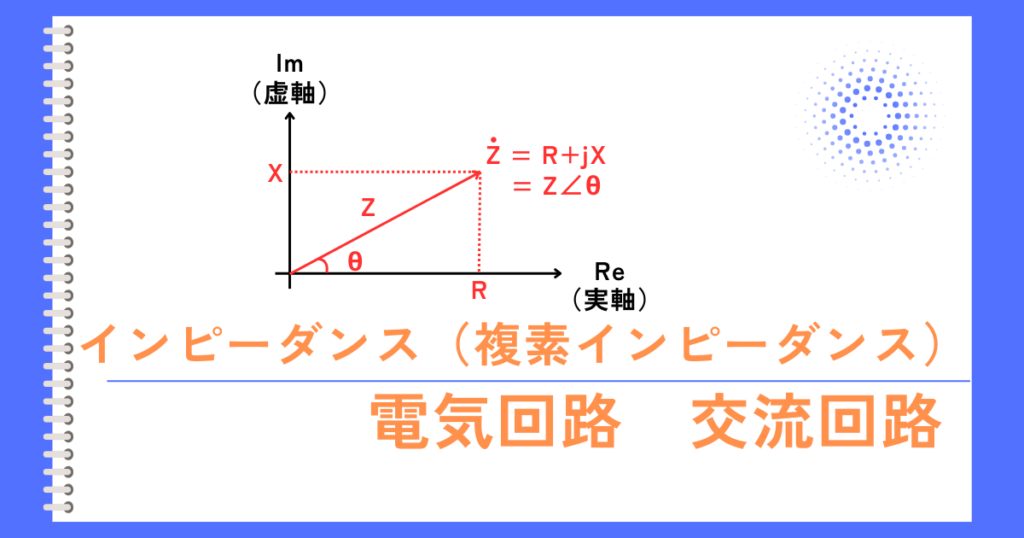
電圧\dot{V}=V∠θ_v、電流\dot{I}=I∠θ_i、インピーダンス\dot{Z}=Z∠θ_zとしたとき、オームの法則の式は、次のように表されます。
・電圧\dot{V}
\dot{V}=\dot{I}・\dot{Z}
➡ V∠θ_v=I∠θ_i・Z∠θ_z=IZ∠(θ_i+θ_z)
・電流\dot{I}
\dot{I}=\frac{\dot{V}}{\dot{Z}}
➡ I∠θ_i=\frac{V∠θ_v}{Z∠θ_z}=\frac{V}{Z}∠(θ_v-θ_z)
・インピーダンス\dot{Z}
\dot{Z}=\frac{\dot{V}}{\dot{I}}
➡ Z∠θ_z=\frac{V∠θ_v}{I∠θ_i}=\frac{V}{I}∠(θ_v-θ_i)
フェーザの位相角の計算の原理
フェーザ表示の電圧・電流・インピーダンスの計算は、複素指数関数の乗算・除算を行っています。
複素指数関数の乗算・除算は、次のように計算されます。
乗算：e^{jA}・e^{jB}=e^{j(A+B)}
フェーザに戻すと ➡ e^{j(A+B)}=e∠(A+B)
除算：\frac{e^{jA}}{e^{jB}}=e^{j(A-B)}
フェーザに戻すと ➡ e^{j(A-B)}=e∠(A-B)
フェーザ表示の裏でこの計算がされていることによって、フェーザ表示の位相角の加減算が成り立っています。
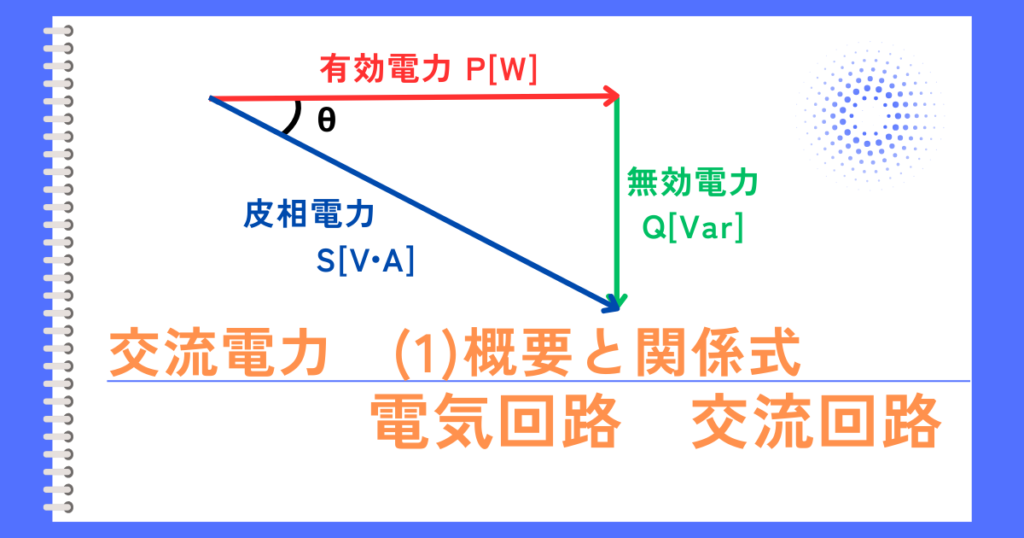
フェーザ表示の皮相電力\dot{S}
フェーザで表示された皮相電力\dot{S}は、電圧\dot{V}=V∠θ_v、電流\dot{I}=I∠θ_iとしたとき、共役複素数を使って次のように表記されます。
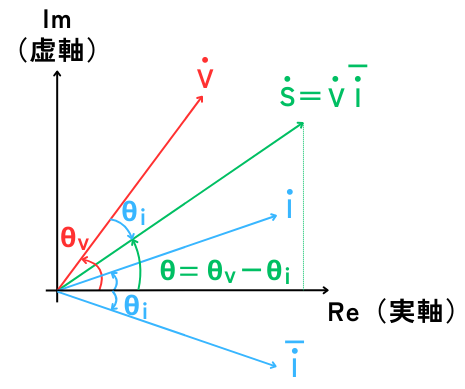
\begin{array}{l} \dot{S}&=&\dot{V}・\bar{\dot{I}}\\ &=&V∠θ_v・I∠-θ_i\\ &=&VI∠(θ_v-θ_i)\\ &=&VI∠θ \end{array}
※θ=θ_v-θ_iとしました。
電力の位相は、右のリンクページで証明しているとおり、θ_vと、θ_iの位相差角θ=θ_v-θ_iが、電力の位相θとなります。
共役複素数を使用せずに、単純に電圧と電流を乗算して\dot{S}=\dot{V}・\dot{I}とした場合、θ_vと、θ_iは加算されるため、θ=θ_v+θ_iとなってしまいます。
こうなると、電力の正しい位相を得ることができなくなってしまいます。
そこで、共役複素数を使い\dot{S}=\dot{V}・\bar{\dot{I}}とすると、電流の位相は-θ_iとなるため、電圧と電流の位相差角θ=θ_v-θ_iを得ることが出来ます。
このことから、電力を計算するときは、共役複素数を使う必要があるのです。
共役複素数の取り方
前例では、電流の共役複素数を取り、\dot{S}=\dot{V}・\bar{\dot{I}} としました。
それでは、電流ではなく、電圧の共役複素数を取り、\dot{S}=\bar{\dot{V}}・\dot{I} とした場合はどうなるでしょうか？
結論
・\dot{S}=\dot{V}・\bar{\dot{I}}の複素電力\dot{S}は、遅れ無効電力が正となります。
・\dot{S}=\bar{\dot{V}}・\dot{I}の複素電力\dot{S}は、進み無効電力が正となります。
電力の進み無効電力、遅れ無効電力とは何か
・進み無効電力
電流の位相Iが電圧の位相Vよりも進んでいるときに発生する電力です。
・遅れ無効電力
電流の位相Iが電圧の位相Vよりも遅れているときに発生する電力です。
・\dot{S}=\dot{V}・\bar{\dot{I}}の複素電力\dot{S}が、遅れ無効電力が正となる理由
複素電力の位相θ=θ_v-θ_iが正となる条件は、（θ_v>θ_i）のときです。
つまり、電流の位相θ_iが電圧の位相θ_vよりも遅れているときです。
このことから、遅れ無効電力が発生しているときに、複素電力\dot{S}が正となるため、遅れ無効電力が正となると言えます。
・\dot{S}=\bar{\dot{V}}・\dot{I}の複素電力\dot{S}が、進み無効電力が正となる理由
複素電力の位相θ=θ_i-θ_vが正となる条件は、（θ_i>θ_v）のときです。
つまり、電流の位相θ_iが電圧の位相θ_vよりも進んでいるときです。
このことから、進み無効電力が発生しているときに、複素電力\dot{S}が正となるため、進み無効電力が正となると言えます。
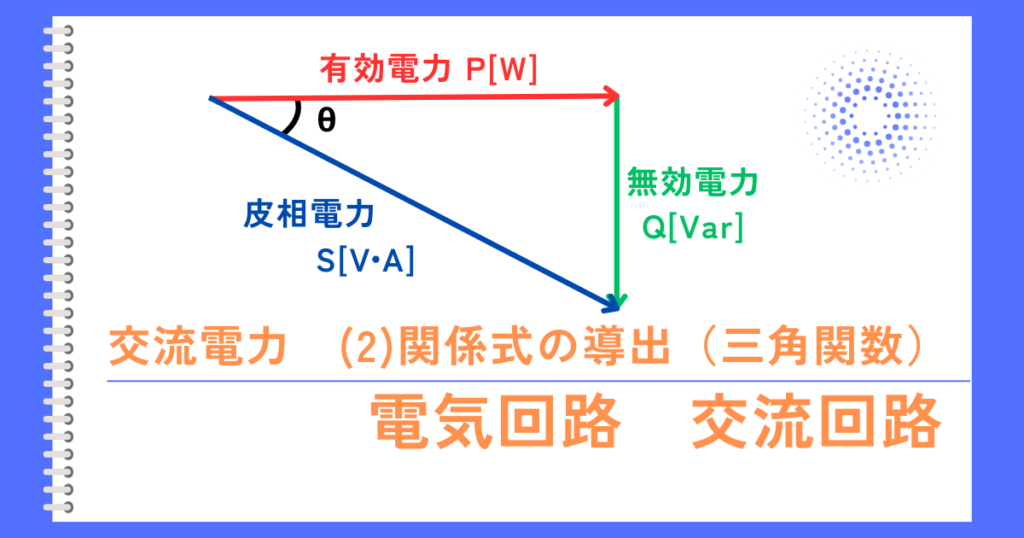
\dot{S}=\dot{V}・\bar{\dot{I}}と、\dot{S}=\bar{\dot{V}}・\dot{I}を図示すると下図のようになります。
\dot{S}=\dot{V}・\bar{\dot{I}}のときの位相の関係図
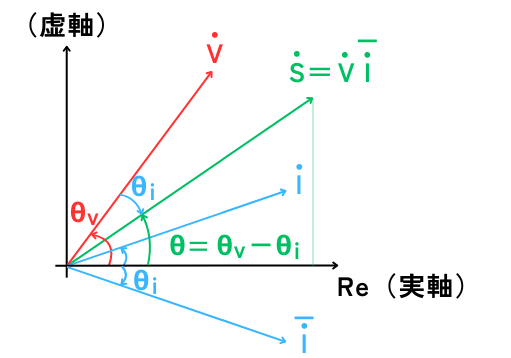
\dot{I}が、\dot{V}よりも遅れているとき（遅れ無効電力が発生しているとき）、\dot{S}の無効電力は正となります。
\dot{S}=\bar{\dot{V}}・\dot{I}のとき位相の関係図
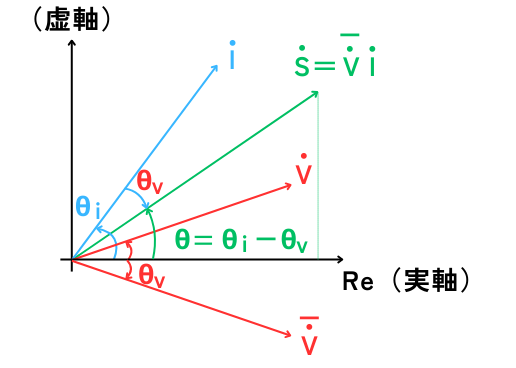
\dot{I}が、\dot{V}よりも進んでいるとき（進み無効電力が発生しているとき）、\dot{S}の無効電力は正となります。
関連記事（その他）
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験３種過去問マスタを使って電験３種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。
コメント