概要
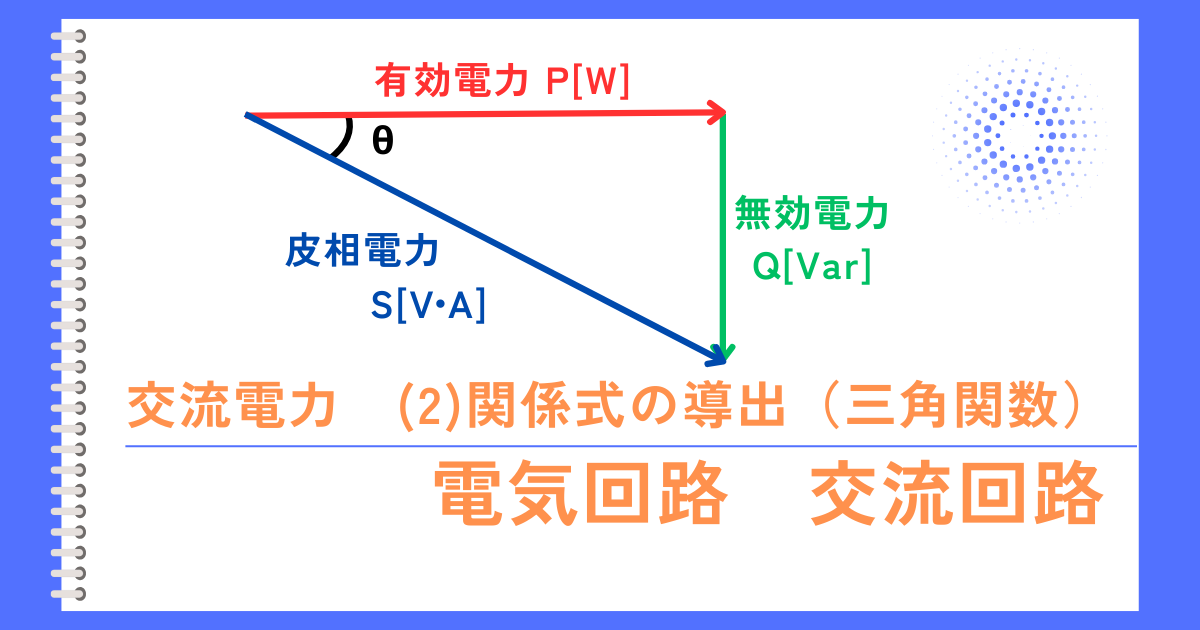
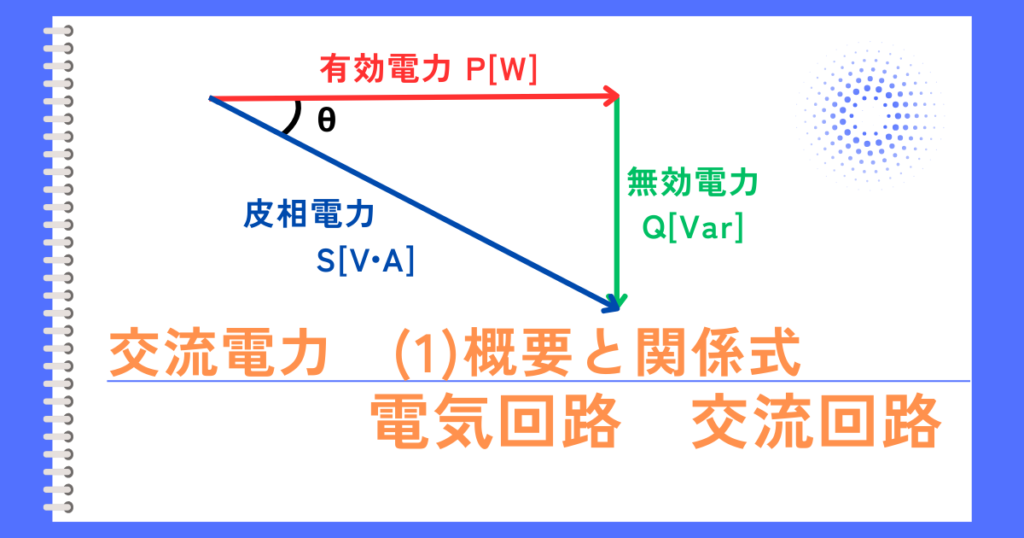
交流回路の電力は、皮相電力\(S[V・A]\)、有効電力\(P[W]\)、無効電力\(Q[Var]\)の3種類があります。
この3つの電力の関係と力率は、左図のリンクの概要説明ページで、
・\(S^2=P^2+Q^2\)
・\(P=VIcosθ\)
・\(Q=VIsinθ\)
・\(cosθ=\frac{P}{S}\)
で示されることを解説しました。
このページでは、三角関数で表される瞬時電圧\(v(t)\)、瞬時電流\(i(t)\)、瞬時電力\(p(t)\)を示し、それぞれ有効電力\(P[W]\)、\(Q[Var]\)、\(S[V・A]\)を計算した結果、上記の数式が出る事を示していきます。
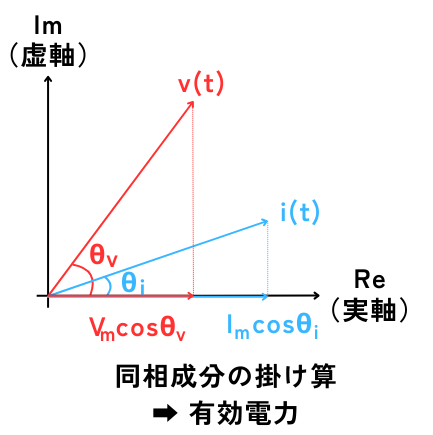
有効電力\(P[W]\)
有効電力\(P\)は電圧と電流の位相差角\(θ\)の実数部分\(cosθ\)
瞬時電圧\(v(t)\)の位相\(θ_v\)と、瞬時電流\(i(t)\)の位相\(θ_i\)の位相差角を\(θ=θ_v-θ_i\)としたとき、その位相差角の実数部分(\(cosθ\))が有効電力\(P[W]\)となります。
\(P=V_r・I_rcosθ=V_r・I_rcos(θ_v-θ_i)\)
\(V_r\)、\(I_r\)は電圧・電流の実効値です。
(1)電力の瞬時値\(p(t)\)の導出
交流電源の電圧・電流の瞬時値を\(v(t)\)・\(i(t)\)とします。
\(\begin{eqnarray}
\left\{\begin{array}{l}
v(t)=V_mcos(ωt+θ_v) \\
i(t)=I_mcos(ωt+θ_i)
\end{array}
\right.
\end{eqnarray}\)
\(V_m\)・\(I_m\)は電圧・電流の波高値。ωは角周波数。\(θ_v\)・\(θ_i\)は基準に対する電圧・電流の位相です。
このとき、瞬時電力\(p(t)\)は次のように展開できます。
\(\begin{eqnarray}
p(t)&=&v(t)・i(t) \\
&=&V_mI_mcos(ωt+θ_v)・cos(ωt+θ_i) …①\\
\\
&=&\frac{V_mI_m}{2} \{cos(2ωt+θ_v+θ_i)+cos(θ_v-θ_i) \} …②\\
\\
&=&\frac{V_m}{\sqrt{2}}・\frac{I_m}{\sqrt{2}} \{ cos(2ωt+θ_p)+cos(θ_v-θ_i) \} …③\\
\\
&=&V_rI_r \{cos(2ωt+θ_p)+cos(θ_v-θ_i) \} …④\\
&=&V_rI_r \{cos2ωt・cosθ_p-sin2ωt・sinθ_p+cos(θ_v-θ_i) \} …⑤\\
\end{eqnarray}\)
補足
①式➡②式は、加法定理の逆変換を使っています。
\(cosα・cosβ=\frac{cos(α+β)+cos(α-β)}{2}\)
②式➡③式は、\(θ_p=θ_v+θ_i\)としてまとめています。
③式➡④式は、電圧・電流の波高値と実効値(rms)の関係式でまとめています。
\(V_r=\frac{V_m}{\sqrt{2}}\)、\(I_r=\frac{I_m}{\sqrt{2}}\)
④式➡⑤式は、加法定理で展開しています。
(2)有効電力\(P\)の導出
有効電力\(P\)は、瞬時電力\(p(t)\)の1サイクルの平均です。
1サイクル迎えた時の時間を\(T[s]\)とします。
\(\begin{eqnarray}
P&=&\frac{1}{T}\int_0^T p(t)dt \\
\\
&=&\frac{1}{T}\int_0^T V_rI_r \{cos2ωt・cosθ_p-sin2ωt・sinθ_p+cos(θ_v-θ_i)\}\\
\\
&=&\frac{V_rI_r}{T} \left[ \frac{1}{2ω}sin2ωt・cosθ+\frac{1}{2ω}cos2ωt・sinθ+tcos(θ_v-θ_i) \right] ^{ T}_{ 0}\\
\\
&=&\frac{V_rI_r}{T}Tcos(θ_v-θ_i) \\
\\
&=& V_rI_rcos(θ_v-θ_i) \\
&=& V_rI_rcosθ \\
\end{eqnarray}\)
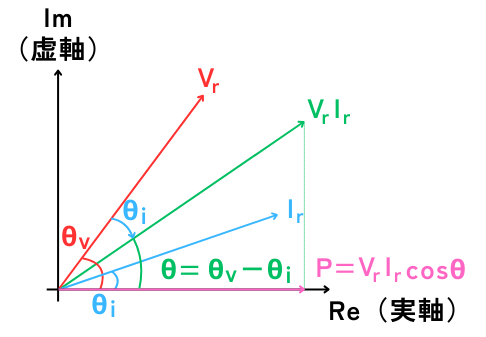
以上より、有効電力\(P[W]\)は、
\(P=V_rI_rcos(θ_v-θ_i)=V_rI_rcosθ\)
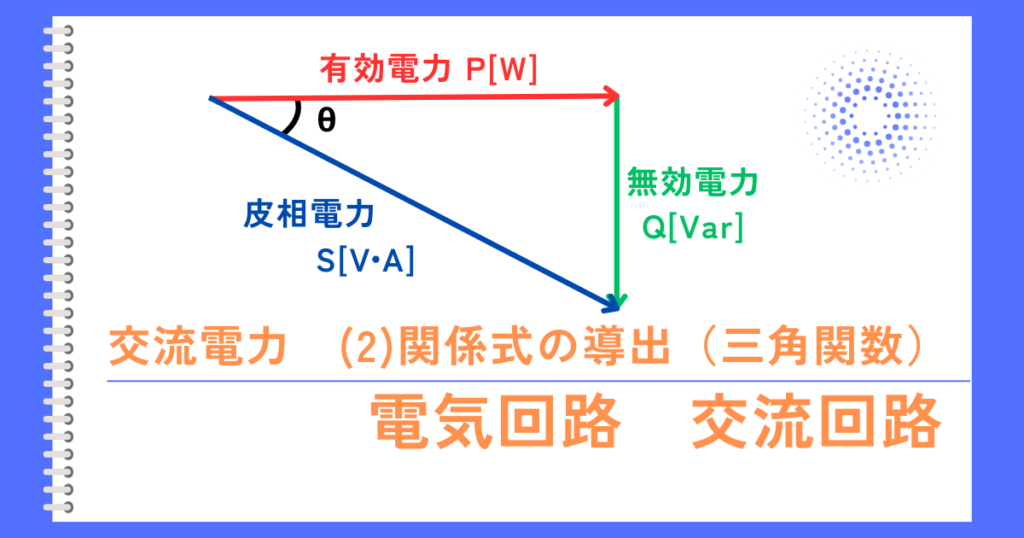
となり、実効電圧\(V_r\)、実効電流\(I_r\)、有効電力\(P\)を図に示すと、左図の通りです。
これにより、実効電圧\(V_r\)の位相\(θ_v\)と、実効電流\(I_r\)の位相\(θ_i\)の位相差角\(θ=θ_v-θ_i\)で表されることがわかります。
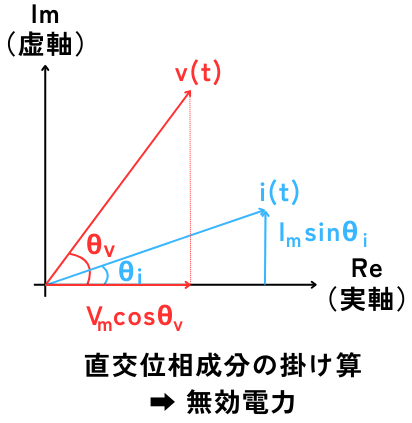
無効電力\(Q[Var]\)
無効電力\(Q\)は電圧と電流の位相差角\(θ\)の虚数部分\(sinθ\)
瞬時電圧\(v(t)\)の位相\(θ_v\)と、瞬時電流\(i(t)\)の位相\(θ_i\)の位相差角を\(θ=θ_v-θ_i\)としたとき、その位相差角の虚数部分(\(sinθ\))が無効電力\(Q[W]\)となります。
\(Q=V_r・I_rsinθ=V_r・I_rsin(θ_v-θ_i)\)
\(V_r\)、\(I_r\)は電圧・電流の実効値です。
有効電力は、電圧も電流も両方とも\(cosωt\)で、同相成分の掛け算でした。
電圧が\(cosωt\)、電流が\(sinωt\)の直交位相成分の掛け算をして有効電力と同様に計算すると、無効電力が求まります。
(1)電圧・電流の直交位相成分の電力の瞬時値\(q(t)\)の導出
交流電源の電圧・電流の瞬時値を\(v(t)\)・\(i(t)\)とします。
\(\begin{eqnarray}
\left\{\begin{array}{l}
v(t)=V_mcos(ωt+θ_v) \\
i(t)=I_msin(ωt+θ_i)
\end{array}
\right.
\end{eqnarray}\)
瞬時電力\(q(t)\)を展開していきます。
\(\begin{eqnarray}
q(t)&=&v(t)・i(t) \\
&=&V_mI_mcos(ωt+θ_v)・sin(ωt+θ_i) \\
\\
&=&\frac{V_mI_m}{2} \{sin(2ωt+θ_v+θ_i)+sin(θ_v-θ_i) \} \\
\\
&=&V_rI_r \{ sin2ωtcosθ_p+cos2ωtsinθ+sin(θ_v-θ_i) \}
\end{eqnarray}\)
※\(θ_p=θ_v+θ_i\)としています。
(2)無効電力\(Q\)の導出
無効電力\(Q\)は、瞬時電力\(q(t)\)の1サイクルの平均です。
1サイクル迎えた時の時間を\(T[s]\)とします。
\(\begin{eqnarray}
Q&=&\frac{1}{T}\int_0^T q(t)dt \\
\\
&=&\frac{1}{T}\int_0^T V_rI_r \{sin2ωt・cosθ_p-cos2ωt・sinθ_p+sin(θ_v-θ_i)\}\\
\\
&=&\frac{V_rI_r}{T} \left[ -\frac{1}{2ω}cos2ωt・cosθ+\frac{1}{2ω}sin2ωt・sinθ+tsin(θ_v-θ_i) \right] ^{ T}_{ 0}\\
\\
&=&\frac{V_rI_r}{T}Tsin(θ_v-θ_i) \\
\\
&=& V_rI_rcos(θ_v-θ_i) \\
&=& V_rI_rcosθ \\
\end{eqnarray}\)
※\(θ=θ_v-θ_i\)としています。
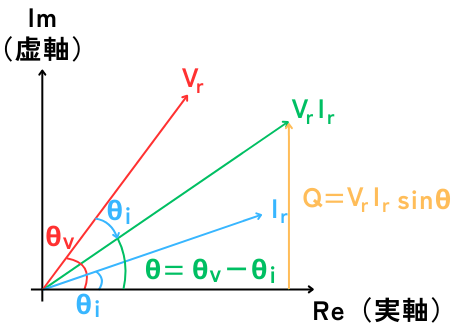
以上より、\(q(t)=v(t)・i(t)\)としたとき、瞬時電力\(q(t)\)の1サイクルの平均電力計算をしていくと、無効電力\(Q[Var]\)が求まります。
\(Q=V_rI_rsin(θ_v-θ_i)=V_rI_rsinθ\)
と、求まります。
実効電圧\(V_r\)、実効電流\(I_r\)、無効電力\(Q\)を図に示すと、左図の通りです。
皮相電力\(S[V・A]\)
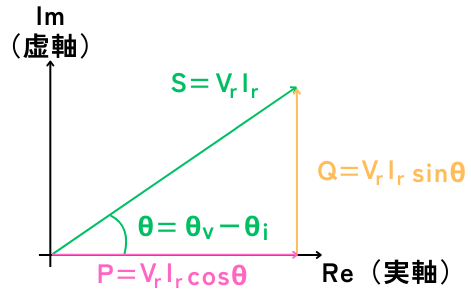
皮相電力\(S\)の大きさは、三平方の定理から
\(S^2=P^2+Q^2\)
です。
力率\(cosθ\)は、送られた電力である皮相電力\(S\)のうち、実際に働いた電力である有効電力\(P\)の割合を示す比率です。
皮相電力\(S\)と有効電力\(P\)の比なので、力率の式は、
\(cosθ=\frac{P}{S}\)
です。
皮相電力\(S\)、有効電力\(P\)、無効電力\(Q\)の関係を図に示すと、左図の通りです。
まとめ
この3つの電力の関係と力率の関係式
・\(S^2=P^2+Q^2\)
・\(P=VIcosθ\)
・\(Q=VIsinθ\)
・\(cosθ=\frac{P}{S}\)
を、瞬時電圧、瞬時電流から導出しました。
三角関数と積分を使って電力を表す方法は、面倒くさいため、これらの関係が複素数で表すことが出来る事を利用して、複素数で計算する方法を次のページで示していきます。
関連記事(その他)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント