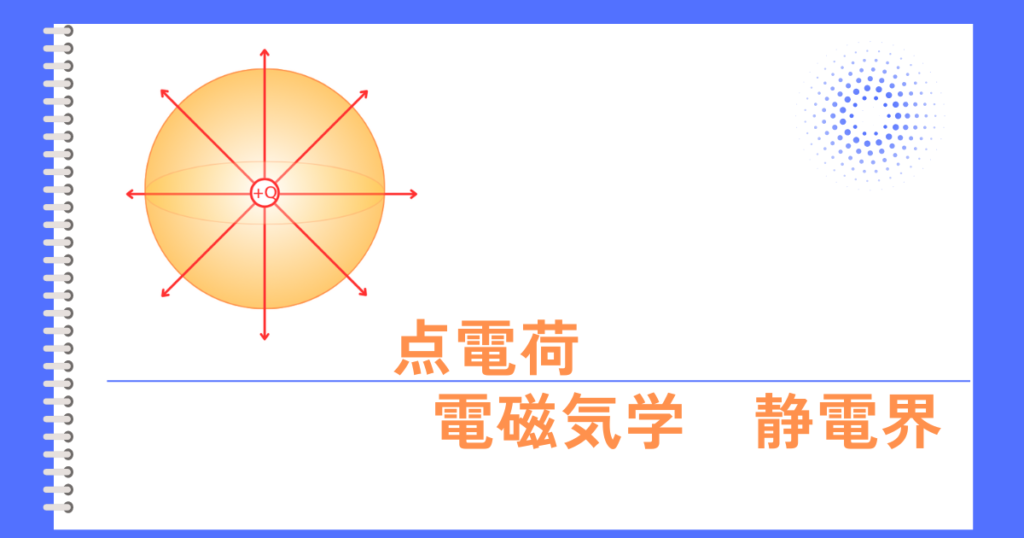
点電荷とは
大きさを無視できるような極めて小さい物体に帯電している電荷を点電荷と呼びます。
点電荷について考えることで、電気力線の広がりや、静電気力等の基本的な性質がわかります。
公式一覧
点電荷に関連する公式をまとめると次の通りです。
電界の式(ガウスの法則)
\(\displaystyle E=\frac{Q}{4πε_0r^2}\)
クーロン力(静電気力)の大きさ
\(\displaystyle F=\frac{qQ}{4πε_0r^2}\)
電位の式
\(\displaystyle V=\frac{Q}{4πε_0r}\)
静電エネルギーの式
\(\displaystyle W=qV = \frac{qQ}{4πε_0r}\)
関係式の一覧マップ
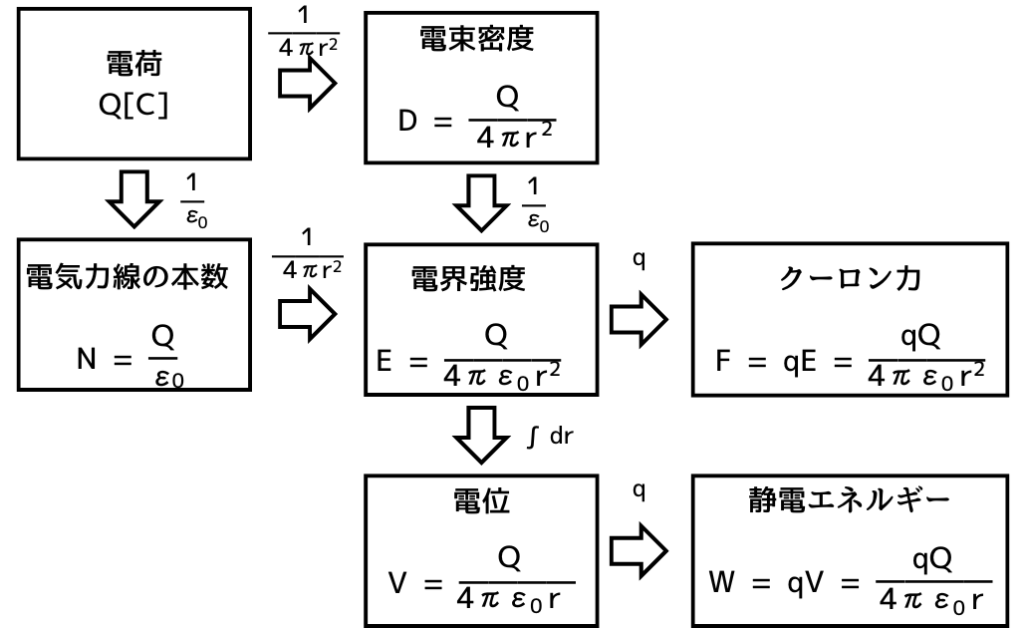
電界強度\(E[V/m]\)
電界強度Eの大きさ(ガウスの法則)
コンデンサの電界強度\(E[V/m]\)は
\(\displaystyle E=\frac{Q}{4πε_0r^2}\)
点電荷の電界強度\(E[V/m]\)の式の証明
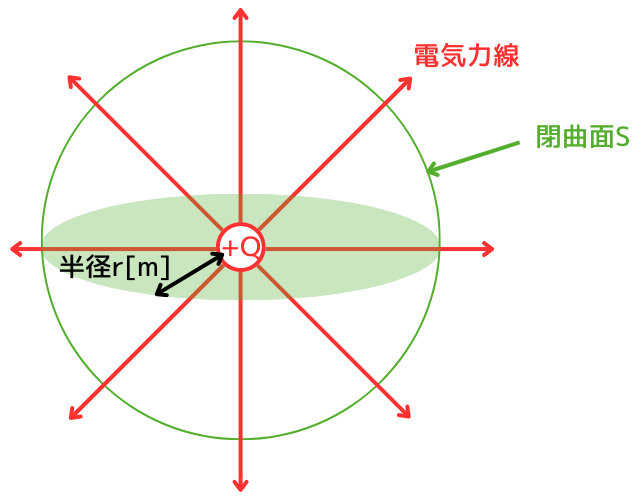
ガウスの法則の式を示します。
\(\displaystyle \oint_S EdS=\frac{Q}{ε_0}\)
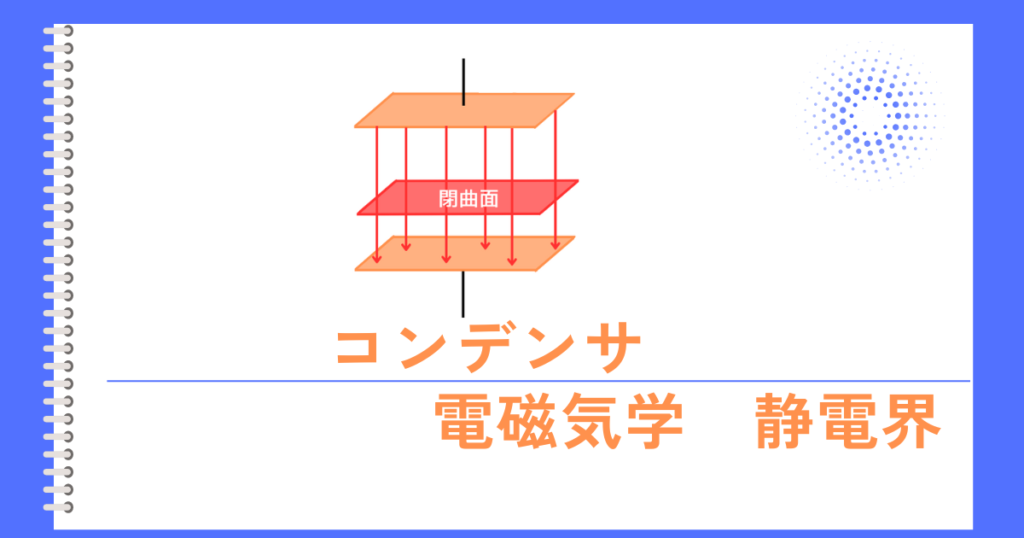
点電荷からの電気力線の広がりは、3次元的に全方面に放射状に広がりますので、閉曲面Sは、球状となります。
したがって、\(\oint_S dS=S\)で表される閉曲面の面積は、球の表面積となります。
球の表面積は、\(S=4πr^2\)なので、
\(\displaystyle E=\frac{Q}{ε_0S}\)
→ \(\displaystyle E=\frac{Q}{4πε_0r^2}\)
となります。
電束\(Q\)と電気力線の本数\(N\)[本]
\(Q[C]\)の電荷から出る電束は、\(Q[C]\)です。
つまり、電荷量=電束です。
\(Q[C]\)の電荷から出る電気力線の本数N[本]は、\(\displaystyle N=\frac{Q}{ε_0}\)です。
\(Q[C]\)の電束の密度は、電束密度\(D[C/m^2]\)です。
\(N\)[本]の電気力線の密度は、電界強度\(E[V/m]\)です。
電束\(Q[C]\)の広がりと、\(N\)[本]の電気力線の広がりのイメージ
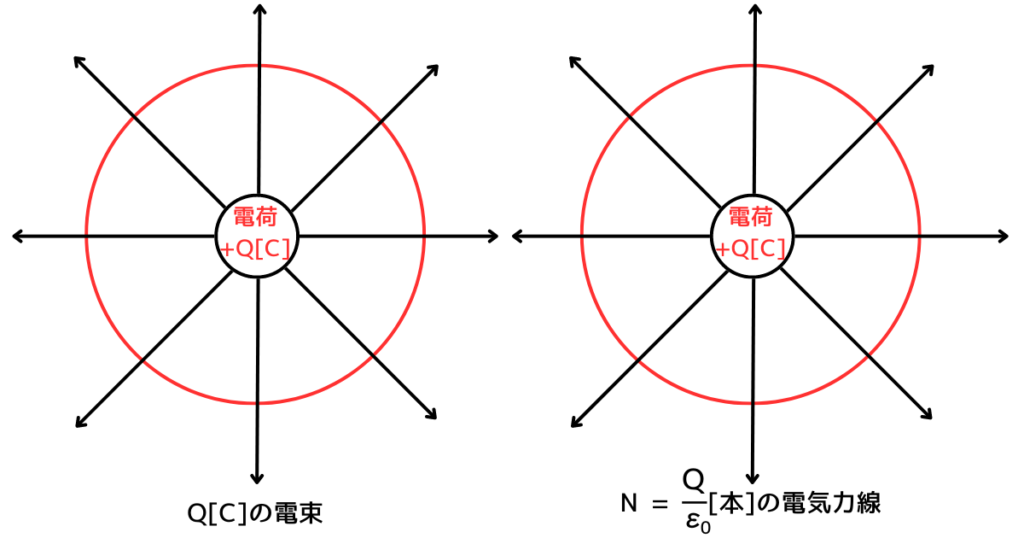
電束も、電気力線も、電荷から放射状に広がります。
電気力線の本数N[本]の式の意味
\(\displaystyle N=\frac{Q}{ε_0}\) …①
この①式は、便宜的に決めた式であり、①式自体に深い意味はありません。
では、便宜的とは何か。それは、ガウスの法則の式において、
\(\displaystyle \oint_S EdS=\frac{Q}{ε_0}\) …②
②式の右辺に便宜的に決めた①式を代入すると、次のように簡略化できるためです。
\(\displaystyle \oint_S EdS=N\) …③
次に、積分の形だとわずらわしいので、
\(\oint_S EdS=ES\)
と展開すると、③式は次のように変形できます。
\(ES=N\) ⇒ \(\displaystyle E=\frac{N}{S}\)
この式から、電界強度\(E[V/m]\)は、電気力線の本数\(N\)[本]の密度であると言えます。
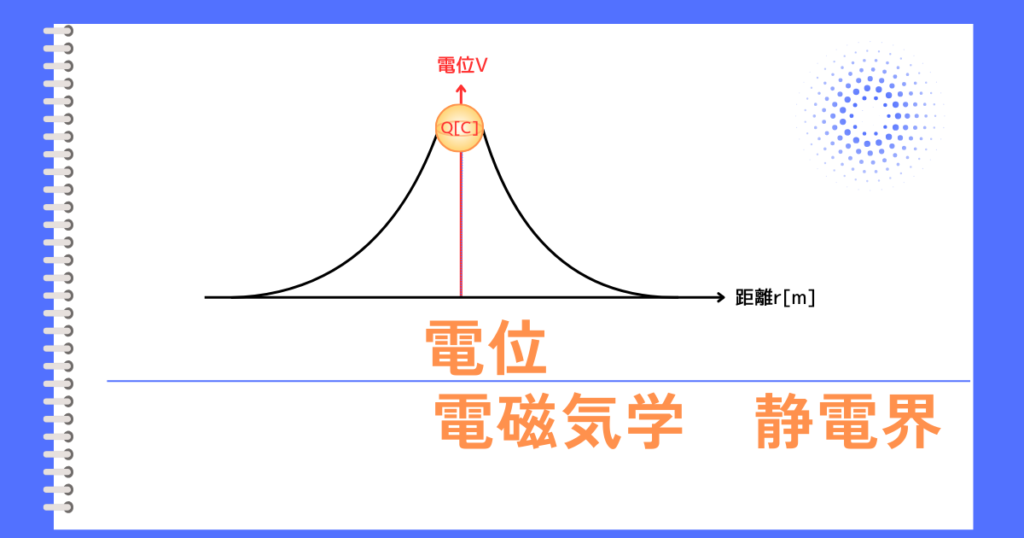
電位\(V[V]\)
点電荷\(Q[C]\)が作り出す電界中の電位は、次式で表すことができます。
\(\displaystyle V=\frac{Q}{4πε_0r}\)
電位の式について導出します。
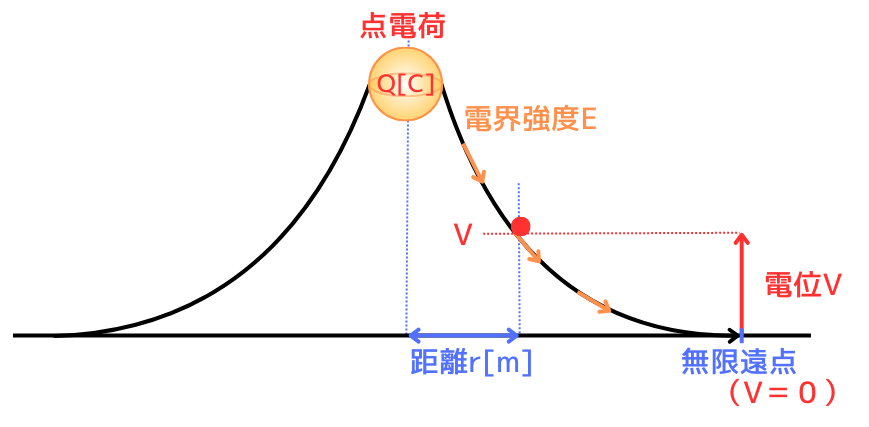
点電荷の作る電界の電界強度\(E[V/m]\)は、ガウスの法則から、
\(\displaystyle E=\frac{Q}{4πε_0r^2}[V/m]\) …①
この電界中で、単位電荷\(1[C]\)を基点から対象点まで移動させたときの電位を求めます。
このとき、
・基 点:無限遠点(∞)
・対象点:距離\(r[m]\)
とします。
電位\(V[V]\)と電界\(E[V/m]\)の関係式に①式を代入すると、
\(\displaystyle \begin{eqnarray}
V&=&-\int_{基点}^{対象点}E dr = -\int_{∞}^{r}\frac{Q}{4πε_0r^2} dr = \frac{Q}{4πε_0}\left[ \frac{1}{r} \right]_∞^r \\
&=& \frac{Q}{4πε_0}\left( \frac{1}{r}-\frac{1}{∞}\right) = \frac{Q}{4πε_0r}
\end{eqnarray}\)
以上、\(\displaystyle V=\frac{Q}{4πε_0r}\)が導出できました。
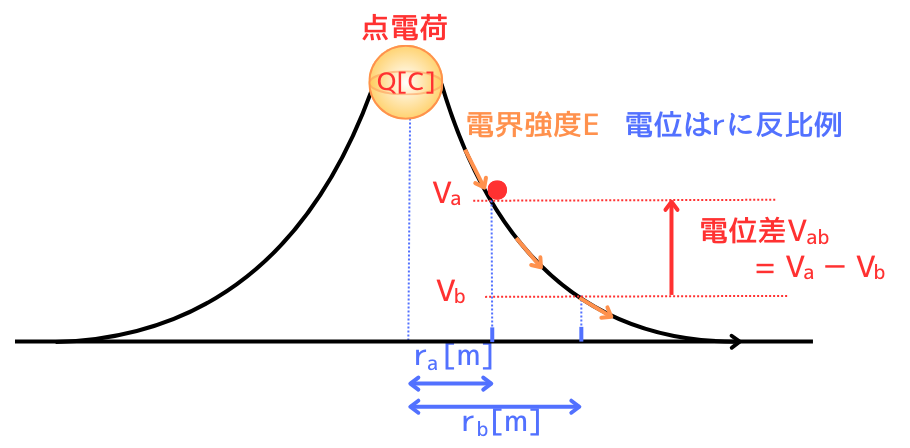
補足:電位差の導出
基点を無限遠点とせず、
・基 点:\(r_b[m]\)のとき、\(V_b[V]\)
・対象点:\(r_a[m]\)のとき、\(V_a[V]\)
とした場合、電位差\(V_{ab}=V_a-V_b\)になることついて導出します。
\(\displaystyle \begin{eqnarray}
V&=&-\int_{基点}^{対象点}E dr = -\int_{r_b}^{r_a} \frac{Q}{4πε_0r^2} dr = \frac{Q}{4πε_0}\left[ \frac{1}{r} \right]_{r_b}^{r_a} \\
&=& \frac{Q}{4πε_0}\left( \frac{1}{r_a}-\frac{1}{r_b}\right) = \frac{Q}{4πε_0r_a}-\frac{Q}{4πε_0r_b} = V_a-V_b
\end{eqnarray}\)
以上より、電位差\(V_{ab}=V_a-V_b\)が導出できました。
電束密度\(D[C/m^2]\)
電束密度D のガウスの法則
コンデンサの電束密度\(D[C/m^2]\)は
\(\displaystyle D=\frac{Q}{4πr^2}\)
点電荷の電束密度\(D[C/m^2]\)の式の証明

ガウスの法則の式を示します。
\(\oint_S DdS=Q\)
点電荷からの電気力線の広がりは、3次元的に全方面に放射状に広がりますので、閉曲面Sは、球状となります。
したがって、\(\oint_S dS=S\)で表される閉曲面の面積は、球の表面積となります。
球の表面積は、\(S=4πr^2\)なので、
\(\displaystyle D=\frac{Q}{S}\)
→ \(\displaystyle D=\frac{Q}{4πr^2}\)
となります。
電束密度\(D[C/m^2]\)と、電界強度\(E[V/m]\)
電束密度\(D[C/m^2]\)と、電界強度\(E[V/m]\)の関係は、
\(D=ε_0E\)
電束密度が必要な理由
電験三種の受験では試験範囲から外れる内容ですので、興味本位程度に読んでいただければ十分です。
結論から言うと、電束は誘電体中でも、真空中でも、誘電分極の影響を気にすることなく扱うことができるというメリットがあります。
誘電体に電荷が溜まると、電荷から発せられる電界によって電気双極子が整列する誘電分極という現象が発生します。
誘電分極が発生すると、電気力線を妨げる分極ベクトルが発生します。
このことにより、真電荷から出てきた\(\displaystyle \frac{Q}{ε}\)[本]の電気力線が誘電体を通ると不連続になります。
それに対し、電束密度は\(Q[C]\)で表される通り、誘電率に影響されないため、誘電体を通っても連続です。すなわち、誘電体の存在を無視することができます。
誘電体を通る電束密度と、電界強度の関係は、分極ベクトルを\(\boldsymbol{P}\)とすると、
\(\boldsymbol{D}=ε_0\boldsymbol{E}+\boldsymbol{P}\)
と表されます。
過去問
難易度 ★☆☆☆☆
| 電験三種 令和3年度 問2 | 誘電率によるクーロン力の変化の計算 |
難易度 ★★☆☆☆
| 電験三種 令和元年度 問1 | 点電荷の作る電界内の電位差の計算 |
| 電験三種 令和4年度上期 問2 | 3つの点電荷間に働くクーロン力のベクトル計算 |
難易度 ★★★★☆
| 電験三種 令和5年度下期 問2 | 導体球にかかるクーロン力の計算 |
関連記事(静電界に関する解説)
参考書
単位が取れる電磁気学シリーズは、電磁気学に関して根本的に理解を深めたい人に最もお勧めな参考書です。電磁気学で詰まりやすい大学生のバイブル的な一冊で、体系的な理解をすることができます。
電磁気ノートは、電験三種に必要な内容から、電験一種の内容まで全て入っています。
全て読破しようとすると、学習すべき範囲に対して過剰になるので、過去問のわからない箇所があったら、単位が取れる電磁気ノートで調べるという使用方法がお勧め。
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント