概要
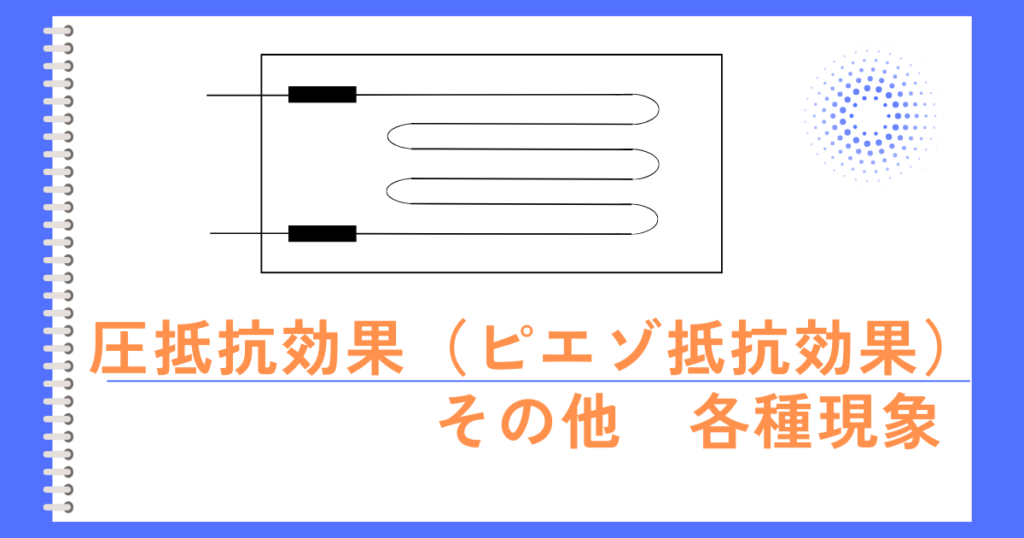
圧抵抗効果(ピエゾ抵抗効果)は、金属や半導体に力を加えて変形させると抵抗値が変化する現象です。
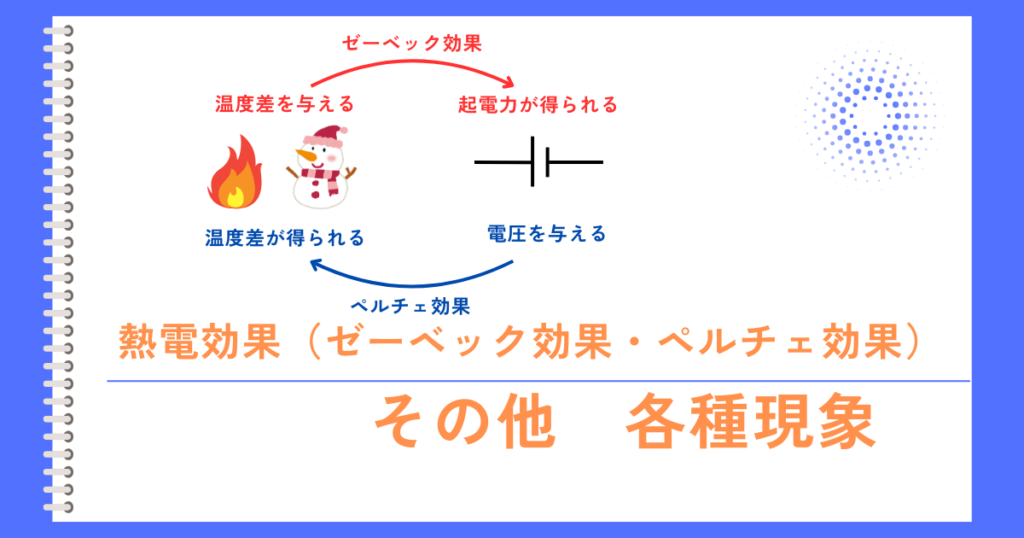
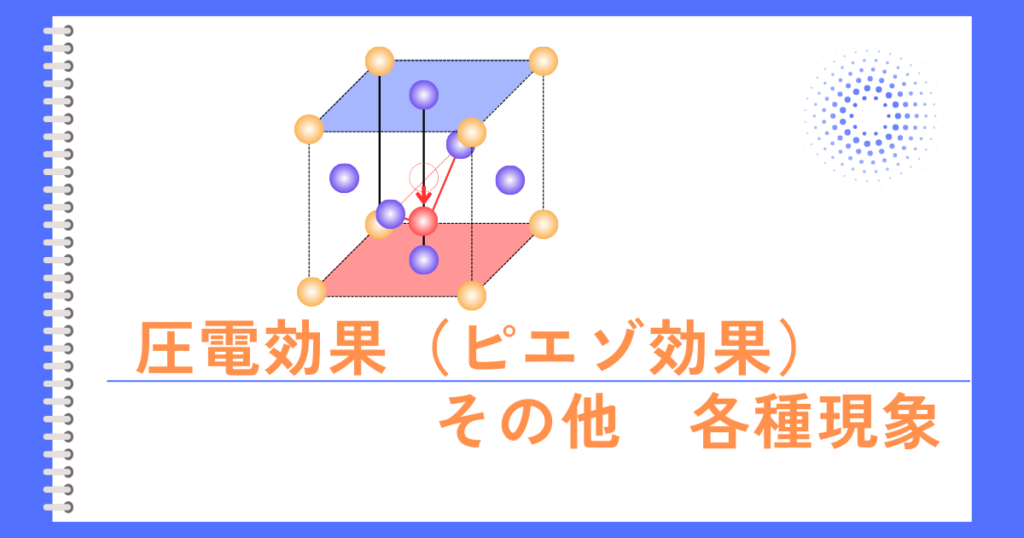
似た名称の現象に、圧電効果(ピエゾ効果)がありますが異なる現象です。
ピエゾ抵抗効果:圧力を加えると抵抗が変化
ピエゾ効果:圧力を加えると電圧が発生
※ピエゾ(piezo)とは、圧力を意味する言葉です。
応用例
加速度センサ・圧力センサ
ひずみゲージ(ストレインゲージ) ⇒ 体重計など
ひずみゲージの原理
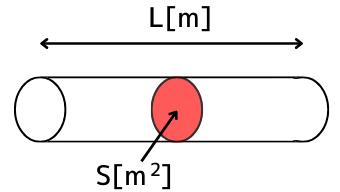
引っ張る
➡
抵抗率\(ρ[Ω・m]\)、抵抗の長さ\(L[m]\)、断面積\(S[m^2]\)の抵抗\(R[Ω]\)があるとします。
力が加えられていないときの抵抗値\(R[Ω]\)は、
\(\displaystyle R=ρ\frac{L}{S}\)
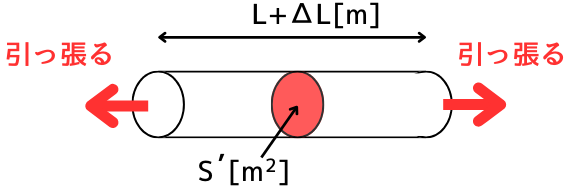
抵抗の両端が引っ張られ、抵抗の長さが\(L+ΔL[m]\)、断面積が\(S'[m^2]\)になったとします。
引っ張られて変形すると抵抗の断面積は細くなるので、断面積 \(S'<S\) です。
このときの抵抗値\(R'[Ω]\)は、
\(\displaystyle R’=ρ\frac{L+ΔL}{S’}\)
以上より、\(R’>R\)となります。
このように力を加えられることで、抵抗値が変化します。
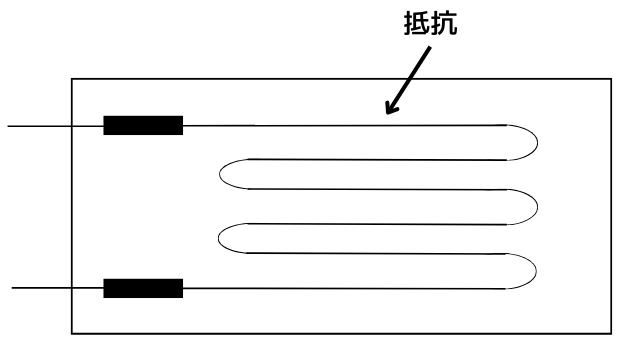
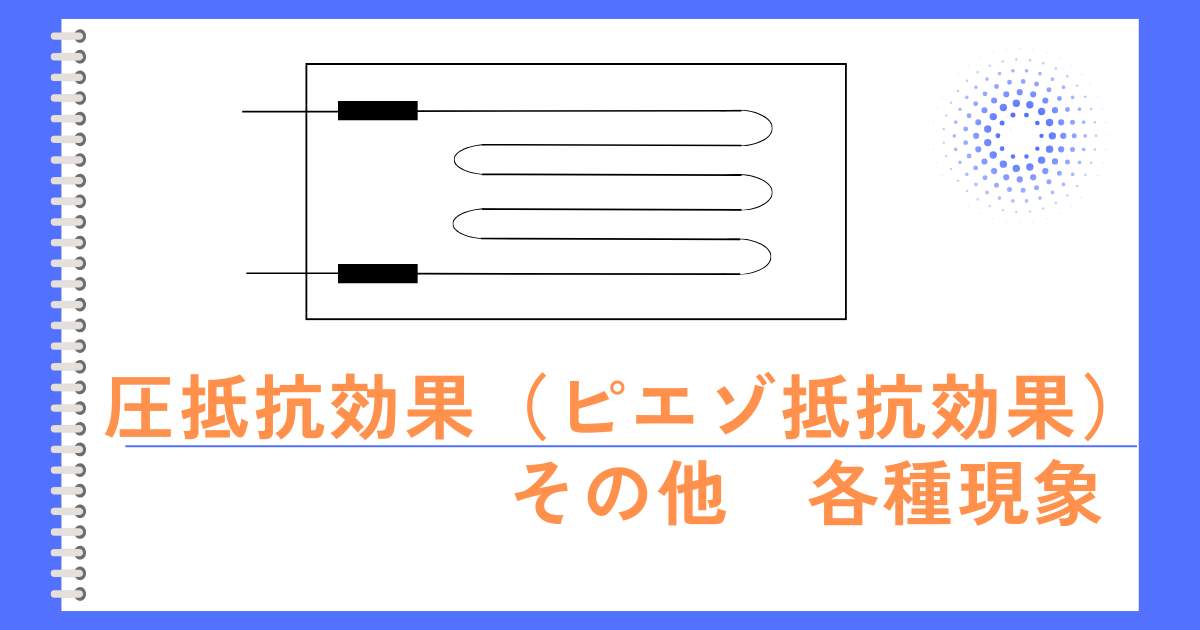
ひずみを得やすいように、抵抗は左図のように何回か折り返すような形で抵抗が配置されたものを使います。
ひずみゲージの測定回路
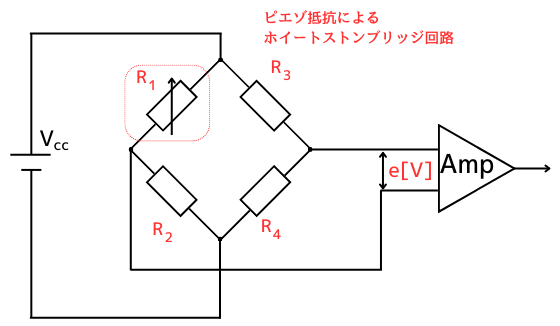
ピエゾ抵抗を歪ませたときの抵抗値変化\(ΔR[Ω]\)は非常に小さいです。
そのため、ピエゾ抵抗を使ってひずみゲージを作るには、ホイートストンブリッジ回路を使って精密な測定をする必要があります。
図のように、ホイートストンブリッジ回路の構成を、ピエゾ抵抗\(R_1[Ω]\)と、抵抗\(R_2[Ω]\)、\(R_3[Ω]\)、\(R_4[Ω]\)で組んだとします。
この時、アンプに印加される測定電圧\(e[V]\)は、次式で表されます。
\(\displaystyle e=\frac{R_1R_4-R_2R_3}{(R_1+R_2)(R_3+R_4)}V_{cc}\)
圧力が加えられておらず、歪みがないとき、
\(R_1=R_2=R_3=R_4=R\)
とすると、\(e=0[V]\)となります。
圧力が加えられて、ピエゾ抵抗の抵抗値が\(R_1=R+ΔR\)と変化したとき、
\(R_2=R_3=R_4=R\)とすると、
\(\displaystyle e=\frac{R(R+ΔR)-R^2}{2R(2R+ΔR)}V_{cc}\)
⇔ \(\displaystyle e=\frac{ΔR}{4R+2ΔR}V_{cc}\)
ここで、\(R>>ΔR\)なので、
\(4R+2ΔR≒4R\)と近似します。
\(\displaystyle e=\frac{ΔR}{4R}V_{cc}\)
電圧\(e[V]\)が求められたので、信号増幅すると歪みによる抵抗値の変化を読み取ることができます。
次に、\(ΔR/R\)と、ひずみ量\(ε\)の関係の係数を\(K\)とすると、次式で表せます。
\(\displaystyle \frac{ΔR}{R}=Kε\)
\(\displaystyle e=\frac{V_{cc}}{4}Kε\)
⇔ \(\displaystyle ε=\frac{4}{KV_{cc}}e\)
以上より、ひずみ量\(ε\)を求めることが出来ました。
関連記事(その他)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント