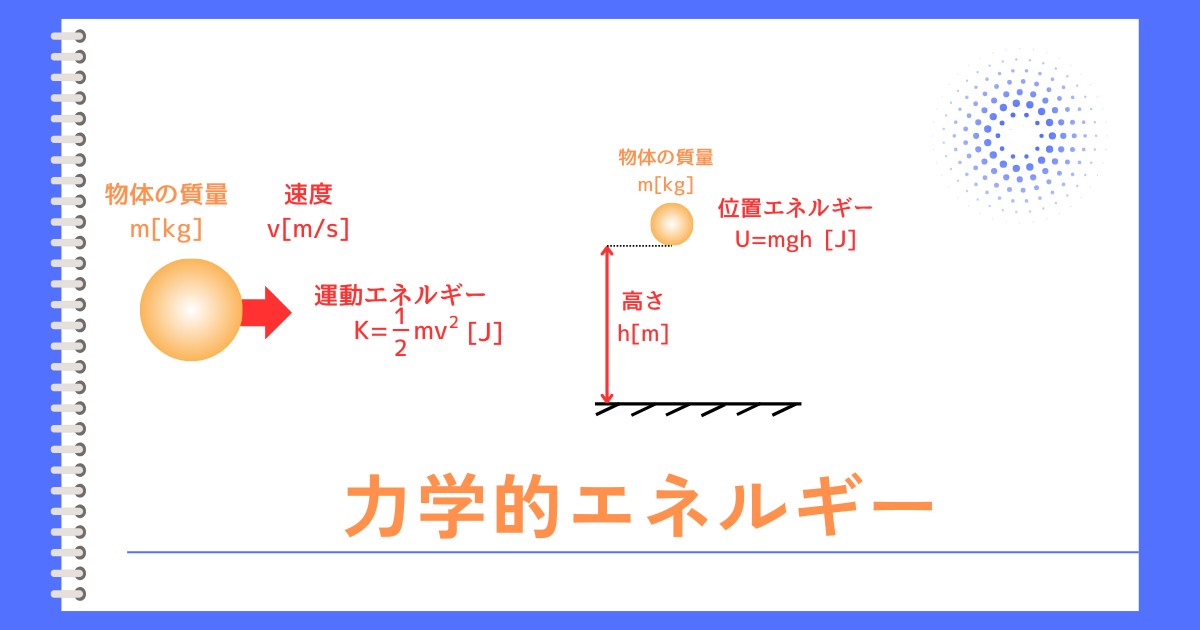
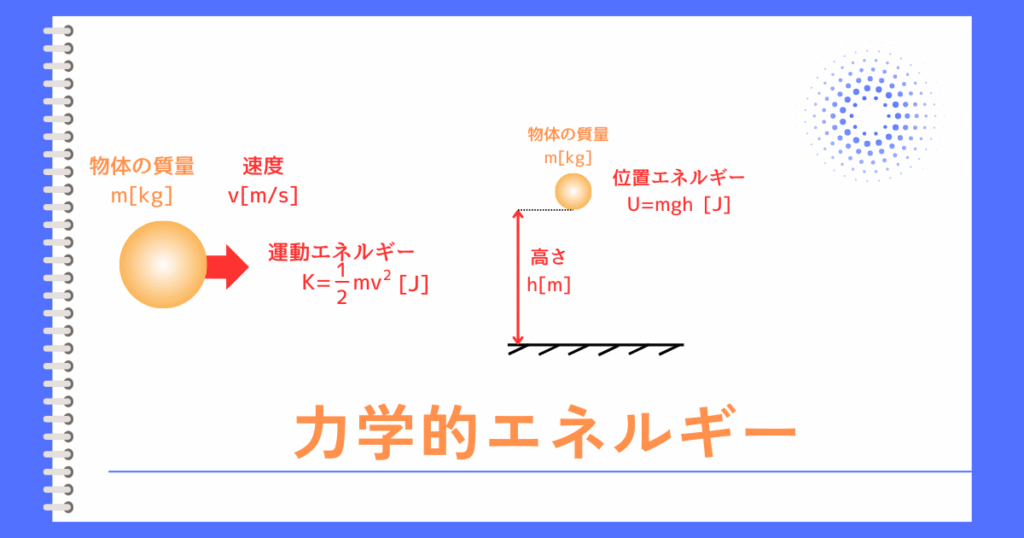
力学的エネルギー
力学的エネルギーとは、運動エネルギーと、位置エネルギーを足し合わせたものです。
運動エネルギー、位置エネルギーと、エネルギー保存の法則について解説します。
仕事
仕事\(W[J]\)の定義は、物体に力\(F\)を加えたとき、加えられた力の方向に物体が\(x_0\)から\(x_1\)に移動した際に、その力によって行われたエネルギーの伝達量です。つまり、仕事の定義式は次式となります。
仕事の定義式
\(\displaystyle W=\int_{x_0}^{x_1}Fdx\)
運動エネルギー
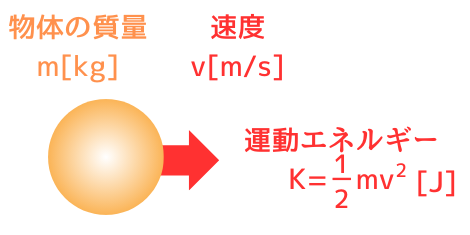
運動エネルギーの公式
\(\displaystyle K=\frac{1}{2}mv^2\)
運動エネルギーは、ある速度で動いている物体が持っているエネルギーです。
他の物体に当たると、運動エネルギーが伝わることでその物体を動かすことが出来ます。
同じ速度で飛んでくるピンポン玉よりも、野球ボールの方が受け取る際に衝撃が強いです。
同じ野球ボールでも、キャッチボールで肩慣らし程度に投げる速度の球よりも、野球ピッチャーが本気で投げる速度の球の方が衝撃が強いです。
つまり、運動エネルギーは質量\(m[kg]\)が重い程、速度\(v[m/s]\)が速い程、エネルギーが大きくなります。
運動エネルギーの導出
仕事\(W\)の定義式は、次式です。
\(\displaystyle W=\int_{x_0}^{x_1}Fdx\)
\(x_0=0\)、\(x_1=x\)として、次のように書き変えます。
\(\displaystyle W=\int_{0}^{x}Fdx\) …①
力\(F\)は、質量\(m\)、加速度\(a\)を使い、運動方程式から次式で表されます。
\(F=ma\) …②
加速度\(a\)は、速度\(v\)の時間に対する変化の割合なので、
\(\displaystyle a=\frac{dv}{dt}\) …③
①式に②・③式を代入すると、
\(\displaystyle \begin{eqnarray}
W&=&\int_{0}^{x}Fdx=\int_{0}^{x}madx=\int_{0}^{x}m\frac{dv}{dt}dx \\ \\
&=&\int_{0}^{v}m\frac{dx}{dt}dv=\int_{0}^{v}mvdv=\left[ \frac{1}{2}mv^2 \right]_{0}^{v}=\frac{1}{2}mv^2
\end{eqnarray}\)
位置エネルギー

位置運動エネルギーの公式
\(U=mgh\)
位置エネルギーはポテンシャルエネルギーとも呼ばれます。
位置エネルギーは、物体の高さや、ばねの伸び等の位置によって、物体に蓄えられるエネルギーです。
物質が高い位置にあることで、自由落下による仕事をする能力を持ちます。
位置エネルギーの導出
仕事\(W\)の定義式は、次式です。
\(\displaystyle W=\int_{0}^{h}Fdy\) …①
力\(F\)は、質量\(m\)、重力加速度\(g\)を使い、運動方程式から次式で表されます。
\(F=mg\) …②
重力加速度\(g\)は、常に一定です。
①式に②・③式を代入すると、
\(\displaystyle \begin{eqnarray}
W&=&\int_{0}^{h}Fdy=\int_{0}^{h}mgdy \\ \\
&=&\left[ mgy \right]_{0}^{h}=mgh
\end{eqnarray}\)
エネルギー保存の法則
エネルギー保存の法則
\(\displaystyle \frac{1}{2}mv^2+mgh=\)一定
物体の位置エネルギーと運動エネルギーの和は一定に保たれるという法則です。
上記の式は、重力に対するエネルギー保存の法則です。
流体のエネルギーを考えるときは、運動エネルギー、位置エネルギーに加え、圧力エネルギーもあります。この3つのエネルギーが一定である法則はベルヌーイの定理と呼ばれます。
電力科目の水力発電の単元における重要な定理です。
エネルギー保存の法則を拡張して考えると、熱、電気エネルギー等も含め、エネルギーの形態の変化の前後は常に一定に保たれます。
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント