概要
デジタル回路は、入出力信号が高いときに1、低いときに0と表現され、1・0の組合せで機能を実現する電子回路です。
デジタル回路は、論理回路を組み合わせることで作られ、NAND・AND・OR・NOR・XOR・NOTの6つの基本要素回路で構成されます。
全ての基本要素回路は、NAND回路で表現することができることから、NAND回路が最も重要な回路です。NAND回路で構成されるフラッシュメモリがあるように、この特性は実用的な論理回路を学ぶ上では重要です。
各論理回路の要素を表すための記号をシンボル。論理回路が入力信号に対して、どのような出力をするかを表にしたものを真理値表。真理値表を式で表したものを論理式と呼びます。
本頁では、各回路のシンボル、論理式、NAND等価回路と、真理値表について示していきます。
なお、電験の勉強をするだけの場合は、NAND等価回路は特に覚える必要性はないです。
基本要素回路
NAND
Not ANDでNAND回路です。NAND回路は基本要素回路の中でも最も重要な回路です。
①NAND回路で、他の基本要素回路を全て表現できる。
NOT・AND・OR等の他の素子を置いてデジタル回路を構成すると、回路の使用状況によって過不足が出ますが、NANDだけで構成すれば回路の過不足が発生しません。
②トランジスタの使用個数が少ない。
PMOS2つ、NMOS2つでNAND回路を構成することができます。
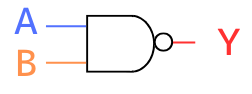
シンボル
論理式
\(Y=\overline{A・B}\)
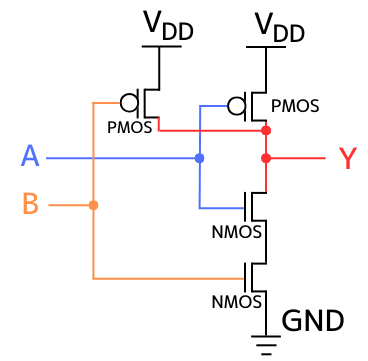
内部回路図
真理値表
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
AND
AND回路は、論理積とも呼ばれ、2つの入力が両方とも1の時のみ出力が1となる回路です。
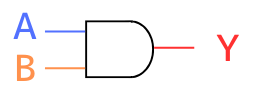
シンボル
論理式
\(Y=\overline{A・B}\)
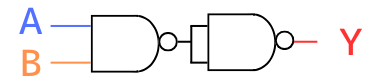
NAND等価回路
真理値表
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
OR
OR回路は、論理和とも呼ばれ、2つの入力のいずれかが1のときに出力が1となる回路です。
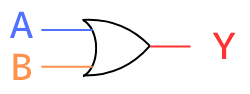
シンボル
論理式
\(Y=A+B\)
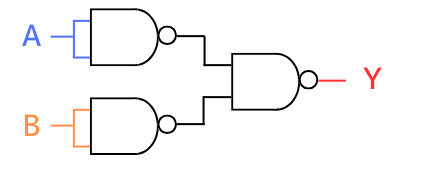
NAND等価回路
真理値表
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
NOR
Not ORでNOR回路です。
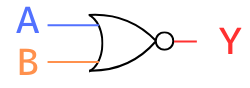
シンボル
論理式
\(Y=\overline{A+B}\)
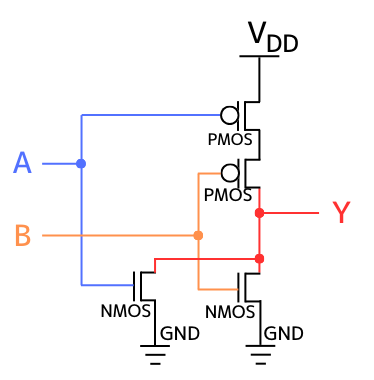
内部回路図
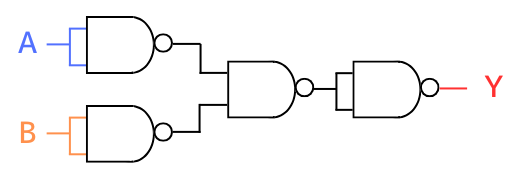
NAND等価回路
真理値表
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
XOR
XOR回路は、排他的論理和と呼ばれ、2つの入力のどちらかが1で、もう片方は0のときに出力が1となる回路です。
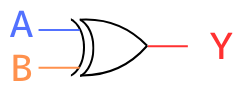
シンボル
論理式
\(Y=A\overline{B}+\overline{A}B\)
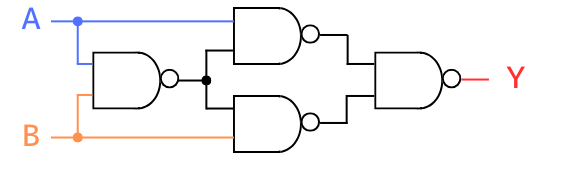
NAND等価回路
真理値表
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOT
NOT回路は、インバータや反転回路とも呼ばれ、入力の逆が出力される回路です。
入力が1である場合0が出力され、0が入力されると1が出力されます。
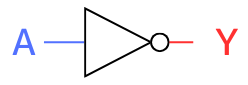
シンボル
論理式
\(Y=\overline{A}\)
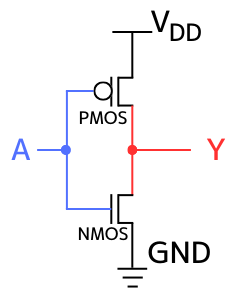
内部回路図
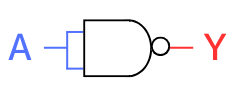
NAND等価回路
真理値表
| A | Y |
| 0 | 1 |
| 1 | 1 |
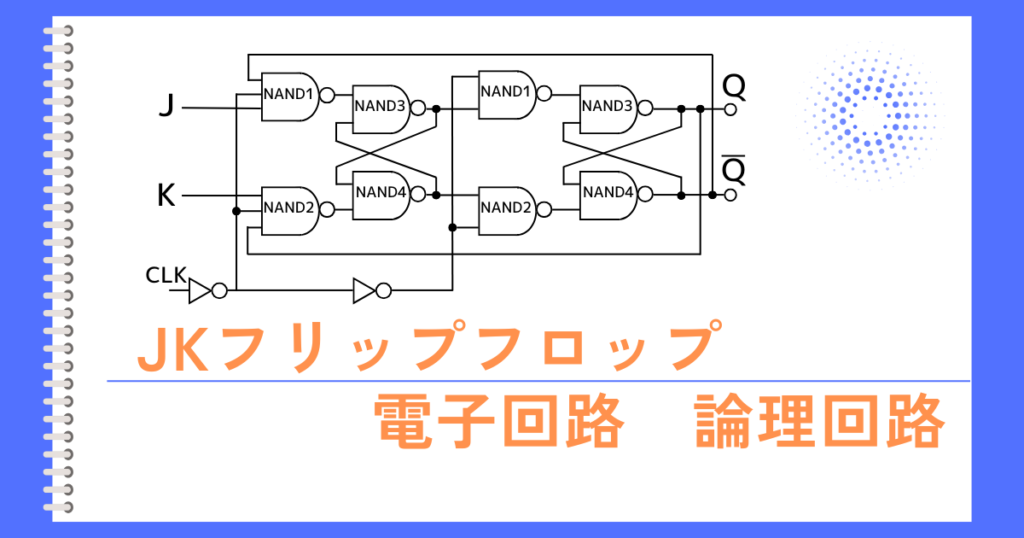
関連記事(その他)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。
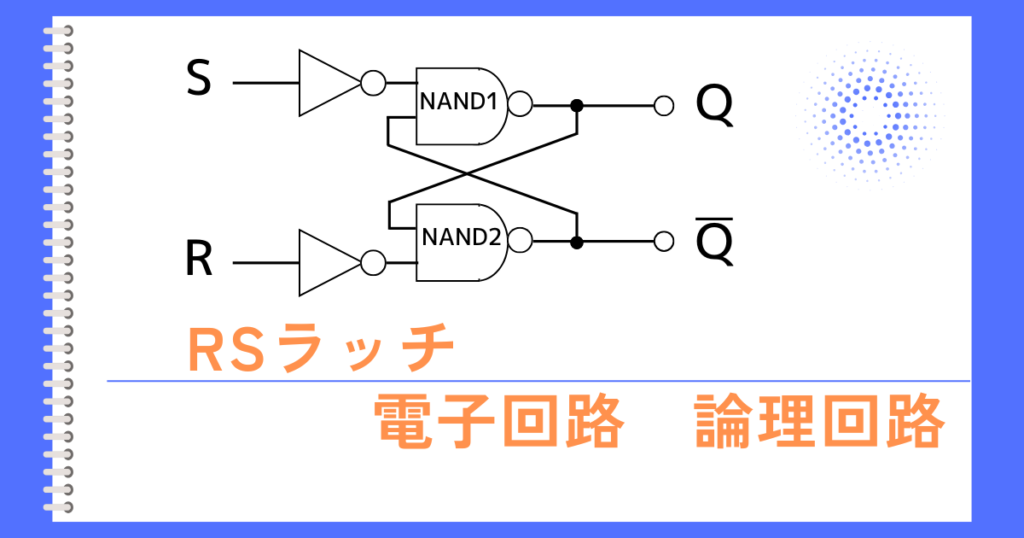
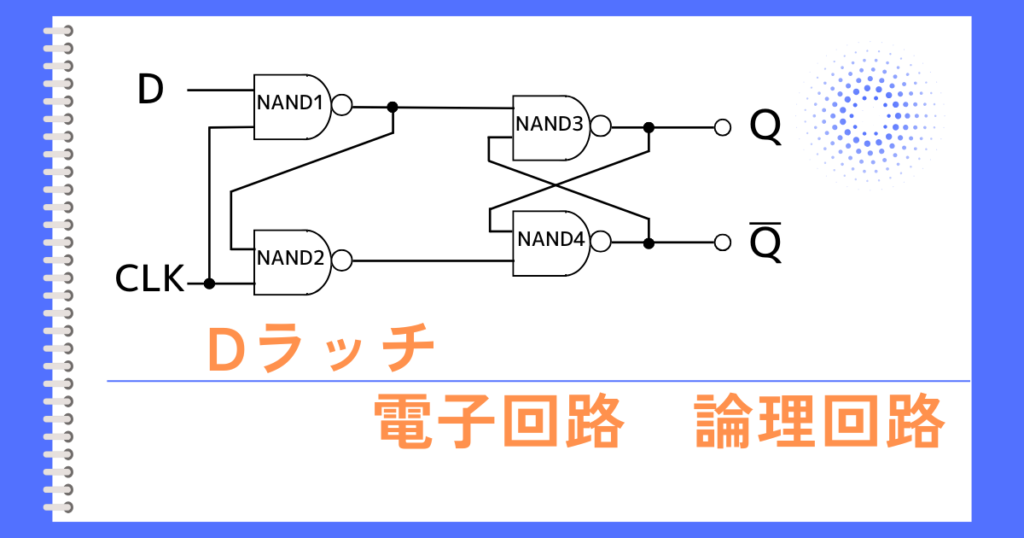
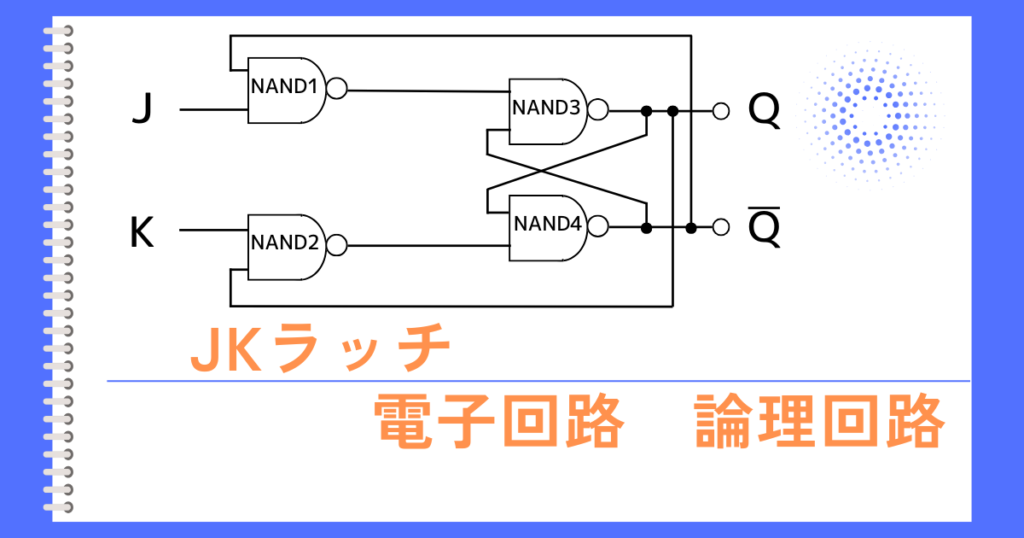
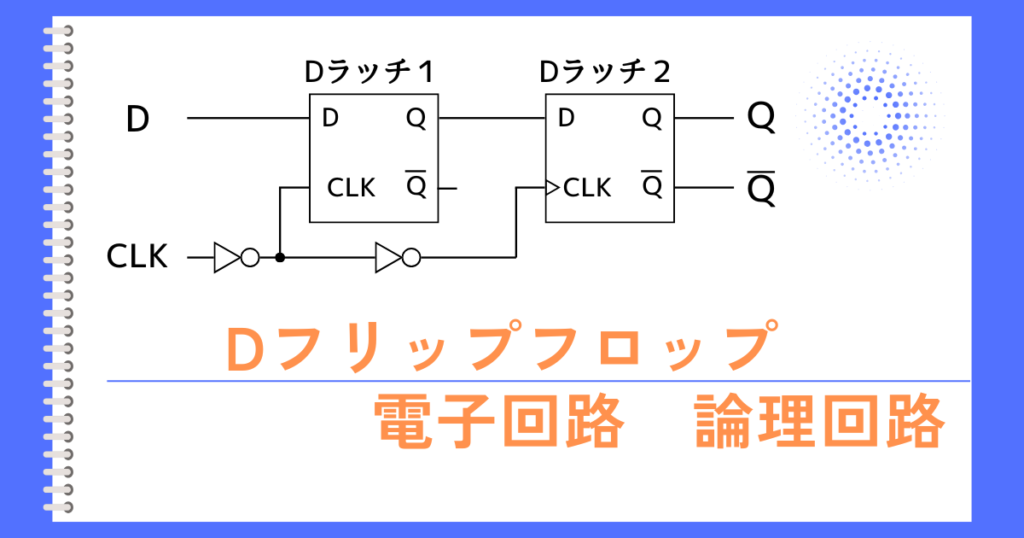

コメント