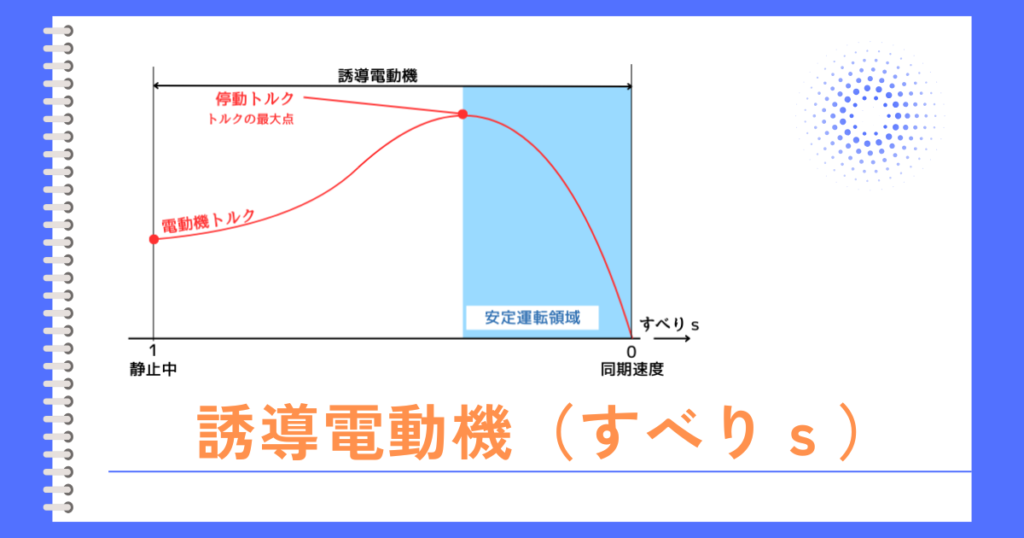
概要
誘導電動機の等価回路について解説していきます。
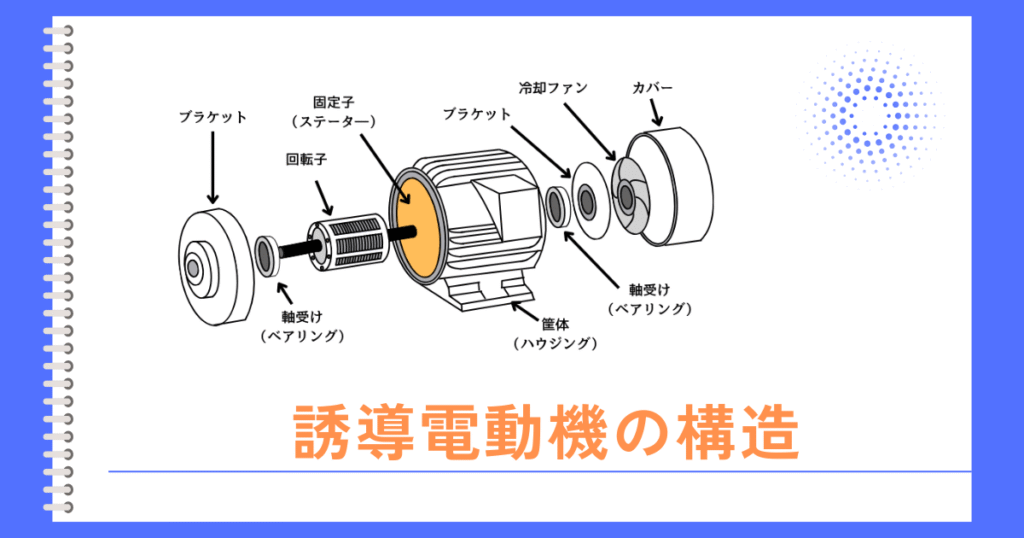
本頁では、誘導電動機の構造から、L形等価回路がどのように導出されるかを示します。
計算については、別途解説します。(➡L形等価回路の計算)
誘導電動機の等価回路図は、一見すると複雑な回路のように見えます。
しかし、その成り立ちについて理解をすれば、簡単に描けるようになります。
つまり、回路を描けるようになることが誘導電動機の理解に関する第一歩です。
そして、回路を描けるようになるためには、誘導電動機の構造が、どのように等価回路に落とし込まれ、計算しやすいように変換されていくかを理解していくことが重要です。
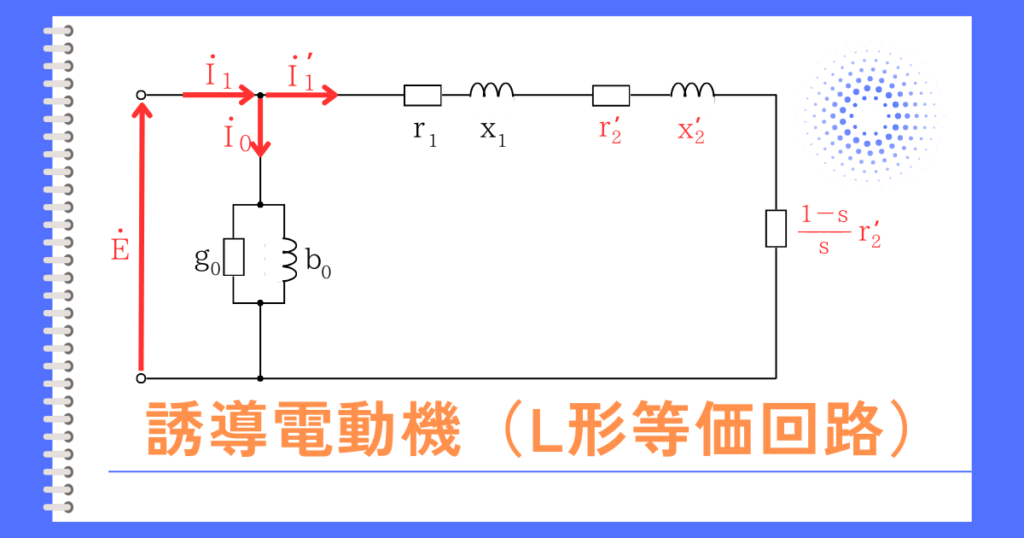
L形等価回路図
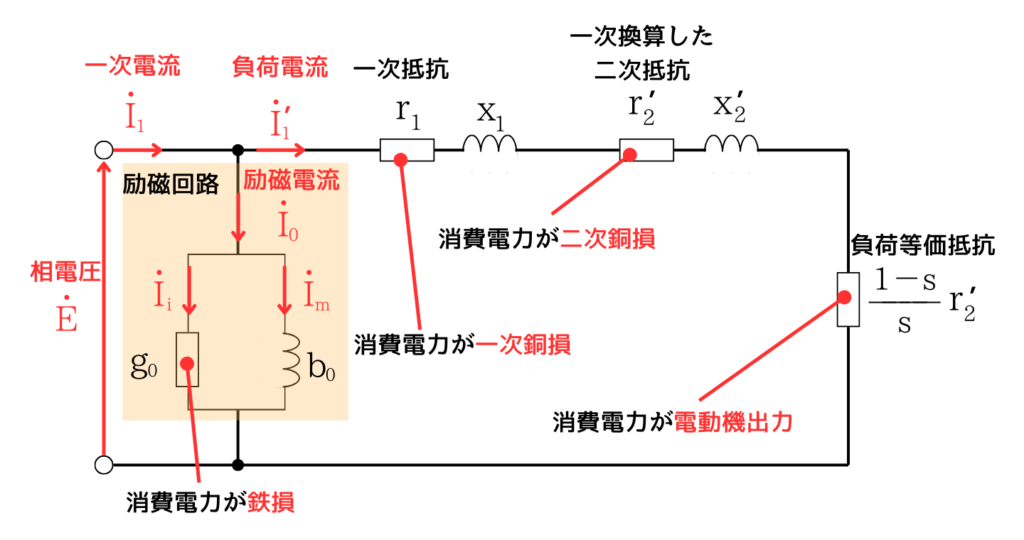
誘導電動機の電流
\(\dot{I_1}\):一次電流 電源から供給される電流
\(\dot{I_0}\):励磁電流 回転磁界を作る電流
\(\dot{I’_1}\):負荷電流 回転子に流れる電流を、一次側に換算した電流
励磁回路
\(g_0\):励磁コンダクタンス
\(b_0\):励磁サセプタンス
主回路
\(r_1\):一次抵抗
\(x_1\):一次リアクタンス
\(r’_2\):一次側換算した二次抵抗
\(x’_2\):一次側換算した二次リアクタンス
\(\frac{1-s}{s}r’_2\):負荷等価抵抗(一次側換算した機械出力)
L形等価回路の導出
誘導電動機の等価回路は、一次回路(固定子)と二次回路(回転子)が磁気結合するため、変圧器の等価回路と同じ回路で表されます。
ただし、二次回路(回転子)が回転するため、すべりの影響を、その等価回路に反映させる必要があります。
式の変形では、すべりの影響を無視できるようにしてから、変圧器と同様の処理をしたうえでL形等価回路を作成していきます。
誘導電動機の等価回路の導出をしていく工程一覧
1.等価回路の作成(一次側)
2.等価回路の作成(二次側)
3.等価回路の作成(一次・二次合体)
4.等価回路の変形(二次側の変形)
├ ①すべりの影響をなくす
├ ②二次銅損と機械出力を分別する
└ ③変圧比の影響をなくす
5.L形等価回路の作成
1.等価回路の作成(一次側)
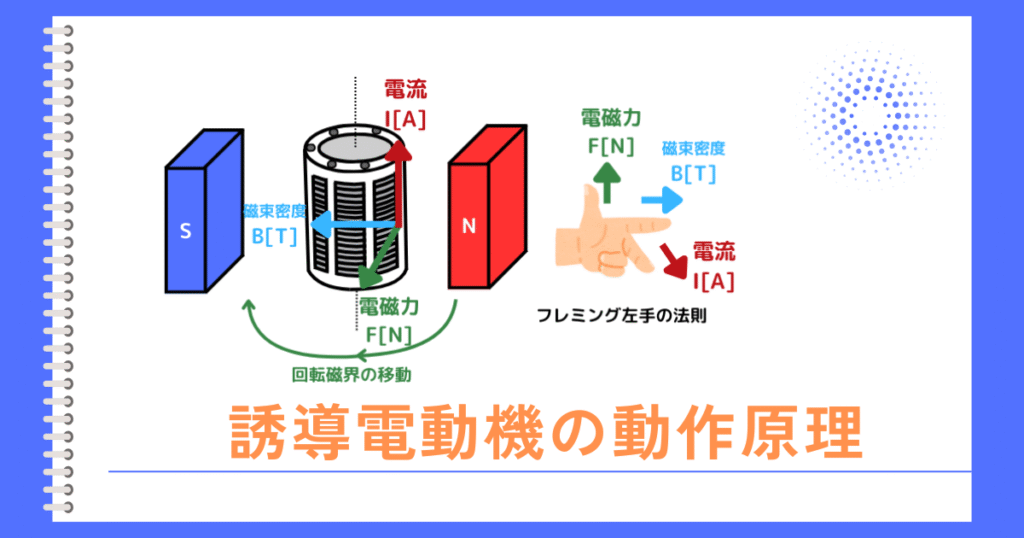
誘導電動機に三相電源を接続すると、一次巻線(固定子)に電流が流れ、誘導電動機内部に回転磁界を発生させます。これを励磁と呼びます。

左図は、筐体の内側に取り付けられている一次巻線(固定子)の断面に、一次抵抗\(r_1\)と、一次漏れリアクタンス\(x_1\)を描き込んだモデルです。

上図の断面のモデルから、一次巻線の回路を三相分まとめて等価回路に描き替えると左図になります。
励磁コンダクタンス\(g_0\)と、励磁サセプタンス\(b_0\)の回路は、無負荷損を表す励磁回路です。
励磁回路は、誘導電動機内部に回転磁界を発生させる回路です。
2.等価回路の作成(二次側)
二次巻線(回転子)は、導体棒からなるコイル辺が持つ二次抵抗\(r_2\)と、二次漏れリアクタンス\(sx_2\)で表すことができます。

2次側の抵抗成分\(r_2\)について
抵抗成分は周波数に影響されません。
そのため、すべりの変化の影響を受けないことから\(r_2\)です。
2次側のリアクタンス成分\(sx_2\)について
リアクタンスは\(X=2πfL\)の式で表せる通り、周波数に比例します。
そのため、\(sx_2\)となります。
3.等価回路の作成(一次・二次合体)
一次側回路の等価回路と、二次側回路の等価回路を組み合わせます。
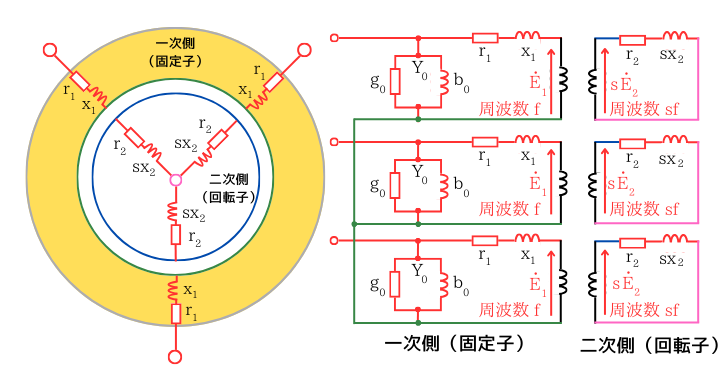
三相分の等価回路を描くのは面倒なので、一相分だけ取り出します。
この図は、変圧器の等価回路とほぼ同じ回路です。

周波数について
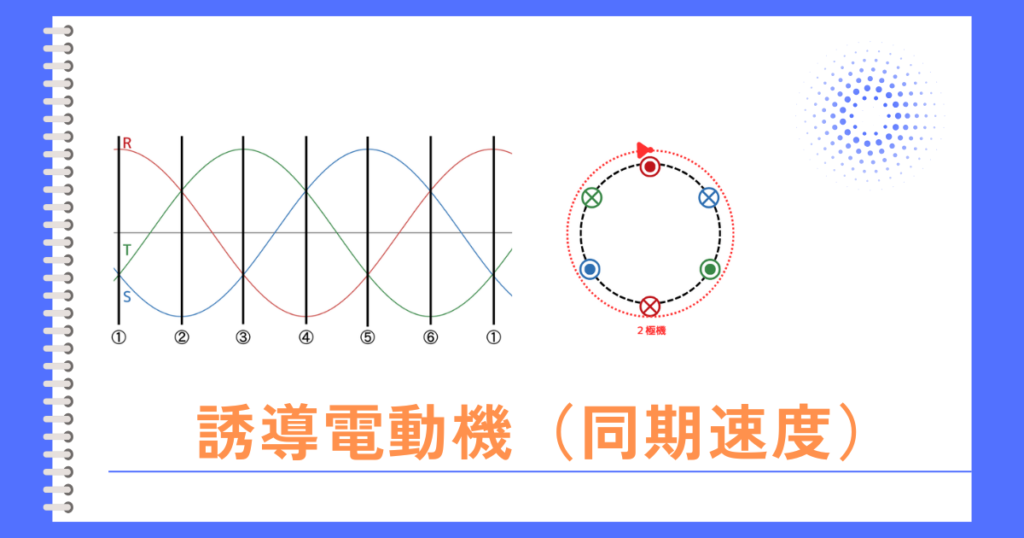
一次巻線の周波数\(f_1\)は、電源周波数\(f[Hz]\)です。
二次巻線の周波数\(f_2\)は\(f_2=sf[Hz]\)です。
二次周波数が\(f_2=sf[Hz]\)となる理由(すべり周波数)
二次巻線の周波数\(f_2\)は、回転磁界と回転子の相対速度(\(N_s-N\))によって決まります。
回転子がすべり\(s\)で回転しているときの相対速度は、すべりの定義式から\(N_s-N=sN_s\)となります。
そのため、二次巻線の周波数\(f_2\)は、一次巻線の周波数\(f\)の\(s\)倍である\(sf\)になります。
この二次巻線の周波数をすべり周波数と呼びます。
電圧について
変圧器の回路と同じなので、変圧比を\(a\)としたときの一次電圧\(\dot{E_1}\)と、二次電圧\(\dot{E_2}\)の関係は
\(\dot{E_1}=a\dot{E_2}\) です。
そして、二次電圧は、ファラデーの法則(\(v=-N \frac{dΦ}{dt}\))で表されるように、磁束変化の大きさと速さに比例する電圧です。
そのため、二次電圧は、磁束変化の速さである周波数に比例します。
二次周波数\(f_2\)がすべり\(s\)に比例することから、二次電圧もすべり\(s\)に比例します。
そのため、二次電圧は\(s\)倍をした\(s\dot{E_2}\)になります。
4.等価回路の変形(二次側の変形)
誘導機の回路のままでは計算しづらいです。
計算をしやすくするため、二次回路を変形していきます。
二次電圧\(\dot{E_2}\)を一次電圧\(\dot{E_1}\)と等しくなるように①~③の二次回路の変形をすることで、一次換算します。一次換算をすることで、二次回路を一次回路と一つながりの回路として取り扱うことができるようになります。
①すべりの影響をなくす
②二次銅損と機械出力を分別する
③変圧比の影響をなくす
①すべりの影響をなくす(二次側の変形)
すべりの変化によって、二次周波数、二次電圧が変動すると取り扱いづらいため、すべりの影響をなくしていきます。
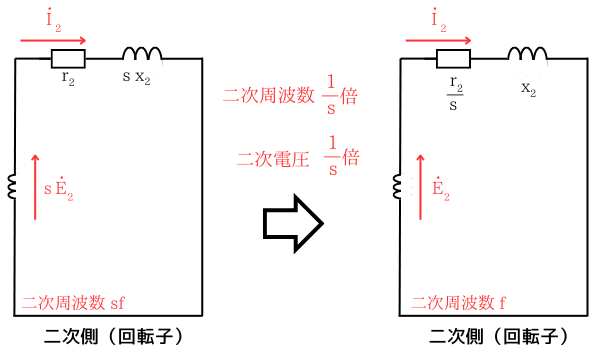
- 二次周波数\(f_2\)を\(\frac{1}{s}\)倍し、 \(sf\) ➡ \(f\) に変換。
- 二次電圧\(\dot{E_2}\)も、すべりに比例するので\(s\dot{E_2}\) ➡ \(\dot{E_2}\)。
- 二次電流\(\dot{I_2}\)は変化させたくないので、二次抵抗\(r_2\)と、二次リアクタンス\(x_2\)を\(\frac{1}{s}\)倍する。
②二次銅損と機械出力を分別する(二次側の変形)
二次抵抗\(\frac{r_2}{s}\)で消費される電力には、
・回転子巻線の銅損
・誘導電動機の機械出力
の2つが含まれています。
そのため、\(\frac{r_2}{s}\)を、本来の二次巻線抵抗である\(r_2\)と、機械出力の2つに分離することを考えます。
\(\frac{r_2}{s}-r_2=\frac{1-s}{s}r_2\)

\(r_2\)は、回転子巻線の銅損を表す抵抗です。
\(r_2\)で消費される電力は、ジュール熱になります。
\(\frac{1-s}{s}r_2\)は、誘導電動機の機械出力を表す抵抗です。これは、実際に\(\frac{1-s}{s}r_2\)の抵抗があるわけではなく、機械出力エネルギーを、抵抗のジュール熱とみなして計算するための等価抵抗です。
③変圧比の影響をなくす(二次側の変形)

一次側回路と、二次側回路は、変圧比\(a\)倍の変圧器と考えることができることから、
一次電圧\(\dot{E_1}\)と二次電圧\(\dot{E_2}\)の関係は、\(\dot{E_2}=\frac{1}{a}\dot{E_1}\)です。
一次電流\(\dot{I_1}\)と二次電流\(\dot{I_2}\)の関係は、\(\dot{I_2}=a\dot{I_1}\)です。
二次電圧を、\(\dot{E_2}\)➡\(\dot{E_1}\)となるように、二次抵抗、二次リアクタンスを等価変換します。
変圧器の等価回路と同じく、\(a^2\)倍することで等価変換できます。
そして、一次側の電圧に換算した二次側抵抗を\(r’_2\)、二次リアクタンスを\(x’_2\)とすると、
\(r’_2=a^2r_2\)、\(x’_2=a^2x_2\) です。
5.L形等価回路の作成
変形した二次側回路を、一次側回路と一緒に描きます。
一次電圧と二次電圧が同じで線間が同電位なので、一次回路と二次回路を一つにまとめることができます。まとめた回路を、L形等価回路と呼びます。
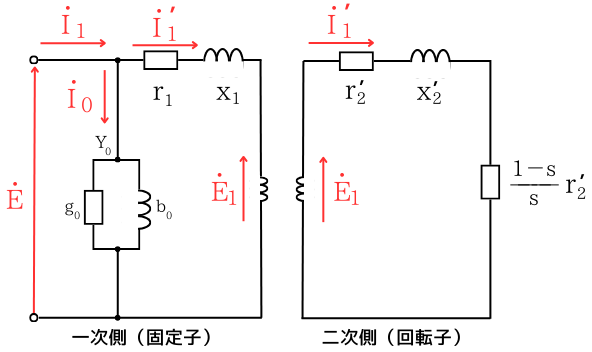
➡
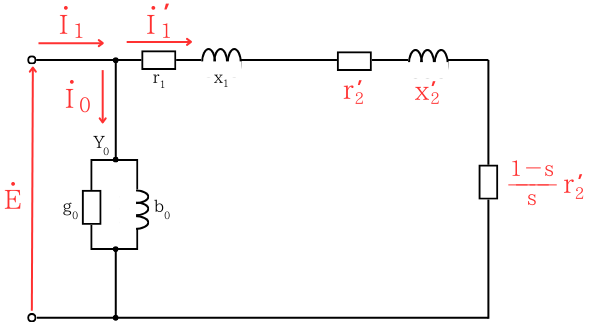
L形等価回路
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。






コメント