概要
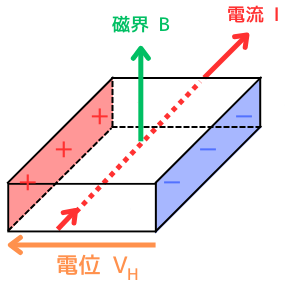
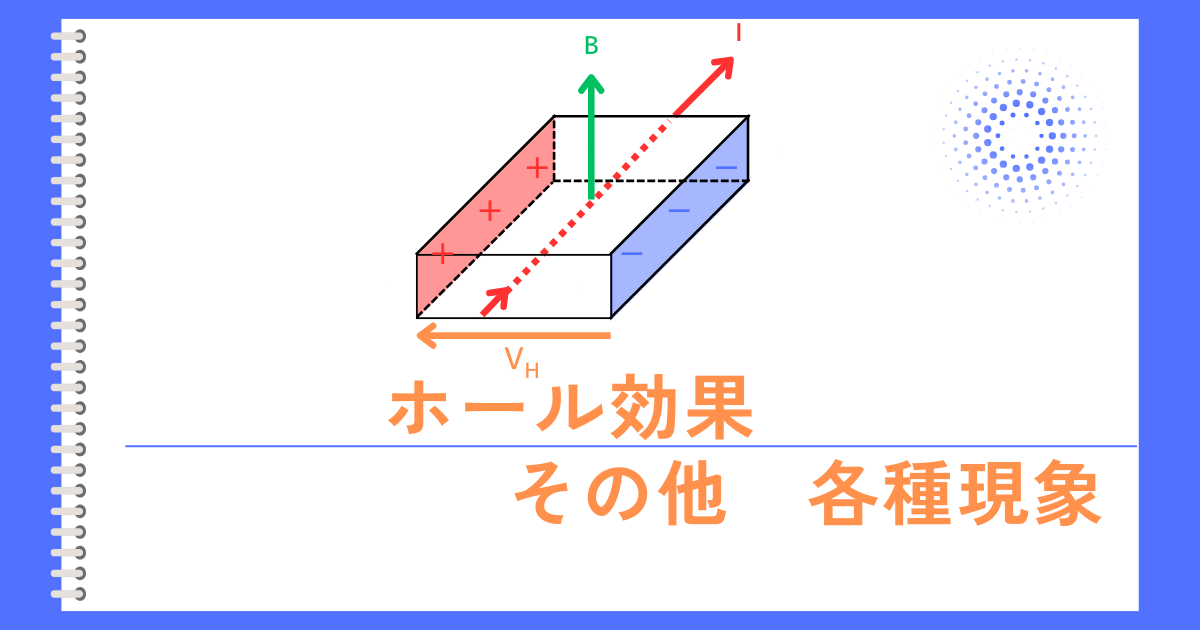
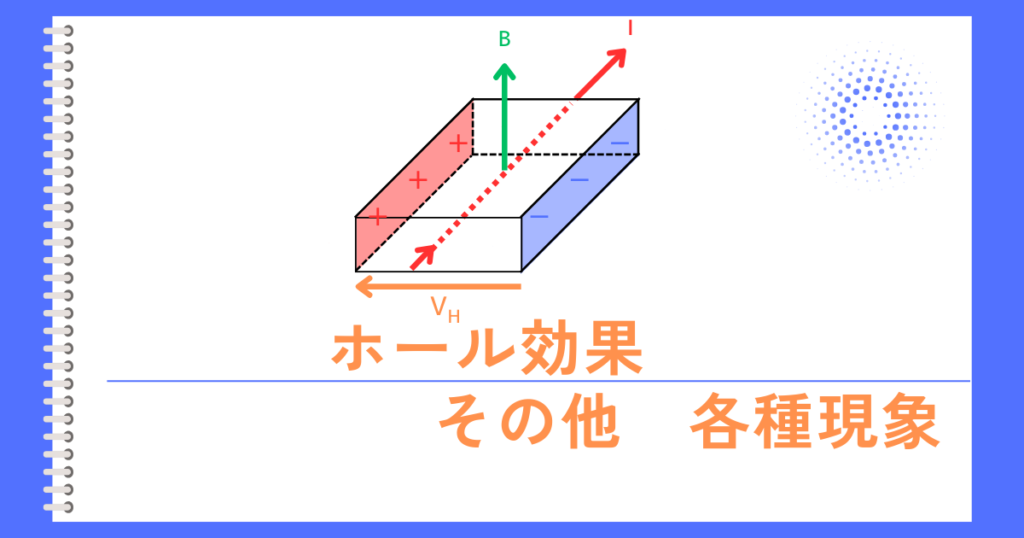
ホール効果は、電流\(I\) が流れている物質に磁界\(B\) を加えると、電流と磁界に垂直な方向に電位\(V_H\) が発生する現象です。
このホール効果を使うことで、ホールセンサを作ることが出来ます。
ホールセンサは、磁界の強さと向きを電圧の大きさと正負に変換する磁気センサです。
応用例
位置検出、開閉検出、方位検出等々、様々な応用が利きます。
原理
電流\(I\) が流れている物質に磁界\(B\) を加えると、電流を形成するキャリア(正孔・電子)がローレンツ力を受けます。
ローレンツ力を受けたキャリアは、物質の端に移動するため、物質内に起電力が発生します。
発生した起電力によって電界も生じるため、キャリアはクーロン力(静電気力)も受けます。
ローレンツ力と、クーロン力の方向は逆方向を向くため、ちょうど打ち消す大きさの起電力で、物質の端の電位は安定します。
電位が発生する原理の解析
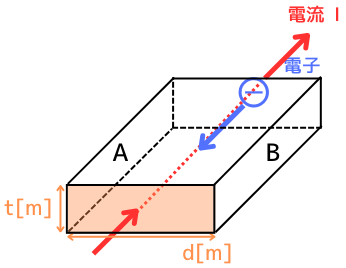
磁界を加えられていないとき
左図のような直方体で、電子がキャリアのN型半導体について考えていきます。
磁界が加えられていないとき、電流\(I[A]\)が流れていても、A面・B面にはキャリアの偏りがないため、電位は発生しません。
流れている電流\(I[A]\)は、電子の電気素量\(e[C]\)、電子の密度\(n\)[個/\(m^3\)]、電子の速度\(v[m/s]\)、物質の厚さ\(t[m]\)、幅\(d[m]\)としたとき、次のように表されます。
\(I=envtd\) …(1)
変形すると、
\(\displaystyle v=\frac{I}{entd}\) …(2)
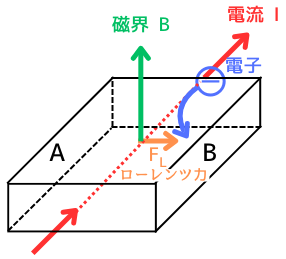
磁束密度\(B[T]\)の磁界を加える
磁束密度\(B[T]\)の磁界を加えると、フレミング左手の法則に従って、電子にローレンツ力\(F_L[N]\)が働いてB面に引き寄せます。
\(F_L=evB\) …(3)
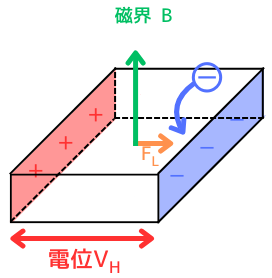
電位\(V_H[V]\)が発生する
キャリアの密度が偏ることによって、A面・B面間に電位\(V_H\)が発生します。
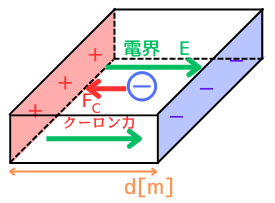
電界強度\(E[V/m]\)の電界が発生する
発生した電位は、A面・B面間に電界強度\(E[V/m]\)の一様な電界を発生させます。
一様な電界における電位\(V_H\)と電界\(E\)の関係は、物質の幅\(d\)を使うと、コンデンサと同じ関係式となります。
\(V_H=Ed\) …(4)
電界\(E\)によって、クーロン力\(F_C[N]\)が働いてA面に引き寄せます。電子の電荷の大きさは電気素量\(e[C]\)なので、
\(F_C=eE\) …(5)
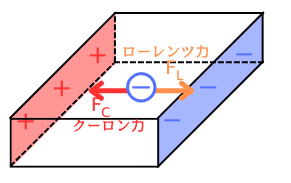
ローレンツ力\(F_L[N]\)とクーロン力\(F_C[N]\)が均衡する
B面に引き寄せるローレンツ力\(F_L\)と、A面に引き寄せるクーロン力\(F_C\)が均衡します。
(3)式=(5)式となるので、
\(evB=eE\)
⇔\(vB=E\) …(6)
(6)式を(4)式に代入すると、電位\(V\)が求まります。
\(V_H=Ed=vBd\) …(7)
(7)式に(2)式を代入して電子の速度\(v\)を消すと、
\(\displaystyle V_H=vBd=\frac{I}{entd} Bd=\frac{IB}{ent}\) …(8)
以上より、ホール効果で得られる電位\(V_H\)が求まりました。
(8)式の\(e\)、\(n\)、\(t\)は、固定値なので、一定の磁束密度\(B\)を与えるようにした場合、
電位\(V_H\)と電流\(I\)は比例関係となります。(\(V_H∝I\))
このことから、電流値そのものを測定することも可能です。
キャリアが正孔であるP型半導体でホール効果を起こした場合
N型半導体のキャリアである電子の電気素量は、\(-e\)であるのに対し、
P型半導体のキャリアである正孔の電気素量は、\(+e\)です。
そのため、N型半導体とは逆に、A面が-、B面が+となるため、電位の正負が逆になります。
関連記事(その他)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント