【電験三種：理論】平成２１年度　問９

難易度

交流波形の瞬時値に関する問題です。
高校数学の基礎問題級のレベルですが、三角関数のラジアン表記に慣れていないと少々手間取ります。
手間取ったとしても、この問題は確実に解きたい問題です。

問題

ある回路に、\(i=4\sqrt{2}sin120\pi t[A]\)の電流が流れている。
この電流の瞬時値が、\(t=0[s]\)以降に初めて\(4[A]\)となるのは、時刻\(t=t_1[s]\)である。
\(t_1[s]\)の値として、正しいのは次のうちどれか。

(1)\(\displaystyle \frac{1}{480}\)　　　(2)\(\displaystyle \frac{1}{360}\)　　　(3)\(\displaystyle \frac{1}{240}\)　　　(4)\(\displaystyle \frac{1}{160}\)　　　(5)\(\displaystyle \frac{1}{120}\)

回答

答え

(１)

回答方針

①\(i=4[A]\)を、問題の式に代入する。
②\(4[A]\)のときの\(sin120\pi t_1\)の値がわかる。
③このときの\(t_1\)を計算する。

要点整理

ラジアンについて
１ラジアンは、円の半径の長さに等しい弧に対する中心角の大きさです。
単位は\([rad]\)であり、ラジアンで表記する方法を、弧度法と呼びます。
文字で書いてもよくわからないので、図にすると、下の図となります。

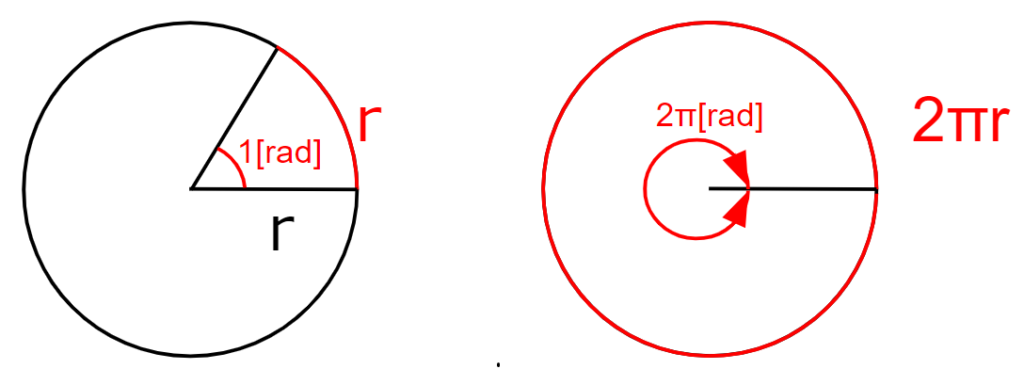
度数法\(\theta[°]\)、弧度法\(ωt[rad]\)、対応する\(sin ωt\)、\(tan ωt\)を表にまとめると下記の通りです。

\(\theta[°]\)	\(ωt[rad]\)	\(sinωt\)	\(tanωt\)
\(0\)	\(0\)	\(0\)	\(0\)
30	\(\displaystyle \frac{\pi}{6}\)	\(\displaystyle \frac{1}{2}\)	\(\displaystyle \frac{1}{\sqrt{3}}\)
45	\(\displaystyle \frac{\pi}{4}\)	\(\displaystyle \frac{1}{\sqrt{2}}\)	\(1\)
60	\(\displaystyle \frac{\pi}{3}\)	\(\displaystyle \frac{\sqrt{3}}{2}\)	\(\sqrt{3}\)
90	\(\displaystyle \frac{\pi}{2}\)	\(0\)	\(\infty\)
180	\(\pi\)	\(0\)	\(0\)
360	\(2\pi\)	\(0\)	\(0\)

---

瞬時値\(i(t)\)に関連するパラメータについて

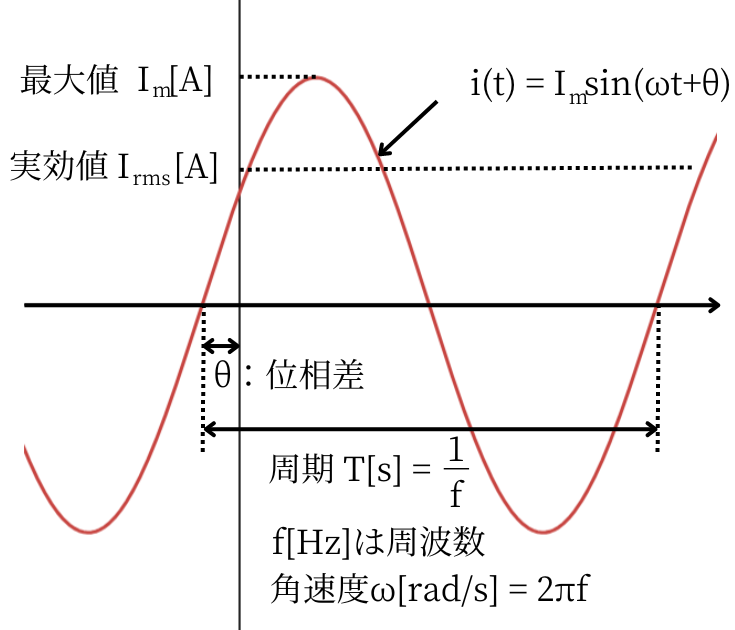
最大値 \(I_m\)は、基準値 \(i(t)=0[A]\)の時から一番大きな値を最大値と呼びます。
「電流の大きさ」や、「電圧の大きさ」と呼ぶような時は、最大値を指します。

位相差 \(\theta\)は、基準となる位相に対するズレの事です。
回路の負荷に、コイルやコンデンサ等の負荷があると、電圧と電流の間に位相差が発生します。

周期 \(T[s]\)は、電圧・電流の波形が１回上下して戻るまでの時間です。
周波数 \(f[Hz]\)は、電圧・電流の波形が１秒間に上下を繰り返す回数です。
周期とは逆数の関係にあり、\(\displaystyle T=\frac{1}{f}\)の式で表されます。

角速度 \(ω[rad/s]\)は、１秒間辺りに回転した速度のことです。
周波数とは、\(ω=2\pi f\)の関係があり、頻繁に使用します。

実効値 \(I_{rms}\)
交流は電圧も電流も常に変化し続けるため、供給される電力を瞬時値を使って計算することは大変です。また、単純に平均値を取っても、周期的な正弦波なので０になります。
そのため、ある電気抵抗に交流を加えた場合の1周期における平均電力と、同じ抵抗に直流を加えた場合の電力が等しくなったとき、直流と同じ値となるように定義したものが実効値です。
\(\displaystyle I_{rms}=\sqrt{\frac{1}{T}\int_0^{T}i(t)^2dt}\)

ぱっと見複雑な式ですが、意味を分解していけば理解も簡単です。
１周期分の瞬時値を足して、周期\(T\)で割れば、定義通りに直流と同じ値を取り出せそうです。
しかし、交流の場合は、プラス・マイナスを繰り返すので単純に足すだけでは０になってしまいます。
それを解決するため、瞬時値を二乗して\(i(t)^2\)とします。
次に、１周期分の瞬時値を足すため、１周期分の積分をして、周期\(T\)で割ります。
\(\displaystyle \frac{1}{T}\int_0^{T}i(t)^2dt\)
最後に、瞬時値を二乗してから積分計算をしたので、√することで元に戻します。
\(\displaystyle I_{rms}=\sqrt{\frac{1}{T}\int_0^{T}i(t)^2dt}\)
これで完成です。

要点整理の適用

\(i=4\sqrt{2}sin120\pi t_1[A]\)の式に、\(i=4[A]\)を、問題の式に代入します。
\(4=4\sqrt{2}sin120\pi t_1[A]\)
⇔\(\displaystyle sin120\pi t_1=\frac{1}{\sqrt{2}}\)

\(\displaystyle sin120\pi t_1=\frac{1}{\sqrt{2}}\)となるのは、\(\displaystyle 120\pi t_1 =\frac{\pi}{4}\)のときです。

\(\displaystyle t_1 =\frac{\pi}{4}・\frac{1}{120\pi}=\frac{1}{480}\)

以上より、\(\displaystyle t_1 =\frac{1}{480}\)ですので、答えは(1)です。

出典元

平成２１年度第三種電気主任技術者試験　理論科目Ａ問題問９

参考書

本ブログの管理人は、電験３種過去問マスタを使って３種を取りました。
とても解説が分かり易い参考書なのでお勧めです。

電験3種過去問マスタ 理論の20年間
電験3種過去問マスタ 電力の20年間
電験3種過去問マスタ 機械の20年間
電験3種過去問マスタ 法規の15年間