【電験三種：理論】平成２１年度　問８

難易度

交流回路で、インダクタンスを使用した問題です。
交流回路の問題としては、基礎レベルですが、初学者には位相角を計算する問題は取っ付きづらいかもしれません。

主に問われる知識は３点。
①インピーダンス$Z$と、インダクタンス$L$の関係を理解すること
②複素数の計算を理解すること
③位相角計算について理解すること

難易度としては普通程度だと思われます。
合格するには、確実に解きたい問題です。

問題

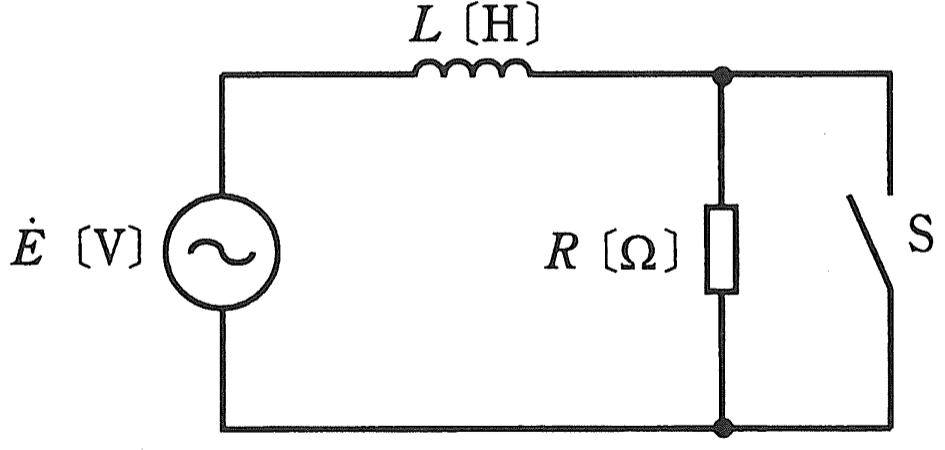
図のように、$R=\sqrt{3}ωL[Ω]$の抵抗、インダクタンス$L[H]$のコイル、スイッチSが角周波数$ω[rad/s]$の交流電圧$\dot{E}[V]$の電源に接続されている。
スイッチSを開いているとき、コイルを流れる電流の大きさを$I_1[A]$、電源電圧に対する電流の位相差を$\theta_1[°]$とする。
また、スイッチSを閉じているとき、コイルを流れる電流の大きさを$I_2[A]$、電源電圧に対する電流の位相差を$\theta_2[°]$とする。
このとき、$\frac{I_1}{I_2}$及び$|\theta_1-\theta_2|[°]$の値として、正しいものを組み合わせたのは次のうちどれか。

	$\frac{I_1}{I_2}$	$|\theta_1-\theta_2|$
(1)	$\frac{1}{2}$	30
(2)	$\frac{1}{2}$	60
(3)	2	30
(4)	2	60
(5)	2	90

回答

答え

(2)

回答方針

①スイッチSが開いているとき、閉じているときの図を書いて、負荷を確認します。
②スイッチが開いているときのインピーダンス$\dot{Z_1}$を求めます。
③オームの法則から、スイッチSが開いているときの電流$\dot{I_1}$を求めます。
④電流$\dot{I_1}$から、電流の大きさと、位相角$\theta_1$を出します。
⑤同様に、スイッチが閉じているときのインピーダンス$\dot{Z_2}$を求めます。
⑥スイッチSが閉じているときの電流$\dot{I_2}$を求めます。
⑦電流$\dot{I_2}$から、電流の大きさと、位相角$\theta_2$を出します。
⑧$\frac{I_1}{I_2}$、$|\theta_1-\theta_2|$を計算で完了です。

要点整理

インピーダンスと、インダクタンス、キャパシタンスの関係について要点整理します。

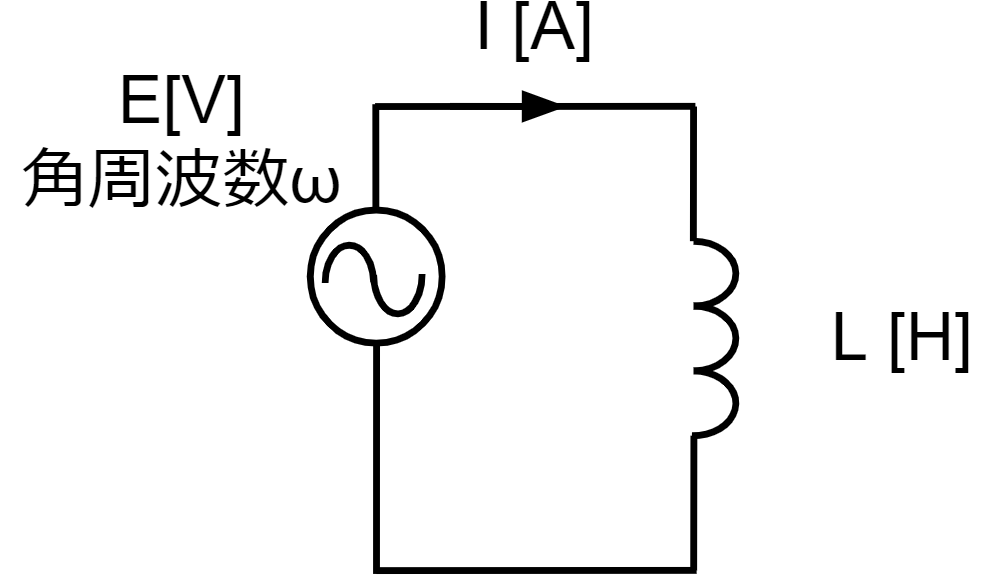左図のように、電圧の大きさ$E$、角周波数$ω$の電源に、インダクタンス$L[H]$のコイルが接続されているとします。 電源の角周波数は$ω[rad/s]$であるため、 回路のインピーダンス$\dot{Z}[Ω]$は、$\dot{Z}=jωL$です。 この時の電流値$\dot{I}[A]$は、 $\displaystyle \dot{I}=\frac{\dot{E}}{\dot{Z}}=\frac{E}{jωL}=\frac{E}{jωL}・\frac{j}{j}=\frac{jE}{-ωL}=-j\frac{E}{ωL}$ つまり、$\displaystyle \dot{I}=-j\frac{E}{ωL}$となります。 複素数の$j$は、プラスだと進み、マイナスだと遅れを表します。 電流の式中の$-j$から、電源をコイルだけに接続した回路は、電流が電圧に対して位相が90°遅れていることがわかります。

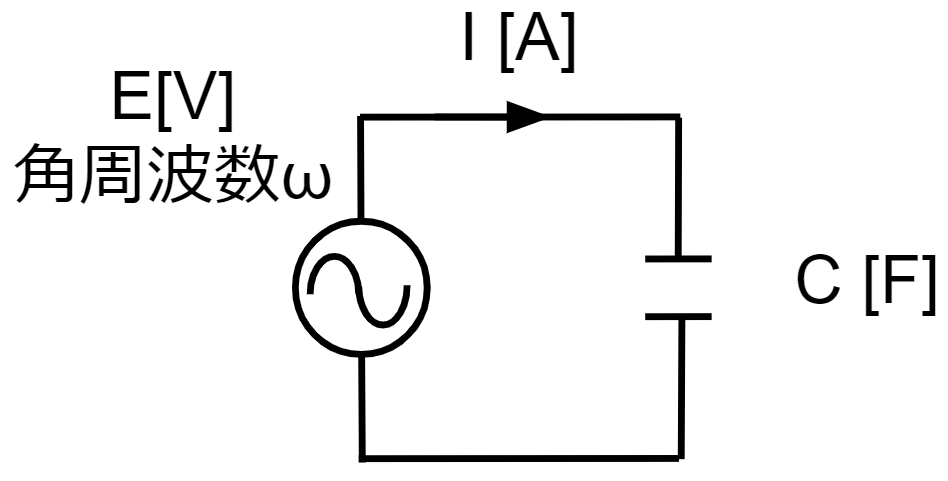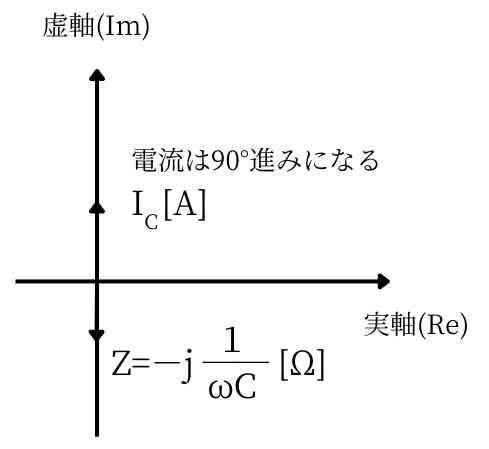左図のように、電圧の大きさ$E$、角周波数$ω$の電源に、キャパシタンス$C[F]$のコンデンサが接続されているとします。 電源の角周波数は$ω[rad/s]$であるため、 回路のインピーダンス$\dot{Z}[Ω]$は、$\displaystyle \dot{Z}=\frac{1}{jωC}$です。 この時の電流値$\dot{I}[A]$は、 $\displaystyle \dot{I}=\frac{\dot{E}}{\dot{Z}}=jωCE$ つまり、$\displaystyle \dot{I}=jωCE[A]$となります。 複素数の$j$は、プラスだと進み、マイナスだと遅れを表します。 電流の式中の$j$から、電源をコンデンサだけに接続した回路は、電流が電圧に対して位相が90°進んでいることがわかります。

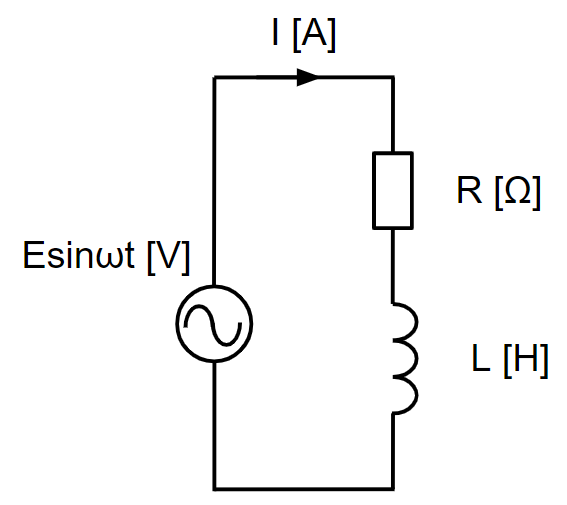RL回路とした場合、インピーダンスは、 $\dot{Z}=R+jωL [Ω]$ となります。 この時の電流値$\dot{I}[A]$は、 $\displaystyle \begin{eqnarray} \dot{I}&=&\frac{E}{Z}=\frac{E}{R+jωL}=\frac{E}{R+jωL}・\frac{R-jωL}{R-jωL}\\ &=&\frac{R-jωL}{R^2+(ωL)^2}・E…(A) \end{eqnarray}$ となります。 この時の電流の大きさを求めます。三平方の定理から、 $\displaystyle I=\frac{1}{\sqrt{R^2+(ωL)^2}}・E$となります。 位相角$\angle I$を求めます。 まずは各項の位相角を出します。 位相角の出し方は、$\displaystyle tan^{-1}\frac{虚数部}{実数部}$です。 つまり、$\angle (X+jY)$としたとき、$\displaystyle tan^{-1}\frac{Y}{X}$となります。 これを、(A)式の各項に反映させると、 ・$R-jωL$　⇒　$\displaystyle -tan^{-1}\frac{ωL}{R}$ ・$R^2+(ωL)^2$　⇒　$tan^{-1}0 =0$ ・$E$　⇒　$tan^{-1}0 =0$ となるので、まとめると、 $\displaystyle \angle I =\angle (R-jωL) -\angle[R^2+(ωL)^2] +\angle E$ となるので、 $\displaystyle \angle I =-tan^{-1}\frac{ωL}{R}-\tan^{-1}0+\tan^{-1}0=-tan^{-1}\frac{ωL}{R}$となります。 したがって、$\displaystyle \angle I =-tan^{-1}\frac{ωL}{R}$となります。

要点整理の適用

スイッチSが開いているときの図を書いて、負荷を確認します。

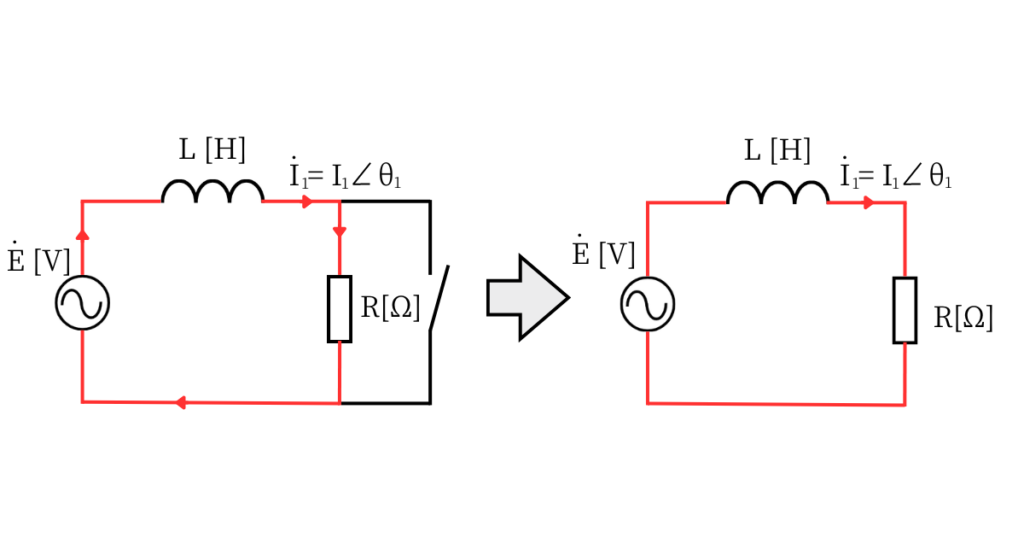
図１

図1は、スイッチSが開いているときの図です。
スイッチのある回路には電流は流れないため、全て抵抗$R[Ω]$を通って流れます。

スイッチS開時の、回路のインピーダンス$\dot{Z}_1$は、$\dot{Z}_1=R+jωL$です。

この時の電流$\dot{I_1}$は、
$\displaystyle \dot{I_1}=\frac{\dot{E}}{\dot{Z}_1}=\frac{\dot{E}}{R+jωL}$

問題の条件から、$R=\sqrt{3}ωL[Ω]$なので、
$\displaystyle \begin{split} \dot{I_1}&=&\frac{\dot{E}}{\sqrt{3}ωL+jωL}=\frac{\dot{E}}{(\sqrt{3}+j)ωL}\\ &=&\frac{\dot{E}}{(\sqrt{3}+j)ωL}・\frac{\sqrt{3}-j}{\sqrt{3}-j}=\frac{\dot{E}}{(3+1)ωL}・(\sqrt{3}-j)\\ &=&\frac{\dot{E}}{4ωL}・(\sqrt{3}-j) \end{split}$

ここで、$\dot{E}=E$とすると、
$\displaystyle \dot{I_1}=\frac{E}{4ωL}・(\sqrt{3}-j)$　となります。

電流の大きさ$I_1$は、
$\displaystyle I_1=\frac{E}{4ωL}・\sqrt{\sqrt{3}^2+1^2} =\frac{E}{2ωL}$
したがって、$\displaystyle I_1=\frac{E}{2ωL}$となります。

電源電圧に対する電流の位相差$\theta_1[°]$は、
$\displaystyle \begin{split} \theta_1&=&\angle\dot{I}_1=\frac{\angle E}{\angle 4ωL}・\angle(\sqrt{3}-j) =\angle E-\angle 4ωL+\angle(\sqrt{3}-j)\\ &=&tan^{-1} 0-tan^{-1} 0+tan^{-1} \frac{-1}{\sqrt{3}}=-tan^{-1}\frac{1}{\sqrt{3}}=-30[°] \end{split}$
したがって、$\theta_1=-30[°]$となります。

---

スイッチSが閉じているときの図を書いて、負荷を確認します。

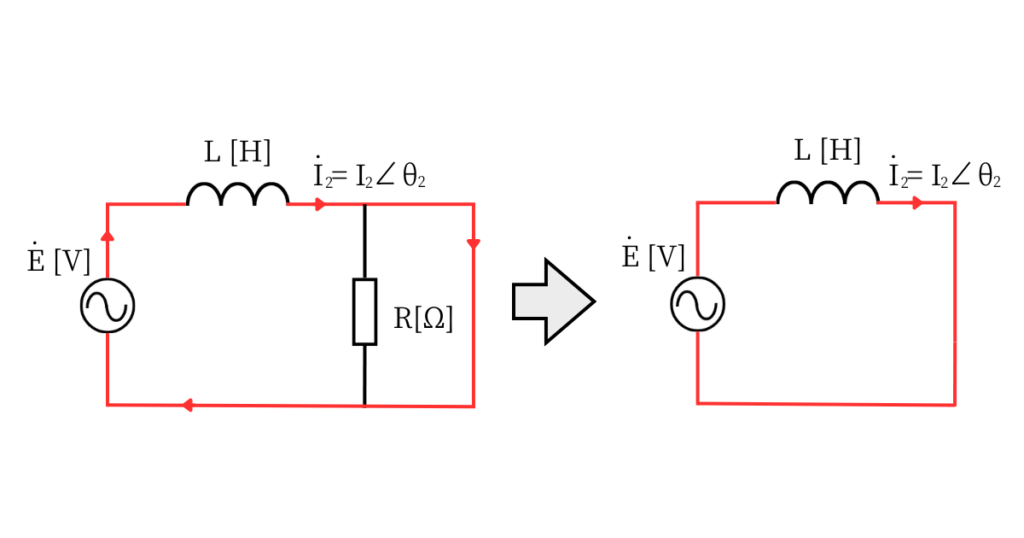
図2

図2は、スイッチSが閉じているときの図です。
スイッチのある回路に全て電流が流れるため、全て抵抗$R[Ω]$は無視されます。

そのため、スイッチS閉時の、回路のインピーダンス$\dot{Z}_2$は、$\dot{Z}_2=jωL$です。

この時の電流$\dot{I_2}$は、
$\displaystyle \dot{I_2}=\frac{\dot{E}}{\dot{Z}_2}=\frac{\dot{E}}{jωL}$

ここで、$\dot{E}=E$とすると、
$\displaystyle \dot{I_2}=\frac{E}{jωL}=-j\frac{E}{ωL}$　となります。

電流の大きさ$I_2$は、
$\displaystyle I_2=\frac{E}{ωL}$となります。

電源電圧に対する電流の位相差$\theta_2[°]$は、
$\displaystyle \begin{split} \theta_2=\angle\dot{I}_2=\angle (-j)・\frac{\angle E}{\angle ωL}=\angle (-j)+\angle E-\angle ωL =-90+0-0=-90[°] \end{split}$
したがって、$\theta_2=-90[°]$となります。

---

最後に、
$\displaystyle I_1=\frac{E}{2ωL}$、$\theta_1=-30[°]$

$\displaystyle I_2=\frac{E}{ωL}$、$\theta_2=-90[°]$
がわかったので、$\frac{I_1}{I_2}$と、$|\theta_1-\theta_2|$を求めます。

$\displaystyle \frac{I_1}{I_2}=\frac{\frac{E}{2ωL}}{\frac{E}{ωL}}=\frac{1}{2}$
$|\theta_1-\theta_2|=$$-30-(-90)=$$60$

となりますので、答えは(2)です。

出典元

平成２１年度第三種電気主任技術者試験　理論科目Ａ問題問８

参考書