難易度
直流の抵抗回路に関する基礎知識問題です。
高校レベルなので、確実に回答したい問題です。
問題
抵抗値が異なる抵抗\(R_1[Ω]\)と\(R_2[Ω]\)を図１のように直列に接続し、\(30[V]\)の直流電圧を加えたところ、回路に流れる電流は\(6[A]\)であった。
次に、この抵抗\(R_1[Ω]\)と\(R_2[Ω]\)を図２のように並列に接続し、\(30[V]\)の直流電圧を加えたところ、回路に流れる電流は\(25[A]\)であった。
このとき、抵抗\(R_1[Ω]\)、\(R_2[Ω]\)のうち小さい方の抵抗\([Ω]\)の値として正しいのは次のうちどれか。
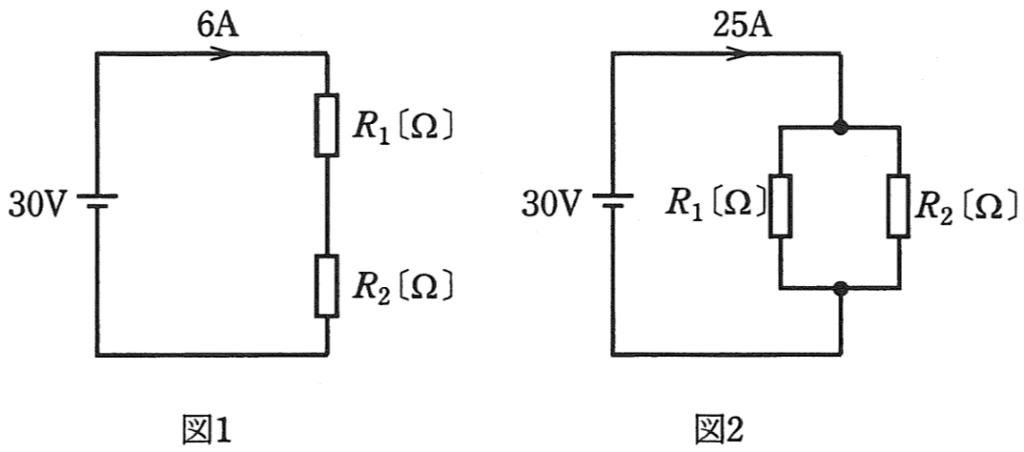
(1)1 (2)1.2 (3)1.5 (4)2 (5)3
回答
答え
(4)
回答方針
図１の電圧と電流値から直列抵抗の合成抵抗がわかります。
図２の電圧と電流値から並列抵抗の合成抵抗がわかります。
それぞれがわかれば、連立方程式で解くことができます。
要点整理
直列接続と、並列接続の時の合成抵抗の計算方法をまとめます。
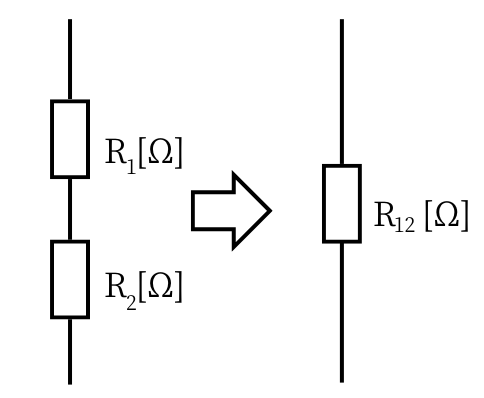 | 直列接続された抵抗の合成抵抗の計算方法をまとめます。 抵抗\(R_1[Ω]\)と、抵抗\(R_2[Ω]\)が直列接続されているときの合成抵抗を\(R_{12}[Ω]\)とした時 \(R_{12}=R_1+R_2[Ω]\) |
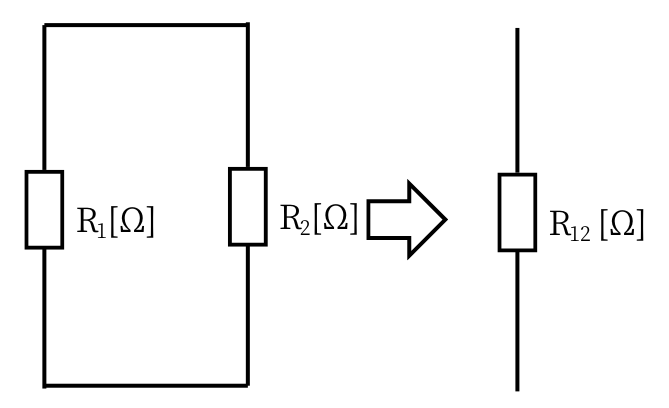 | 並列接続された抵抗の合成抵抗の計算方法をまとめます。 抵抗\(R_1[Ω]\)と、抵抗\(R_2[Ω]\)が並列接続されているときの合成抵抗を\(R_{12}[Ω]\)とした時 \(\displaystyle \frac{1}{R_{12}}=\frac{1}{R_1}+\frac{1}{R_2}\) まとめると、 \(\displaystyle R_{12}=\frac{R_1R_2}{R_1+R_2}[Ω]\) となります。 |
要点整理の適用
図１から、直列の合成抵抗値を求めます。
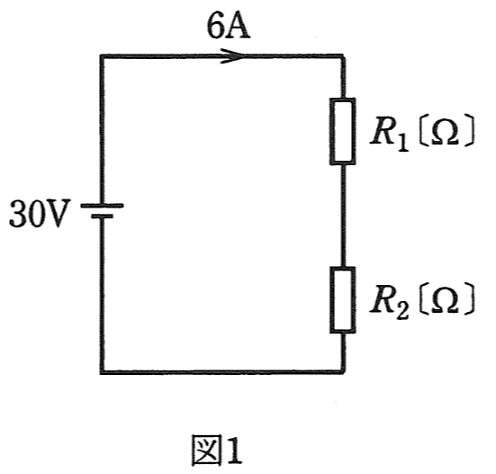
\(R_1\)と\(R_2\)の合成抵抗\(R_{12s}\)は、
\(R_{12s}=R_1+R_2\)…①
オームの法則に、①を代入し、
\(30=6・R_{12s}=6(R_1+R_2)\)
となります。したがって、
\(R_1+R_2＝5[Ω]\)…②
次に、図2から、並列の合成抵抗値を求めます。
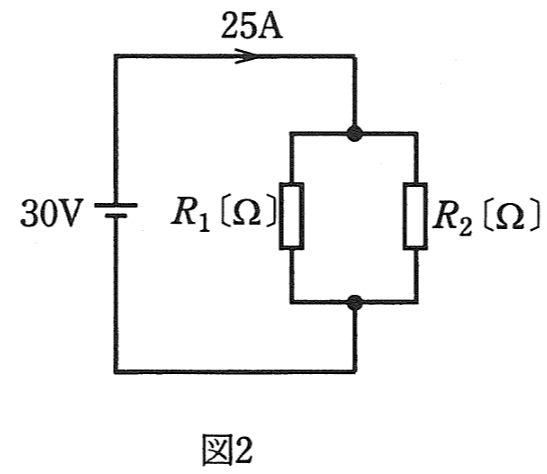
\(R_1\)と\(R_2\)の合成抵抗\(R_{12p}\)は、
\(\displaystyle R_{12p}=\frac{R_1R_2}{R_1+R_2}\)…③
オームの法則に、③を代入し、
\(\displaystyle 30=25・R_{12p}=25\frac{R_1R_2}{R_1+R_2}\)…④
④に②を代入し、
\(\displaystyle 30=25\frac{R_1R_2}{5}\)
⇔ \(6=R_1R_2\)…⑤
整理すると、
\(\begin{eqnarray}
\left \{
\begin{array}{l}
R_1+R_2＝5…②\\
R_1R_2=6…⑤
\end{array}
\right.
\end{eqnarray}\)
となるので、②を変形すると、
\(R_2＝5-R_1\)
となるので、⑤に代入します。
\(R_1・(5-R_1)=6\)
⇔ \(-R_1^2+5R_1-6=0\)
⇔ \(R_1^2-5R_1+6=0\)
⇔ \((R_1-2)(R_1-3)=0\)
したがって、\(R_1\)は、\(R_1=2,3\)となります。
\(R_1=2\)のとき、\(R_2=3\)
\(R_1=3\)のとき、\(R_2=2\)
となるので、
小さい方の抵抗[Ω]は、2[Ω]です。
出典元
平成２１年度第三種電気主任技術者試験 理論科目Ａ問題問６
参考書
本ブログの管理人は、電験３種過去問マスタを使って３種を取りました。
とても解説が分かり易い参考書なのでお勧めです。
| 電験3種過去問マスタ 理論の20年間 |  |
| 電験3種過去問マスタ 電力の20年間 | |
| 電験3種過去問マスタ 機械の20年間 | |
| 電験3種過去問マスタ 法規の15年間 | |
コメント