難易度
コイルの磁束鎖交数と、蓄えられる磁気エネルギーに関する基礎知識問題です。
ひねりは特にないので、確実に回答したい問題です。
問題
インダクタンス\(1[mH]\)のコイルに直流電流\(10[A]\)が流れているとき、このコイルの磁束鎖交数\(ψ_1[Wb]\)は ア \([Wb]\)である。
また、コイルに蓄えられている磁気エネルギー\(W_1[J]\)は イ \([J]\)である。
次に、このコイルに流れる直流電流を\(30[A]\)とすると、磁束鎖交数\(ψ_2[Wb]\)と蓄えられる磁気エネルギー\(W_2[J]\)はそれぞれ ウ となる。
上記の記述中の空白箇所(ア)、(イ)及び(ウ)に当てはまる語句
又は数値として、正しいものを組合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | \(5\times10^{-3}\) | \(5\times10^{-2}\) | \(ψ_2はψ_1の3倍、W_2はW_1の9倍\) |
| (2) | \(1\times10^{-2}\) | \(5\times10^{-2}\) | \(ψ_2はψ_1の3倍、W_2はW_1の9倍\) |
| (3) | \(1\times10^{-2}\) | \(1\times10^{-2}\) | \(ψ_2はψ_1の9倍、W_2はW_1の3倍\) |
| (4) | \(1\times10^{-2}\) | \(5\times10^{-1}\) | \(ψ_2はψ_1の3倍、W_2はW_1の9倍\) |
| (5) | \(5\times10^{-2}\) | \(5\times10^{-1}\) | \(ψ_2はψ_1の9倍、W_2はW_1の27倍\) |
回答
答え
(2)
回答方針
磁束鎖交数と磁気エネルギーの基本的な式を覚えていれば回答出来るような内容です。
似たような単語が多く、記憶した内容がごちゃごちゃしやすいので、関連して思い出せるように導出方法も理解することをお勧めします。
また、単位から推察して当てはめる事で、導き出せる場合もあるので、各パラメータの単位も一緒に覚えましょう。
要点整理
コイルに電流を流した時に作り出す磁束や、磁束鎖交数に関する要点を整理します。
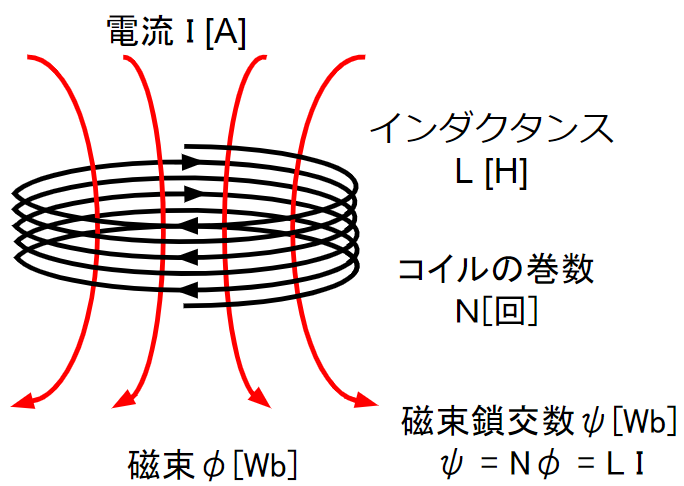 | 左図は、 ・インダクタンス \(L[H]\) ・コイルの巻数 \(N[回]\) のコイルに、 ・電流\(I[A]\)を流した時の ・磁束 \(Φ[Wb]\)のときのイメージ図です。 この時の磁束鎖交数\(ψ[Wb]\)は、\(ψ = N Φ = L I\)の関係があります。 本問では、\(ψ = L I\)の関係を使います。 |
\( N Φ = L I\)の関係式は、磁気回路を扱う上で非常に重要な式です。
逆起電力を使った別アプローチでの覚え方も示しますので、導出出来るようになりましょう。
自己インダクタンス \(L\)のコイルに流れる電流を変化させた時の逆起電力は、\(\displaystyle V=-L\frac{dI}{dt}\)
巻数Nのコイルの磁束を変化させた時の逆起電力は、\(\displaystyle V=-N\frac{dΦ}{dt}\)
この2式から、\(\displaystyle V=-L\frac{dI}{dt}=-N\frac{dΦ}{dt}\)となり、\(N Φ = L I\)が導き出せます。
コイルに蓄えられる磁気エネルギーの要点整理をします。
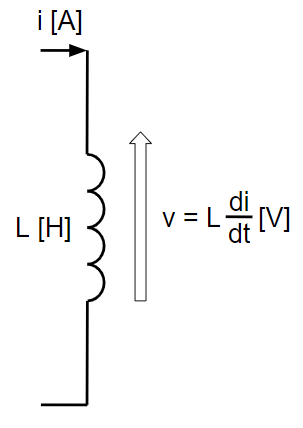 | 左図のように、自己インダクタンス\(L[H]\)のコイルに電流\(i[A]\)を流した時、逆起電力は\(v[V]\)となるコイルに蓄えられるエネルギーを考える。 \(\displaystyle \frac{di}{dt}\)は、流れる電流\(i\)が、\(dt\)秒間に、\(di\)だけ変化したことを表す。 電源がインダクタンスに送る電力\(p[W]\)は、 \(\displaystyle p=v・i=\left(L \frac{di}{dt}\right)・i[W]\) したがって、\(dt\)秒間にコイルが受取るエネルギー\(dw[W]\)は、 \(\displaystyle dw = p・dt = \left(L \frac{di}{dt}\right)・i・dt = L・i・di [J]\) したがって、\(I[A]\)が流れている\(L[H]\)が蓄えるエネルギー\(W[J]\)は、 \(\displaystyle W=\int_{0}^{I} dw=\int_{0}^{I} L・i・di=L\int_{0}^{I} i・di\) \(\displaystyle =L\left[\frac{1}{2}i^2\right]_0^I=\frac{1}{2}LI^2[J]\) 以上より、コイルに蓄えられる磁気エネルギーは\(\displaystyle W=\frac{1}{2}LI^2[J]\)です。 |
要点整理の適用
要点整理で書き出した内容を、各回答に適用します。
ア
磁束鎖交数に関する要点整理から、\(ψ = L I\)の式を使います。
問題文から、
コイルのインダクタンス\(L[H]\)は、\(L=1[mH]=1\times10^{-3}[H]\)
電流\(I[A]\)は、\(I=10[A]\)です。
磁束鎖交数の式に代入して、
\(ψ_1 = L I=\left(1\times10^{-3}\right)・10=\) \(1\times10^{-2}[Wb]\)となります。
イ
磁気エネルギーに関する要点整理から、\(\displaystyle W=\frac{1}{2}LI^2[J]\)の式を使います。
問題文から、
コイルのインダクタンス\(L[H]\)は、\(L=1\times10^{-3}[H]\)、電流\(I[A]\)は、\(I=10[A]\)です。
磁気エネルギーに関する式に代入して、
\(\displaystyle W_1=\frac{1}{2}LI^2=\frac{1}{2}\left(1\times10^{-3}\right)・10^2=0.5\times10^{-1}=\) \(5\times10^{-2}[J]\)となります。
ウ
問題文から、
コイルのインダクタンス\(L[H]\)は、\(L=1\times10^{-3}[H]\)、電流\(I[A]\)は、\(I=30[A]\)です。
磁束鎖交数の式に代入して、
\(ψ_2 = L I=\left(1\times10^{-3}\right)・30=\) \(3\times10^{-2}[Wb]\)となります。
磁気エネルギーに関する式に代入して、
\(\displaystyle W_2=\frac{1}{2}LI^2=\frac{1}{2}\left(1\times10^{-3}\right)・30^2=\) \(45\times10^{-2}[J]\)となります。
以上より、
\(ψ_2\)は、\(ψ_1\)の3倍となり、
\(W_2\)は、\(W_1\)の9倍となります。
以上から、答えは(2)となります。
出典元
平成21年度第三種電気主任技術者試験 理論科目A問題問3
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント