【電験三種：理論】平成２１年度　問１５

難易度

電気計測の単元そのものが取組み難い単元ですが、(a)(b)の２問とも、その中でも難しい問題です。

(a)は、偏位法、零位法と、零位法の測定機器について知っているか否かの知識問題です。
説明文から、動作をイメージすれば、回答に近づけるかもしれません。

(b)ケルビンダブルブリッジ回路の証明問題です。
問題文が非常に長い上、問題文を理解しながら読み進めないと回答できません。
この手の問題は、落ち着いて取り組むことが必須です。
問題文のインパクトが大きいですが、しっかり読み進めれば回答できる難易度です。
解けたとしても確実に時間が掛かるため、他の問題を解いてから、最後に回答すると良いでしょう。

問題

電気計測に関する記述について、次の(a)及び(b)に答えよ。

(a)ある量の測定に用いる方法には各種あるが、指示計器のように測定量を指針の振れの大きさに変えて、その指示から測定量を知る方法を ア 法という。
これに比較して精密な測定を行う場合に用いられている イ 法は、測定量と同種類で大きさを調整できる既知量を別に用意し、既知量を測定量に平衡させて、そのときの既知量の大きさから測定量を知る方法である。
イ 法を用いた測定器の例としては、ブリッジや ウ がある。

上記の記述中の空白箇所（ア）、（イ）及び（ウ）に当てはまる語句として、正しいものを組み合わせたのは次のうちどれか。

	（ア）	（イ）	（ウ）
（１）	偏　位	零　位	直流電位差計
（２）	偏　位	差　動	誘導形電力量計
（３）	間　接	零　位	直流電位差計
（４）	間　接	差　動	誘導形電力量計
（５）	偏　位	零　位	誘導形電力量計

---

(b)図は、ケルビンダブルブリッジの原理図である。
図において、\(R_x[Ω]\)が未知の抵抗、\(R_s[Ω]\)は可変抵抗、\(P[Ω]\)、\(Q[Ω]\)、\(p[Ω]\)、\(q[Ω]\)は固定抵抗である。
このブリッジは、抵抗\(R_x[Ω]\)のリード線の抵抗が、固定抵抗\(r[Ω]\)及び直流電源側の接続線に含まれる回路構成となっており、低い抵抗の測定に適している。

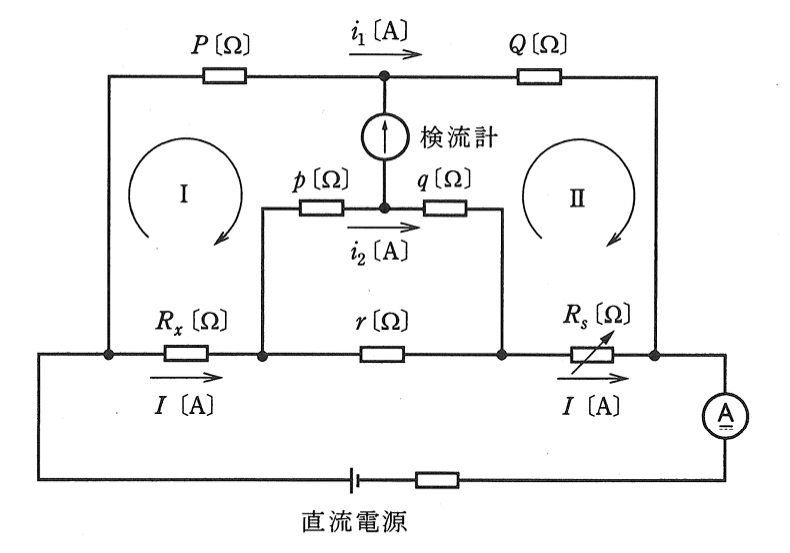
図の回路において、固定抵抗\(P[Ω]\)、\(Q[Ω]\)、\(p[Ω]\)、\(q[Ω]\)の抵抗値が ア \(=0\)の条件を満たしていて、可変抵抗\(R_s[Ω]\)、固定抵抗\(r[Ω]\)においてブリッジが平衡している。この場合は、次式から抵抗\(R_x[Ω]\)が求まる。

\(R_x[Ω]= （\)イ \(）R_s\)

この式が求まることを次の手順で証明してみよう。

[証明]

回路に流れる電流を図に示すように\(I[A]\)、\(i_1[A]\)、\(i_2[A]\)とし、閉回路Ⅰ及びⅡにキルヒホッフの第２法則を適用すると式①、②が得られる。

\(Pi_1=R_xI+pi_2\)　　　………①
\(Qi_1=R_sI+qi_2\)　　　………②

式①、②から

\(\displaystyle \frac{P}{Q}=\frac{R_xI+pi_2}{R_sI+qi_2}=\frac{R_x+p\frac{i_2}{I}}{R_s+q\frac{i_2}{I}}\)　　　………③

また、\(I\)は\((p+q)\)と\(r\)の回路に分流するので、

\((p+q)i_2=r(I-i_2)\)

の関係から式④が得られる。

\(\displaystyle \frac{i_2}{I}=\)ウ　　　………④

ここで\(K=\)ウとし、式③を整理すると式⑤が得られ、抵抗\(R_x[Ω]\)が求まる。

\(R_x=(\)イ\()R_s+(\)ア\()qK\)　　　………⑤

上記の記述中で空白箇所（ア）（イ）及び（ウ）に当てはまる式として、正しいものを組み合わせたのは次のうちどれか。

	（ア）	（イ）	（ウ）
（１）	\(\displaystyle \frac{P}{Q}-\frac{p}{q}\)	\(\displaystyle \frac{P}{Q}\)	\(\displaystyle \frac{r}{p+q+r}\)
（２）	\(\displaystyle \frac{p}{q}-\frac{P}{Q}\)	\(\displaystyle \frac{P}{q}\)	\(\displaystyle \frac{r}{p+r}\)
（３）	\(\displaystyle \frac{p}{q}-\frac{P}{Q}\)	\(\displaystyle \frac{Q}{p}\)	\(\displaystyle \frac{q}{q+r}\)
（４）	\(\displaystyle \frac{P}{Q}-\frac{q}{p}\)	\(\displaystyle \frac{Q}{P}\)	\(\displaystyle \frac{r}{p+q+r}\)
（５）	\(\displaystyle \frac{P}{Q}-\frac{p}{q}\)	\(\displaystyle \frac{P}{Q}\)	\(\displaystyle \frac{p}{p+q+r}\)

回答

答え

問(a)　(1)
問(b)　(1)

要点整理　問(a)

偏位法・零位法について

偏位法は、電圧計や電流計のように測定量を指示針の振れ幅に変換して計器の指示値を読むような方法です。
指示値を読むだけで簡単という長所はありますが、精度が悪いという短所があります。
これは、電流計であれば、測定量（回路に流れる電流）を指示針を振るためのエネルギーとして変換します。その結果、電流計が回路から受取ったエネルギーの分だけ誤差を発生させます。そのため、精度が悪くなってしまうわけです。

零位法は、直流電位差計や、ケルビンダブルブリッジ回路による方法のように、回路を平衡させて検知する方法です。
測定量と、基準量が等しくなって平衡するまで調整する手間があるものの、平衡した測定回路は測定対象からエネルギーを取ることなく測定ができるため、測定対象に与える影響が小さく精度良く測定できます。

計測方法	長所	短所	測定機器例
偏位法	測定が簡単	精度が良くない	可動コイル形電圧計・電流計
零位法	高精度	測定に時間がかかる	直流電位差計 ブリッジ回路（カッコ内は測定対象） ・ホイートストンブリッジ（中抵抗） ・ケルビンダブルブリッジ（低抵抗） ・ウィーンブリッジ（容量、周波数） ・シェーリングブリッジ（静電正接\(tanδ\)）

---

直流電位差計について要点整理します。

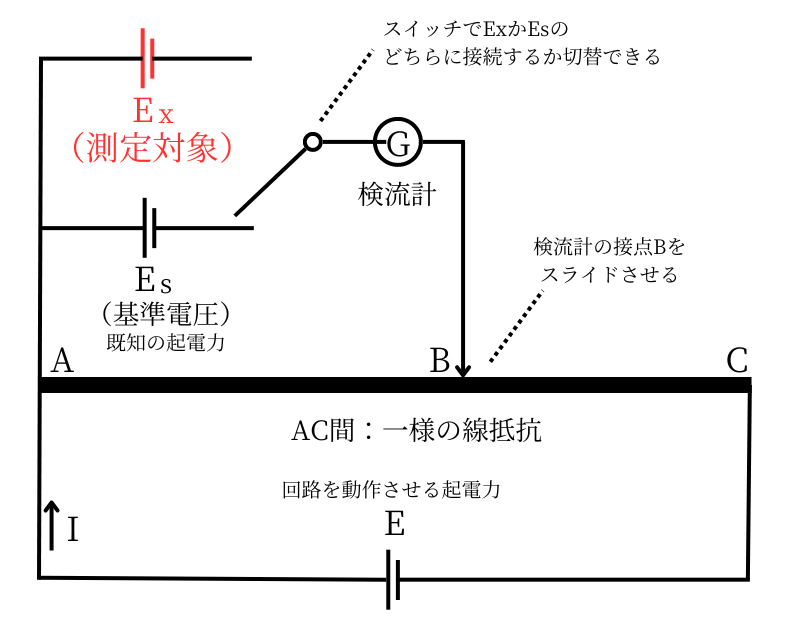	・\(E_x\)を測定対象 ・\(E_s\)は基準電圧（既知の起電力） ・Gは検流計 ・AC間は一様の線抵抗 ・Eは電位差計を動作させるための起電力です。 ・スイッチによって、検流計は\(E_x\)か\(E_s\)のどちらかに接続されます。
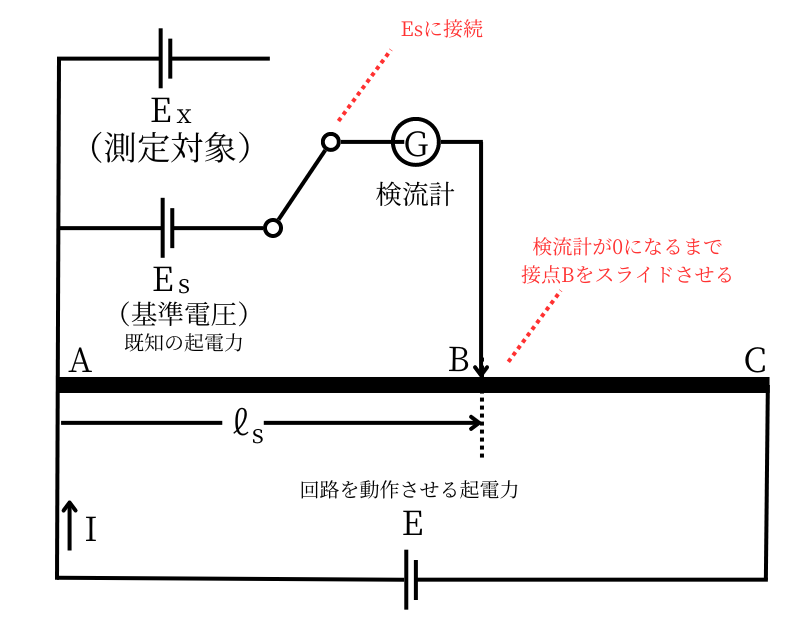	まず初めに、検流計\(G\)を、基準電圧\(E_s\)に接続します。そして、検流計の指示が０になるまで、接点Bをスライドさせます。 検流計の指示が０になったとき、 AB間の抵抗を\(R_s[Ω]\) AB間の長さを\(l_s[m]\)とします。 検流計が０を指しているときは、\(E_s\)から抵抗AB間に電流は流れていません。 つまり、\(E_s\)は、電流\(I\)が作るAB間の抵抗の電圧降下\(R_sI\)と等しくなります。 したがって、次の式が成り立ちます。 \(E_s=R_sI\)　　　………① 変形すると、 \(\displaystyle I=\frac{E_s}{R_s}\)　　　………②
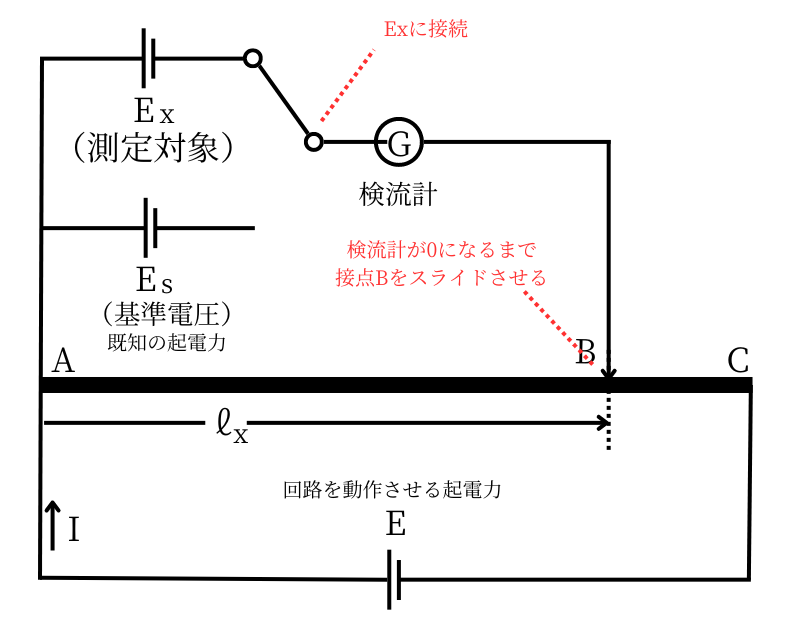	次に、検流計\(G\)を、基準電圧\(E_x\)に接続します。 検流計の指示が０になるまで、接点Bをスライドさせます。 検流計の指示が０になったとき、 AB間の抵抗を\(R_x[Ω]\) AB間の長さを\(l_x[m]\)とします。 このとき、次の式が成り立ちます。 \(E_x=R_xI\)　　　………③ 変形すると、 \(\displaystyle I=\frac{E_x}{R_x}\)　　　………④ ②・④式から、 \(\displaystyle \frac{E_x}{R_x}=\frac{E_s}{R_s}\) が成り立ち、変形すると、 \(\displaystyle E_x=\frac{R_x}{R_s}E_s\)　　　………⑤ AB間の距離の長さが、抵抗の大きさになるので、 \(\displaystyle \frac{R_x}{R_s}=\frac{l_x}{l_s}\)　　　………⑥ ⑥式を⑤式に代入すると \(\displaystyle E_x=\frac{l_x}{l_s}E_s\)　　　………⑦ となります。 例えば、\(E_s=10[V]\)で、\(l_x=1.5\)、\(l_s=1\)とすれば、⑦式から\(E_x=15[V]\)とわかります。

要点整理　問(b)

ケルビンダブルブリッジ回路について

ケルビンダブルブリッジ回路は、零位法の測定回路です。
ホイートストンブリッジ回路を２つ重ねたような回路であるため、ダブルブリッジ回路と呼びます。

この回路は、数mΩ以下の低抵抗を測定するために使用します。
電線は良導体ですが数mΩ程度の抵抗を持っています。そのため、電線の影響を受けると大きな測定誤差が発生してしまいます。
そこで、電線の影響を受けないように工夫された回路がダブルブリッジ回路なわけです。

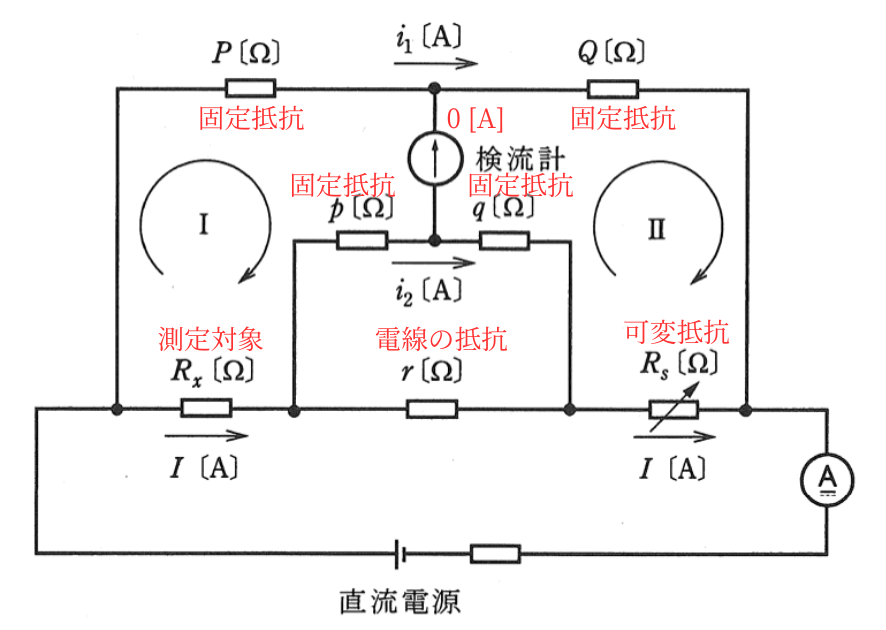	左図の通り、 ・測定対象\(R_x\) ・４つの固定抵抗\(P,Q,p,q\) ・可変抵抗\(R_s\) ・電線の抵抗\(r\) から、ケルビンダブルブリッジ回路は構成されます。 この回路は、誤差の原因となる電線の抵抗\(r\)の影響を除去するための工夫がされています。 これから、最終的な\(R_x\)の数式に\(r\)が出てこない事を示します。
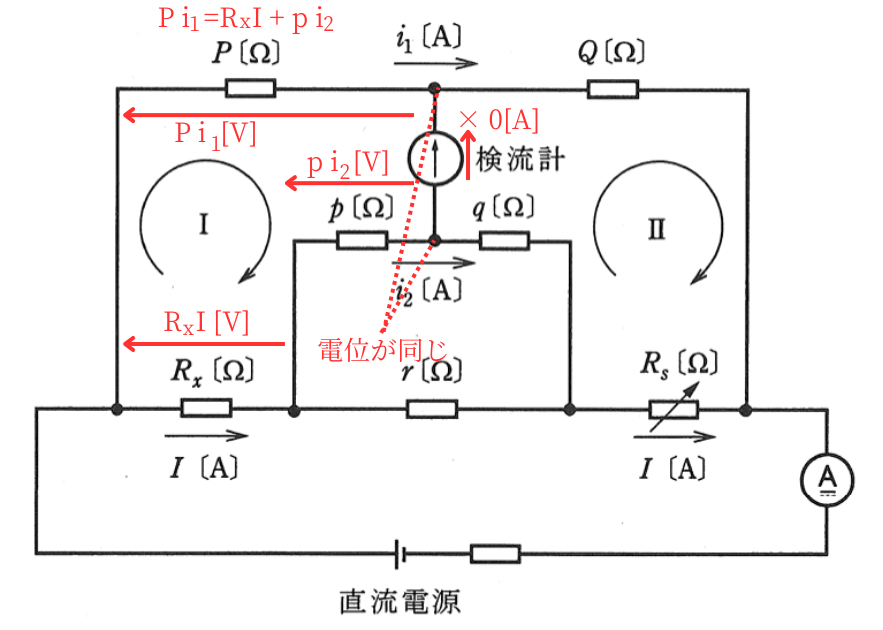	閉回路Ⅰから、 \(Pi_1=R_xI+pi_2\)　　　………① が成り立ちます。
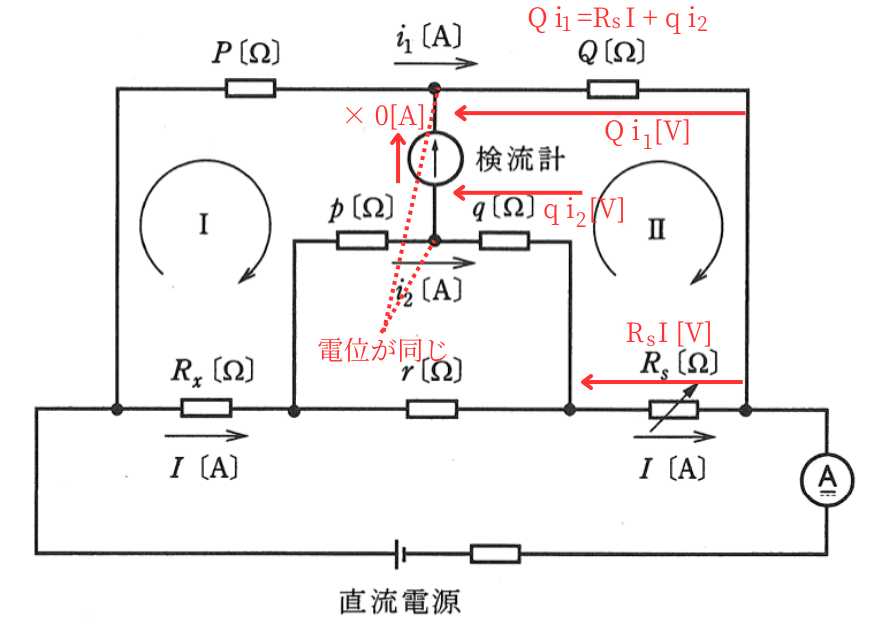	閉回路Ⅱから、 \(Qi_1=R_sI+qi_2\)　　　………② が成り立ちます。 式①、②から、 \(\displaystyle \frac{Pi_1}{Qi_1}=\frac{R_xI+pi_2}{R_sI+qi_2}\) ⇔\(\displaystyle \frac{P}{Q}=\frac{R_x+p\frac{i_2}{I}}{R_s+q\frac{i_2}{I}}\)　　　……③
	\(I\)は\((p+q)\)と\(r\)の回路に分流するので、 \((p+q)i_2=r(I-i_2)\) ⇔\(pi_2+qi_2+ri_2=(p+q+r)i_2=rI\) ⇔\(\displaystyle \frac{i_2}{I}=\frac{r}{p+q+r}\)　　　……④ の関係が得られます。 \(\displaystyle K=\frac{r}{p+q+r}\) として③式を整理すると、 \(\displaystyle \frac{P}{Q}=\frac{R_x+pK}{R_s+qK}\) ⇔\(\displaystyle \frac{P}{Q}(R_s+qK)=R_x+pK\) ⇔\(\displaystyle R_x=\frac{P}{Q}R_s+\frac{P}{Q}qK-pK\) ⇔\(\displaystyle R_x=\frac{P}{Q}R_s+(\frac{P}{Q}-\frac{p}{q})qK\)　　……⑤ となり、測定対象\(R_x\)が求まります。 ⑤式から、電線の抵抗\(r\)が除去されていることがわかります。

要点整理の適用　問(a)

要点整理で書き出した内容を、各回答に適用します。

ア
指示計器のように測定量を指針の振れの大きさに変えて、その指示から測定量を知る方法は、偏位法です。
測定対象に取り付ければ即座に測定できるため、時間が掛からないですが、測定対象からエネルギーを受けて動作するため、測定対象に影響を与えます。そのため、測定精度は落ちます。

イ
精密な測定を行う場合に用いられる方法は零位法です。
既知量と測定量を平衡させるための操作があるため、測定に時間が掛かりますが、測定対象に与える影響が小さいため、高精度な測定ができます。

ウ
直流電位差計が零位法を用いた測定器です。
既知の電圧と、一様な線抵抗のスライド距離から、未知の電圧（測定対象）を測定します。

以上から、問(a)は(1)が答えとなります。

要点整理の適用　問(b)

要点整理の証明の計算式から、問題文の空欄に当てはめます。

計算式⑤から、
\(R_x=(\)イ\()R_s+(\)ア\()qK\)
\(\displaystyle R_x=\frac{P}{Q}R_s+(\frac{P}{Q}-\frac{p}{q})qK\)　　……⑤
であるため、
ア\(\displaystyle =(\frac{P}{Q}-\frac{p}{q})\)
イ\(\displaystyle =\frac{P}{Q}\)
です。

計算式④から、
\(\displaystyle \frac{i_2}{I}=\frac{r}{p+q+r}\)　　　……④
であるため、
ウ　\(\displaystyle =\frac{r}{p+q+r}\)
です。

以上から、問(b)は(1)が答えとなります。

出典元

平成２１年度第三種電気主任技術者試験　理論科目B問題問１５

参考書