難易度
電磁気学の、平行平板コンデンサに関する基礎知識問題です。
関係公式を理解していれば、回答には困らないでしょう。
問題
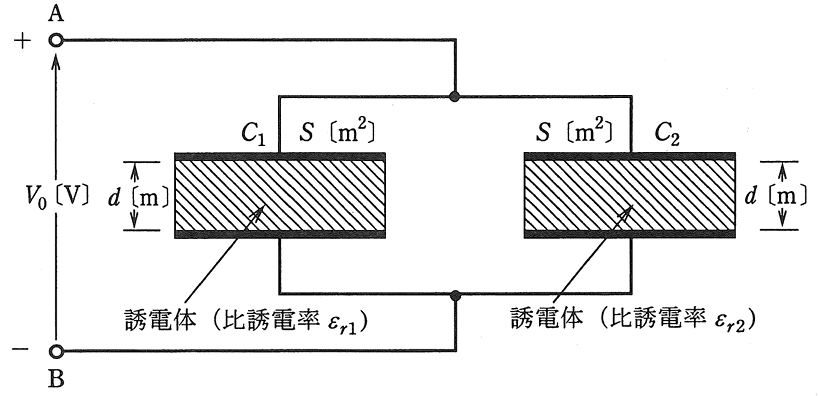
電極板面積と電極板間隔が共に\(S [m^2] \)と\(d[m] \)で、一方は比誘電率が\(ε_{r1} \)の誘電体からなる平行平板コンデンサ\(C_1\)と、他方は比誘電率が\(ε_{r2} \)の誘電体からなる平行平板コンデンサ\(C_2\)がある。
いま、これらを図のように並列に接続し、端子Ａ、Ｂ間に直流電圧\(V_0[V] \)を加えた。
このとき、コンデンサ\(C_1\)の電極板間の電界の強さを \(E_1 [V/m] \)、電束密度を \(D_1[C/m^2] \)、また、コンデンサ\(C_2\)の電極板間の電界の強さを\(E_2 [V/m] \)、電束密度を \(D_2[C/m^2] \)とする。
両コンデンサの電界の強さ\(E_1 [V/m] \)と\(E_1 [V/m] \)はそれぞれ ア であり、電束密度\(D_1[C/m^2] \)と\(D_2[C/m^2] \)はそれぞれ イ である。
したがって、コンデンサ\(C_1\)に蓄えられる電荷を\(Q_1[C] \)、コンデンサ\(C_2\)に蓄えられる電荷を\(Q_2[C] \)とすると、それらはそれぞれ ウ となる。
ただし、電極板の厚さ及びコンデンサの端効果は、無視できるものとする。
また、真空の誘電率を\(ε_0[F/m]\)とする。
上記の記述中の空白箇所（ア）、（イ）及び（ウ）に当てはまる式として、正しいものを組合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | \(\displaystyle E_1=\frac{ε_{r1}}{d}V_0\) \(\displaystyle E_2=\frac{ε_{r2}}{d}V_0\) | \(\displaystyle D_1=\frac{ε_{r1}}{d}SV_0\) \(\displaystyle D_2=\frac{ε_{r2}}{d}SV_0\) | \(\displaystyle Q_1=\frac{ε_0 ε_{r1}}{d}SV_0\) \(\displaystyle Q_2=\frac{ε_0 ε_{r2}}{d}SV_0\) |
| (2) | \(\displaystyle E_1=\frac{ε_{r1}}{d}V_0\) \(\displaystyle E_2=\frac{ε_{r2}}{d}V_0\) | \(\displaystyle D_1=\frac{ε_0 ε_{r1}}{d}V_0\) \(\displaystyle D_2=\frac{ε_0 ε_{r2}}{d}V_0\) | \(\displaystyle Q_1=\frac{ε_0 ε_{r1}}{d}SV_0\) \(\displaystyle Q_2=\frac{ε_0 ε_{r2}}{d}SV_0\) |
| (3) | \(\displaystyle E_1=\frac{V_0}{d}\) \(\displaystyle E_2=\frac{V_0}{d}\) | \(\displaystyle D_1=\frac{ε_0 ε_{r1}}{d}SV_0\) \(\displaystyle D_2=\frac{ε_0 ε_{r2}}{d}SV_0\) | \(\displaystyle Q_1=\frac{ε_0 ε_{r1}}{d}V_0\) \(\displaystyle Q_2=\frac{ε_0 ε_{r2}}{d}V_0\) |
| (4) | \(\displaystyle E_1=\frac{V_0}{d}\) \(\displaystyle E_2=\frac{V_0}{d}\) | \(\displaystyle D_1=\frac{ε_0 ε_{r1}}{d}V_0\) \(\displaystyle D_2=\frac{ε_0 ε_{r2}}{d}V_0\) | \(\displaystyle Q_1=\frac{ε_0 ε_{r1}}{d}SV_0\) \(\displaystyle Q_2=\frac{ε_0 ε_{r2}}{d}SV_0\) |
| (5) | \(\displaystyle E_1=\frac{ε_0 ε_{r1}}{d}SV_0\) \(\displaystyle E_2=\frac{ε_0 ε_{r2}}{d}SV_0\) | \(\displaystyle D_1=\frac{ε_0 ε_{r1}}{d}V_0\) \(\displaystyle D_2=\frac{ε_0 ε_{r2}}{d}V_0\) | \(\displaystyle Q_1=\frac{ε_0}{d}SV_0\) \(\displaystyle Q_2=\frac{ε_0}{d}SV_0\) |
回答
答え
(4)
回答方針
平行平板コンデンサに関する公式の理解が重要な問題です。
関係公式の項目に、書き出しました。
回答する際は、必要な関係公式を書き出してから、問題に当てはめるように進めることをお勧めします。
要点整理
コンデンサにおける関係公式を書き出して要点整理します。
- \(\displaystyle V=E d\)
平行平板コンデンサにおける電圧 \(\displaystyle V [V] \)、電界の強さ \(\displaystyle E [V/m] \)と、コンデンサ極板間距離\(\displaystyle d [m] \)の関係式です。
式を変換すると、\(\displaystyle E=\frac{V}{d}\) となります。
- \(\displaystyle D=ε E\)
平行平板コンデンサの電束密度 \(\displaystyle D [C/m^2] \)、電界の強さ \(\displaystyle E [V/m] \)と、誘電率 \(\displaystyle ε [F/m] \)の関係式です。
- \(\displaystyle Q=C V\)
コンデンサに蓄えられる電荷 \(\displaystyle Q [C]\)、静電容量 \(\displaystyle C [F] \)、電圧 \(\displaystyle V [V] \)の関係式です。
- \(\displaystyle C=ε \frac{S}{d} \)
コンデンサに蓄えられる電荷 \(\displaystyle Q [C]\)、誘電率 \(\displaystyle ε [F/m] \)、コンデンサの極板面積誘電率 \(\displaystyle S [m^2] \)と、\(\displaystyle d [m] \) の関係式です。
- \(\displaystyle ε=ε_r ε_0 \)
コンデンサの誘電率 \(\displaystyle ε [F/m] \)、比誘電率 \(\displaystyle ε_r \)と、真空の誘電率 \(\displaystyle ε_0 [F/m] \)の関係式です。
関係公式の適用
書き出した関係公式を、各回答に適用します。
ア
コンデンサの電界の強さ\(\displaystyle E_1[V/m] , E_2[V/m] \)を求める問題であるため、
書き出した関係公式1. \(\displaystyle V=E d\) を変形させて、\(\displaystyle E=\frac{V}{d}\)とすると、 両コンデンサの印加電圧は\(\displaystyle V_0\) 、両コンデンサ極板間距離\(\displaystyle d\)であることから、
\(\displaystyle E_1=\frac{V_0}{d}\)
\(\displaystyle E_2=\frac{V_0}{d}\)
と、求まります。
イ
平行平板コンデンサの電束密度 \(\displaystyle D [C/m^2] \)を求める問題であるため、書き出した関係公式2. \(\displaystyle D=ε E\) と、 ア の回答から
\(\displaystyle D_1=ε E_1=\frac{ε_0 ε_{r1}}{d}V_0\)
\(\displaystyle D_2=ε E_2=\frac{ε_0 ε_{r2}}{d}V_0\)
と、求まります。
ウ
コンデンサに蓄えられる電荷 \(\displaystyle Q [C]\)を求める問題であるため、書き出した関係公式
3.\(\displaystyle Q=C V\)、4.\(\displaystyle C=ε \frac{S}{d} \)、5.\(\displaystyle ε=ε_r ε_0 \)から、
\(\displaystyle Q=C V= \frac{ε}{d} SV= \frac{ε_rε_0}{d} SV\)と変形できます。
\(\displaystyle Q_1=\frac{ε_0 ε_{r1}}{d}SV_0\)
\(\displaystyle Q_2=\frac{ε_0 ε_{r2}}{d}SV_0\)
と求まります。
出典元
平成２１年度第三種電気主任技術者試験 理論科目Ａ問題問１
参考書
本ブログの管理人は、電験３種過去問マスタを使って電験３種を取りました。
とても解説が分かり易い参考書なのでお勧めです。
| 電験3種過去問マスタ 理論の20年間 |  |
| 電験3種過去問マスタ 電力の20年間 | |
| 電験3種過去問マスタ 機械の20年間 | |
| 電験3種過去問マスタ 法規の15年間 | |
コメント