エミッタフォロワの概要
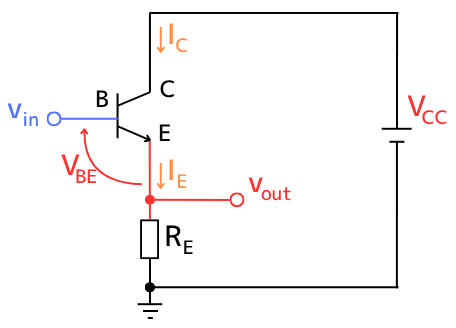
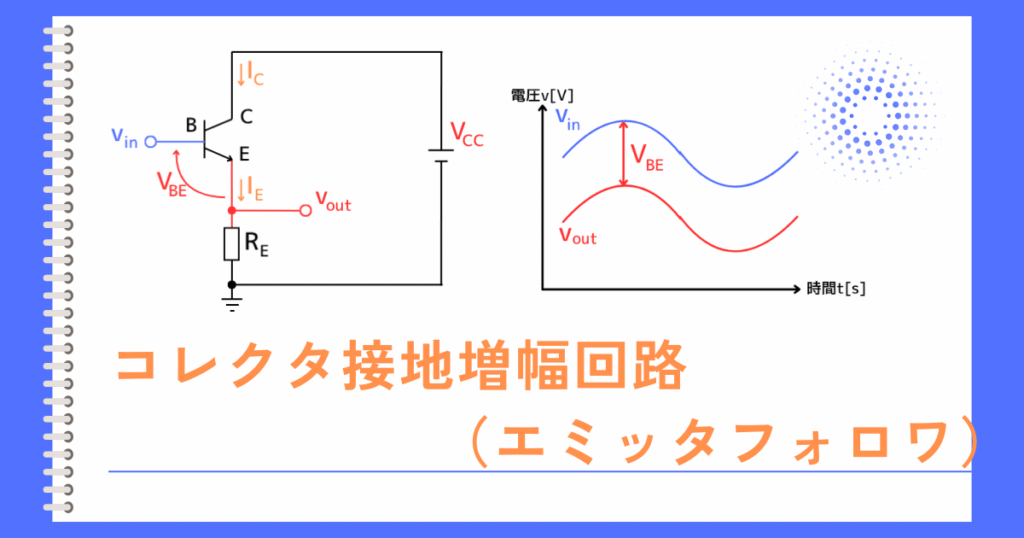
コレクタ接地増幅回路は、ベース端子に入力、エミッタ端子から出力する回路です。
コレクタ端子の電圧は、どんな信号が入力されても変動しないため、コレクタ端子は接地されていると考えられます。そのため、コレクタ接地増幅回路と呼びます。
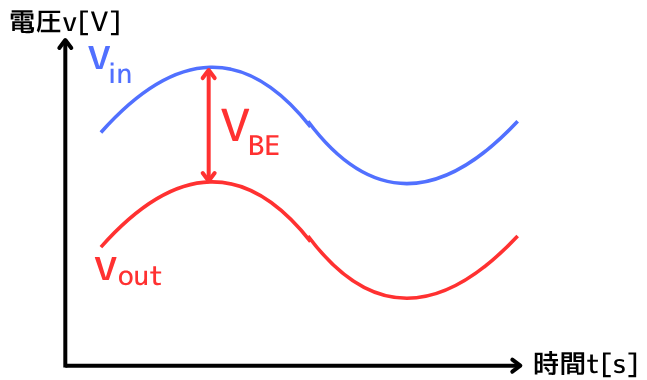
コレクタ接地増幅回路は、ベース端子への入力\(v_{in}\)に対して、ベース・エミッタ間電圧\(V_{BE}\)だけ低下した電圧が、エミッタ端子に\(v_{out}\)が出力されます。式に表すと、
\(v_{out}=v_{in}-V_{BE}\)
\(V_{BE}\)は入出力電圧が変化しても一定な電圧であるため、入力\(v_{in}\)に追従する電圧が\(v_{out}\)として出力されます。
このことから、エミッタフォロワとも呼ぶ方が一般的です。
エミッタフォロワの用途
エミッタフォロワは、入力インピーダンスが高く、出力インピーダンスが低いことからバッファ回路として使用されます。
出力インピーダンスが大きいオペアンプを、スピーカー等の低インピーダンス機器に接続すると、インピーダンスの不整合の問題で信号を上手く伝えることが出来ないため、動作させることが出来ません。
そこで、出力インピーダンスが低いバッファ回路をオペアンプの出力回路として使用することで、インピーダンスの問題をクリアし、スピーカー等の低インピーダンス負荷も動作させることができるようになります。
オペアンプ内で、電圧信号を増幅させる回路は、エミッタ接地増幅回路です。
エミッタ接地増幅回路の出力インピーダンスは大きいですが、エミッタフォロワの入力インピーダンスが大きいことから、バッファ回路は電圧信号増幅回路から送られてきた信号を、ほとんど減衰させることなく出力することが出来ます。
エミッタフォロワの特徴
長所
・入力インピーダンスが高い
・出力インピーダンスが低い
・電流増幅率が高い
・高周波特性が良い
その他の特徴
・電圧増幅度が1
・入出力位相が同相
エミッタフォロワの特性の解析
電圧増幅率\(A_v≒1\)
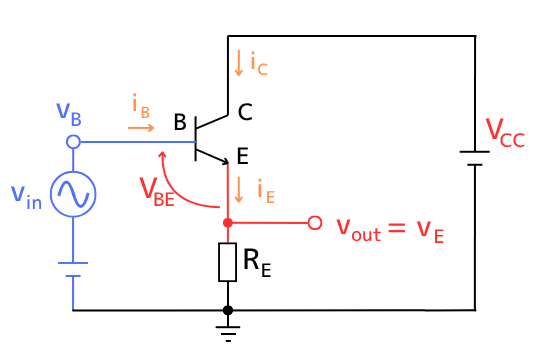
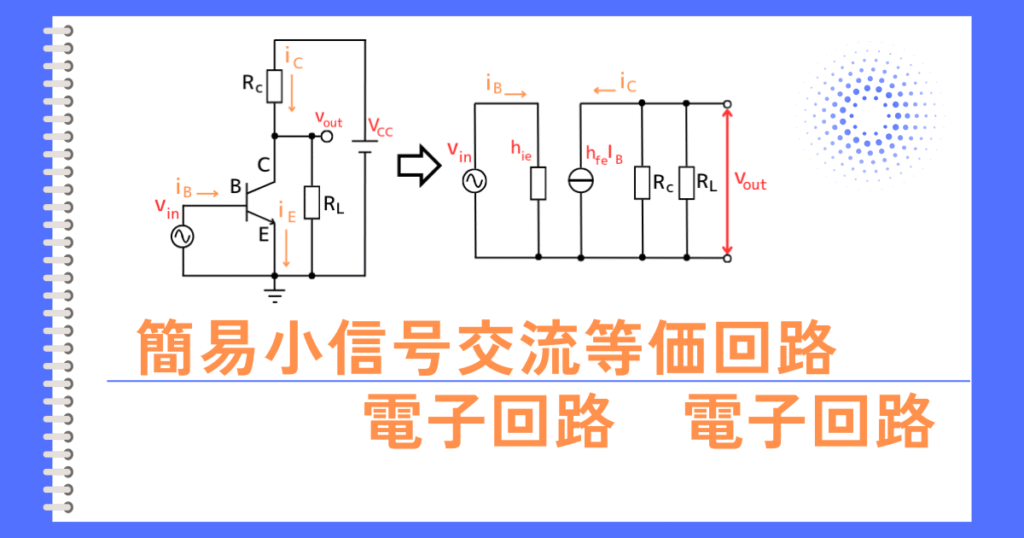
図1 エミッタフォロワ回路
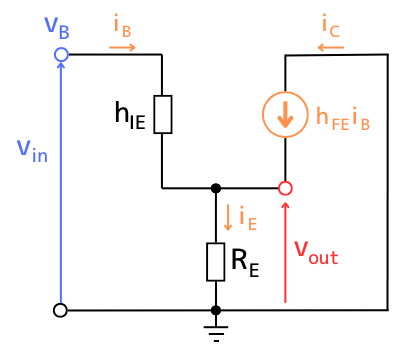
図2エミッタフォロワの簡易等価回路
コレクタ電流:\(i_C=h_{FE}i_B\)
エミッタ電流:\(i_E=i_B+i_C=(1+h_{FE})i_B\)
入力電圧:\(v_{in}=v_B=h_{IE}i_B+R_Ei_E=h_{IE}i_B+R_E(1+h_{FE})i_B\)
出力電圧:\(v_{out}=R_E(1+h_{FE})i_B\)
電圧増幅率:\(\displaystyle A_v=\frac{v_{out}}{v_{in}}=\frac{R_E(1+h_{FE})}{h_{IE}+R_E(1+h_{FE})}\)
ここで、\(R_E(1+h_{FE}) >> h_{IE}\)なので、
\(\displaystyle A_v≒1\)と簡素化できます。
入力インピーダンス

図1 エミッタフォロワ回路

図2エミッタフォロワの簡易等価回路
入力インピーダンス\(Z_{in}\)は入力電圧\(v_{in}\)に対する入力電流\(i_{in}\)の比です。
\(\displaystyle Z_{in}=\frac{v_{in}}{i_{in}}\)
入力電圧:\(v_{in}=v_B=h_{IE}i_B+R_Ei_E=h_{IE}i_B+R_E(1+h_{FE})i_B\)
入力電流:\(i_{in}=i_B\)
入力インピーダンス\(Z_{in}\)の式に代入すると、
\(\displaystyle \begin{eqnarray}
Z_{in}&=&\frac{v_{in}}{i_{in}}\\ \\
&=&h_{IE}+R_E(1+h_{FE})
\end{eqnarray}\)
【例】
\(h_{IE}=5kΩ\)、\(h_{FE}=200\)、\(R_E=1kΩ\)とした場合、
\(Z_{in}=206kΩ\)となり、高い入力インピーダンスを得られます。
出力インピーダンス
テブナンの定理から出力インピーダンスは求められます。
テブナンの定理の復習
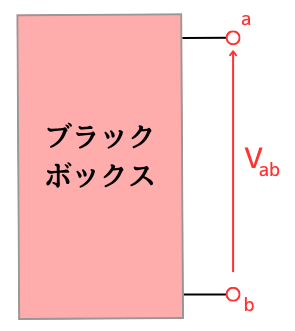
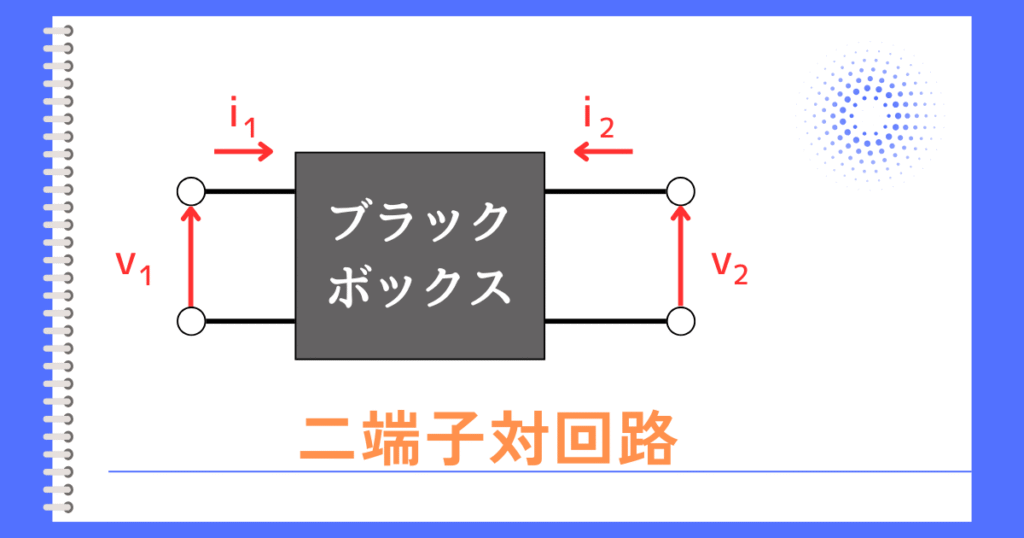
ブラックボックスの回路のa、b二つの端子を開放した時の電圧を\(V_{ab}\)とします。
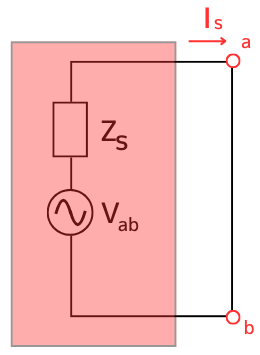
a、bの端子間を短絡した時の電流を\(I_s\)とします。
このとき、ブラックボックス内のインピーダンスは
\(\displaystyle Z_s=\frac{V_{ab}}{I_s}\)
となります。

赤で塗った範囲は、テブナン等価回路のブラックボックス部分です。
\(v_{out}\)端子は開放とします。
このときの出力電圧\(v_{out}\)は、電圧増幅率\(A_v≒1\)なので、
\(v_{out}=A_vv_{in}≒v_{in}\) …①
となります。
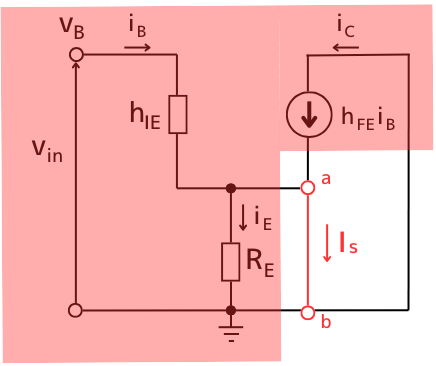
次に、端子間を短絡したとき、\(i_s\)が流れます。
\(i_s\)は、コレクタ電流\(i_C\)と、ベース電流\(i_B\)が合流して流れる電流なので、
\(i_s=i_B+i_C=(1+h_{FE})i_B\) …②
流れるベース電流\(i_B\)は、\(h_{IE}\)しかインピーダンスを通らないので、
\(\displaystyle i_B=\frac{v_{in}}{h_{IE}}\) …③
③式を②式に代入すると、
\(\displaystyle i_s=(1+h_{FE}) \frac{v_{in}}{h_{IE}}\) …④
ブラックボックス内のインピーダンスは
\(\displaystyle \begin{eqnarray}
Z_s&=&\frac{v_{out}}{i_s}\\ \\
&=&\frac{v_{in}}{(1+h_{FE}) \frac{v_{in}}{h_{IE}}}\\ \\
&=&\frac{h_{IE}}{1+h_{FE}}
\end{eqnarray}\)
【例】
\(h_{IE}=5kΩ\)、\(h_{FE}=200\)、とした場合、
\(\displaystyle Z_s=\frac{h_{IE}}{1+h_{FE}}=\frac{5000}{1+200}=24.9Ω\)となり、低い出力インピーダンスを得られます。
【余談】
電験三種には不要な知識ですが、スピーカーのインピーダンスは\(4Ω\)、\(8Ω\)程度のため、エミッタフォロワだけでは十分な低出力インピーダンスは得られません。
スピーカーのような低インピーダンス負荷を駆動する場合は、もっと高い\(h_{FE}\)を得られるダーリントン接続を使用する等の工夫が必要です。
電流増幅率

入力電流は\(i_{in}=i_B\)です。
出力電流は\(i_{out}=i_E\)です。
\(i_E=i_B+i_C=(1+h_{FE})i_B\)
電流増幅率\(A_i\)は、
\(A_i=\frac{i_{out}}{i_{in}}=1+h_{FE}\)
となり、高い電流増幅率を得られます。
【例】
\(h_{FE}=200\)、とした場合、\(A_i=1+h_{FE}=201\)となります。
周波数特性
入力が印加されるベース電圧\(v_B\)、出力信号を得られるエミッタ電圧\(v_E\)と、ベースエミッタ間電圧\(V_{BE}\)の関係は、
\(v_E=v_B-V_{BE}\)
です。\(V_{BE}\)はほぼ固定値であることから、同位相で同振幅で電圧が変化します。
このことから、ベースエミッタ間に寄生容量\(C_{BE}\)が存在していても、見かけ上\(C_{BE}=0\)となります。
そのため、高い周波数帯域でも信号が減衰しない特性を得られます。
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント