電気力線の性質
電気力線とは
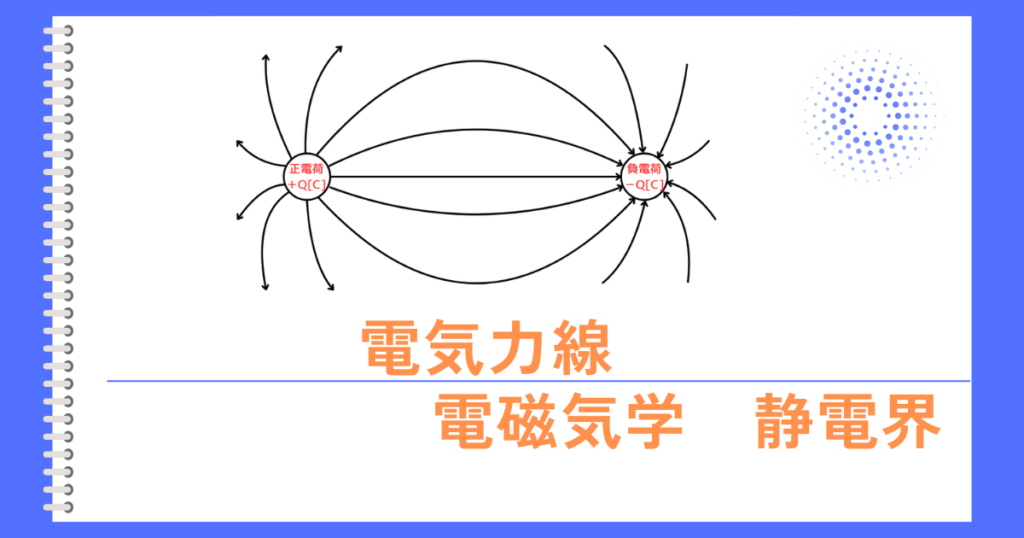
電気力線とは、電荷が作り出す電界の向きを視覚的に表現するために使われる仮想的な線です。
正の点電荷からは放射状に電気力線が放出され、負の点電荷に電気力線が吸収されます。
電気力線の性質
電気力線には様々な重要な性質がありますので、それを列挙します。
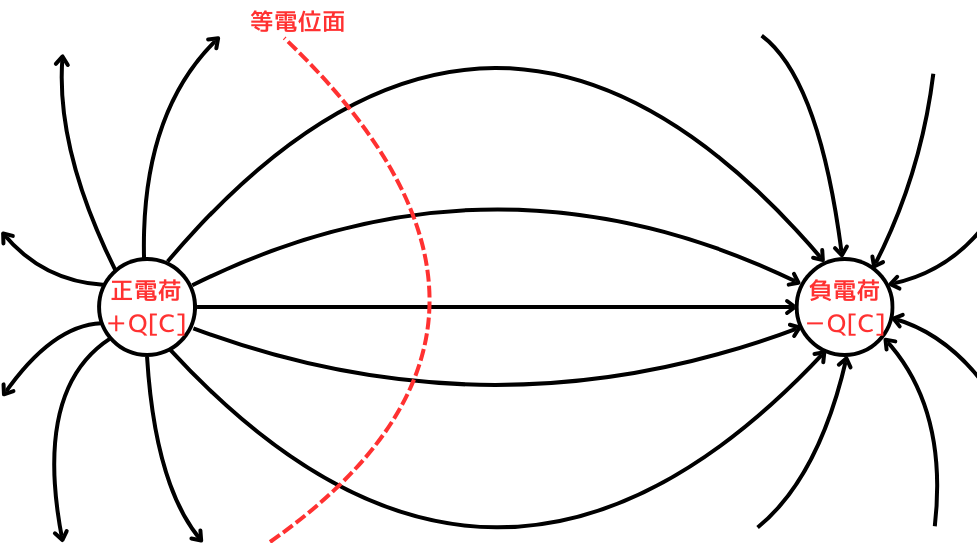
電気力線の性質
・+電荷から出て、-電荷に入る
・電荷の無い所からは発生も消失も
しない
・電気力線は交わらない
・電気力線は枝分かれしない
・電気力線は途切れない
・電気力線と等電位面は直交する
・電界の方向は電気力線の接線方向
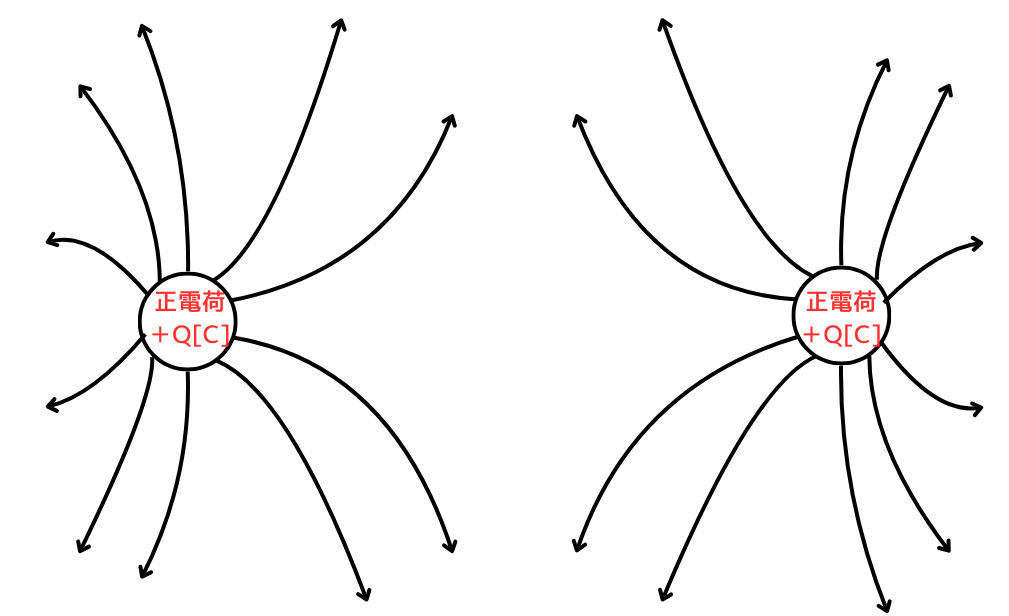
電気力線の性質(続き)
・正電荷同士もしくは負電荷同士の
同じ符号の電荷を近づけた場合、
電気力線は交わらず、反発しあう。
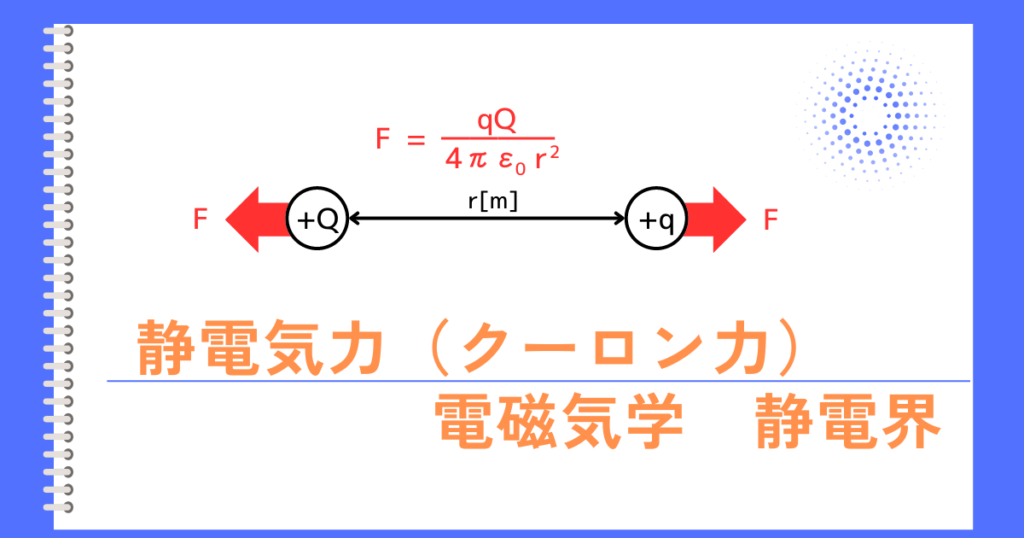
電束\(Q\)と電気力線の本数\(N\)[本]
\(Q[C]\)の電荷から出る電束は、\(Q[C]\)です。
つまり、電荷量=電束です。
\(Q[C]\)の電荷から出る電気力線の本数N[本]は、\(\displaystyle N=\frac{Q}{ε_0}\)です。
\(Q[C]\)の電束の密度は、電束密度\(D[C/m^2]\)です。
\(N\)[本]の電気力線の密度は、電界強度\(E[V/m]\)です。
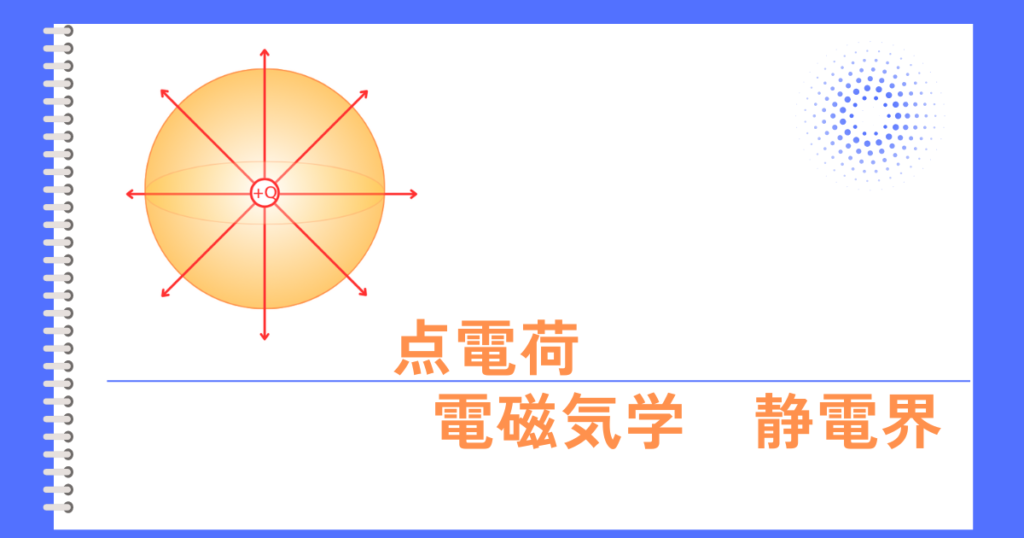
電束\(Q[C]\)の広がりと、\(N\)[本]の電気力線の広がりのイメージ
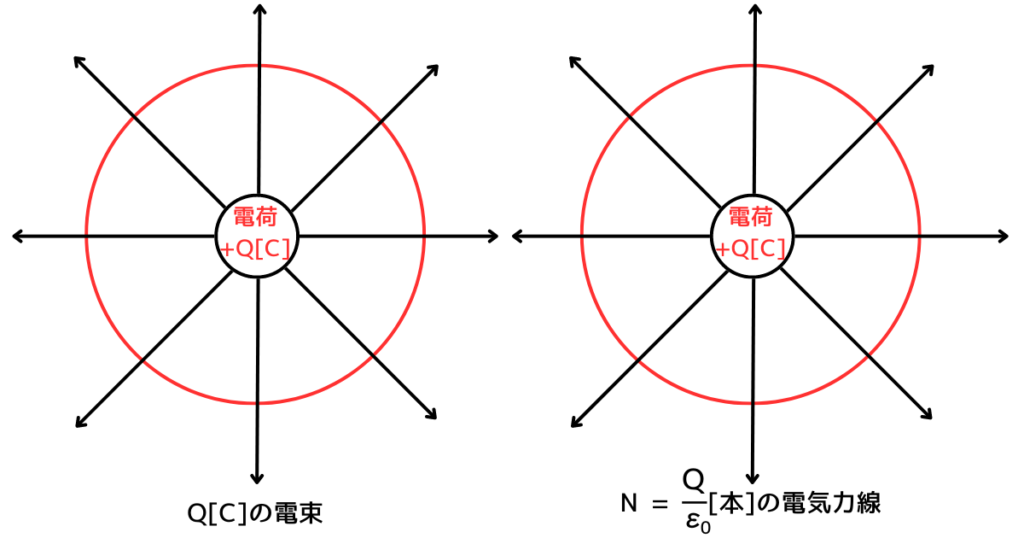
電束も、電気力線も、電荷から放射状に広がります。
電気力線の本数N[本]の式の意味
\(\displaystyle N=\frac{Q}{ε_0}\) …①
この①式は、便宜的に決めた式であり、①式自体に深い意味はありません。
では、便宜的とは何か。それは、ガウスの法則の式において、
\(\displaystyle \oint_S EdS=\frac{Q}{ε_0}\) …②
②式の右辺に便宜的に決めた①式を代入すると、次のように簡略化できるためです。
\(\displaystyle \oint_S EdS=N\) …③
次に、積分の形だとわずらわしいので、
\(\oint_S EdS=ES\)
と展開すると、③式は次のように変形できます。
\(ES=N\) ⇒ \(\displaystyle E=\frac{N}{S}\)
この式から、電界強度\(E[V/m]\)は、電気力線の本数\(N\)[本]の密度であると言えます。
過去問
難易度 ★☆☆☆☆
電験三種 令和2年度 問2
電験三種 令和4年度下期 問1
電験三種 令和5年度上期 問2
難易度 ★★☆☆☆
電験三種 令和4年度下期 問2
関連記事(静電界に関する解説)
参考書
単位が取れる電磁気学シリーズは、電磁気学に関して根本的に理解を深めたい人に最もお勧めな参考書です。電磁気学で詰まりやすい大学生のバイブル的な一冊で、体系的な理解をすることができます。
電磁気ノートは、電験三種に必要な内容から、電験一種の内容まで全て入っています。
全て読破しようとすると、学習すべき範囲に対して過剰になるので、過去問のわからない箇所があったら、単位が取れる電磁気ノートで調べるという使用方法がお勧め。
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。



コメント