概要
高校で学んだ基礎物理学の復習です。
運動方程式と、等加速度直線運動について解説します。
公式一覧
質量\(m[kg]\)、働く力\(F[N]\)、加速度\(α[m/s^2]\)、速度\(v[m/s]\)、位置\(x[m]\)、時間\(t[s]\)
基準時間\(t_0[s]\)、初速\(v_0[m/s]\)、初期位置\(x_0[m]\)としたとき、それぞれの関係式は次の通りです。
運動方程式
\(F=mα[N]\)
速度 \(v[m/s]\)
\(v=αt+v_0\)
ただし、初速\(v_0=0[m/s]\)のとき、
\(v=αt\)
位置 \(x[m]\)
\(\displaystyle x=\frac{1}{2}αt^2+v_0t+x_0\)
ただし、初速\(v_0=0[m/s]\)、初期位置\(x_0=0[m]\)のとき、
\(\displaystyle x=\frac{1}{2}αt^2\)
運動方程式
運動方程式とは、質量\(m[kg]\)の物体に、力\(F[N]\)を加え続けたときに加速度\(α[m/s^2]\)が生じることを表す式です。
文字通りに立式すると、\(\displaystyle α=\frac{F}{m}\)となります。
分数形式で表現すると、mとFのどちらが分母か忘れる場合があるので、
\(F=mα\)
と、運動方程式を書き出した方が一般的でしょう。
自由落下の場合
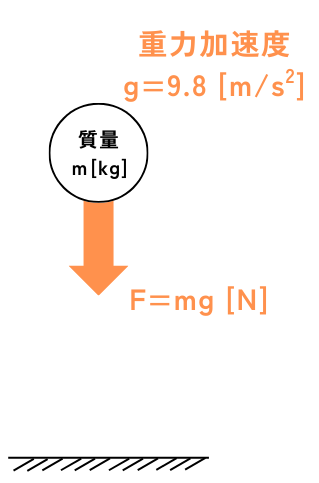
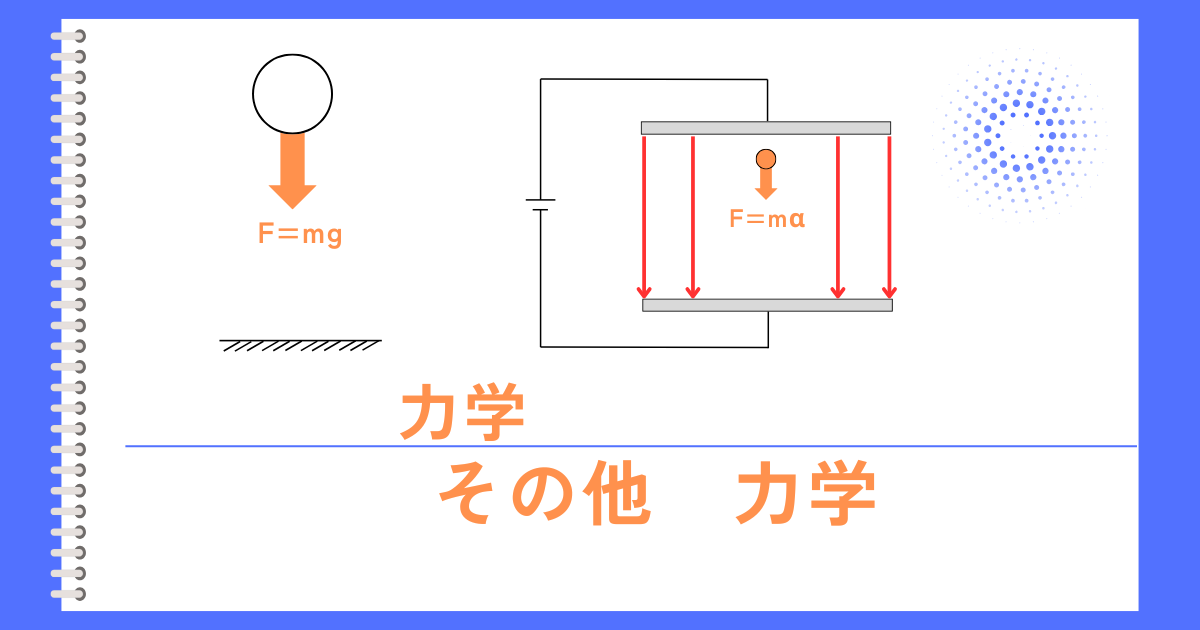
質量\(m[kg]\)の物を持ち上げてから手を放すと、その物は落ちます。
これを自由落下と呼び、その加速度\(α[m/s^2]\)は重力加速度\(g=9.8[m/s^2]\)で一定となり、その運動方程式は次式となります。
\(F=mg[N]\)
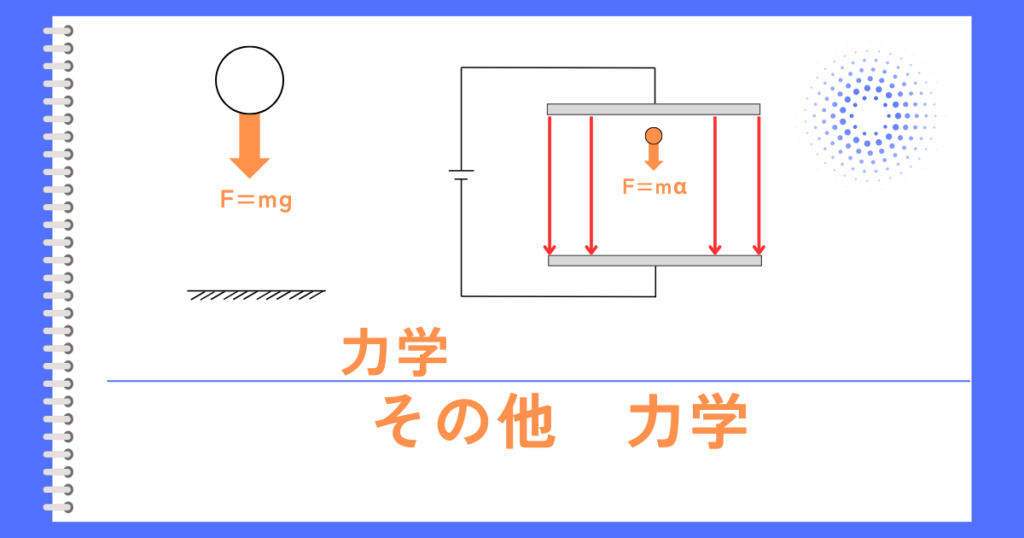
質量\(m[kg]\)の電荷に静電気力\(F=qE\)が働く場合
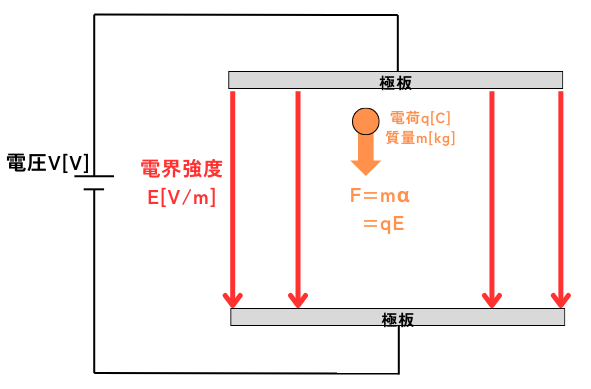
左図のように、平行平板コンデンサの間に質量\(m[kg]\)で電荷量\(q[C]\)の電荷があるとします。
そして、平行平板コンデンサには、電界強度\(E[V/m]\)の一様な電界があるとします。
この時、電荷\(q\)に、静電気力\(F=qE\)が働くときの加速度\(α\)は次の通り展開されます。
\(F=qE=mα\)
⇔ \(\displaystyle α=\frac{qE}{m}[m/s^2]\)
この式から、電荷量\(q[C]\)か電界強度\(E[V/m]\)が大きくなると、加速度も大きくなることがわかります。
等加速度直線運動
等加速度直線運動は、等加速度の文字通り、加速度\(α[m/s^2]\)が一定の運動です。
物が進む向きと加速度の向きが同じとき、直線運動します。
等加速度直線運動の代表例は、物体の自由落下(空気抵抗等は無視する)です。
加速度\(α[m/s^2]\)、速度\(v[m/s]\)、位置\(x[m]\)の関係は、微分積分で表される関係なので、それを示していきます。
\(α[m/s^2]\) ― \(v[m/s]\)の関係式
加速度\(α[m/s^2]\)は、単位時間当たりの速度\(v[m/s]\)の変化量です。
つまり、1秒で速度\(v\)がどれくらい変化したかを表します。
時間を細かく分解していくと、細かく速度の変化量が見れることから、加速度\(α\)と速度\(v\)の関係は微分で表せます。
\(\displaystyle α=\frac{dv}{dt}\)
微分とは逆に、積分で加速度\(α\)と速度\(v\)の関係を表すこともできます。
\(v=\int α dt=αt+C_1\)
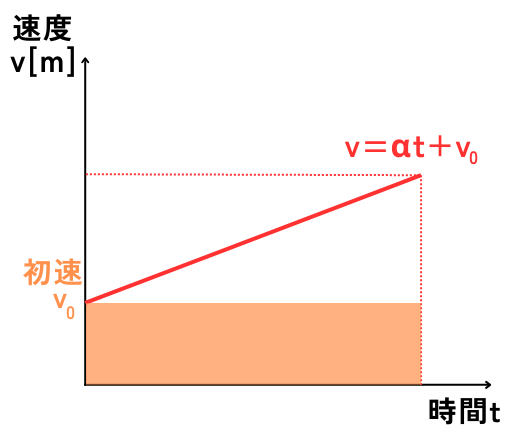
積分定数\(C_1\)は、速度\(v\)の初期値である初速\(v_0[m/s]\)を表します。
したがって、次式となります。
\(v=αt+v_0\)
\(v[m/s]\) — \(x[m]\)の関係式
速度\(v[m/s]\)は、単位時間当たりの位置\(x[m]\)の変化量です。
つまり、1秒で位置\(x\)がどれくらい変化したかを表します。
時間を細かく分解していくと、細かく速度の変化量が見れることから、速度\(v\)と位置\(x\)の関係は微分で表せます。
\(\displaystyle v=\frac{dx}{dt}\)
微分とは逆に、積分で速度\(v\)と位置\(x\)の関係を表すこともできます。
\(x=\int v dt\)
速度は、\(v=αt+v_0\)で表されるので、
\(\displaystyle x=\int αt+v_0 dt=\frac{1}{2}αt^2+v_0t+C_2\)
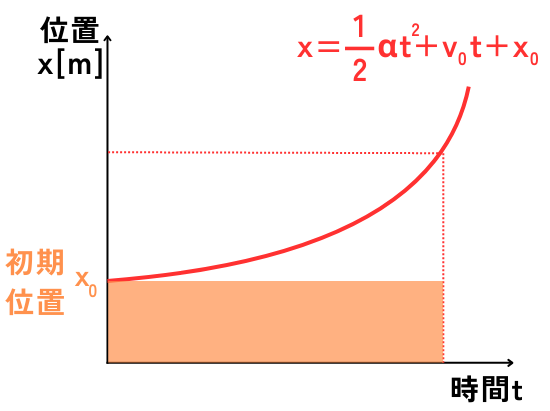
積分定数\(C_2\)は、位置\(x\)の初期値である初期位置\(x_0[m/s]\)を表します。
したがって、次式となります。
\(\displaystyle x=\frac{1}{2}αt^2+v_0t+x_0\)
関連記事(その他)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント