概要
三相交流の負荷の結線にはΔ(デルタ)結線と、Y(スター)結線があります。
負荷電流や電力の解析をする際に、Δ結線だと解析しづらい場合、Y結線だと解析しづらい場合があります。
Δ結線とY結線は、それぞれ等価変換をすると解析しやすくなります。この等価変換の方法を次のように呼び分けることとします。
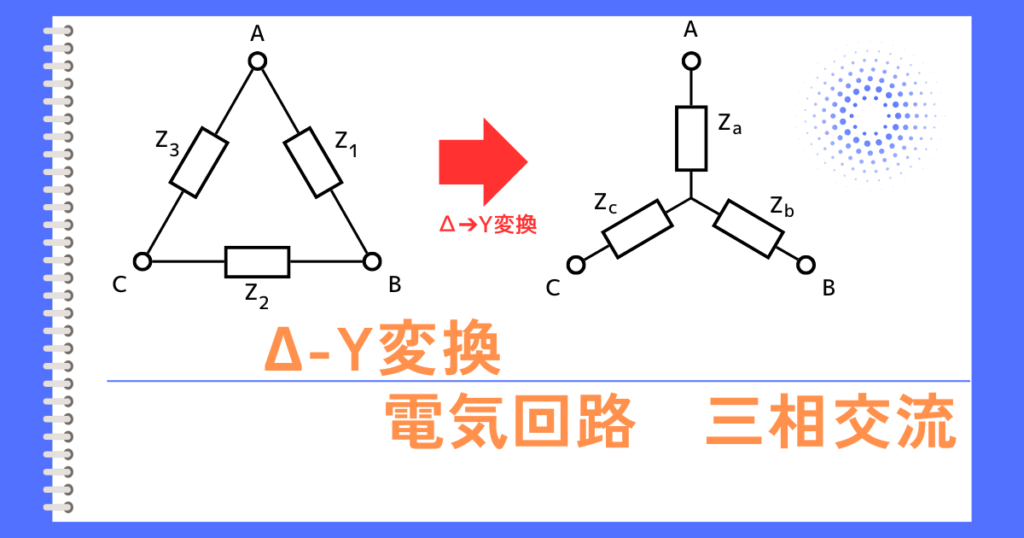
・Δ結線➔Y結線に変換するのを、Δ-Y変換
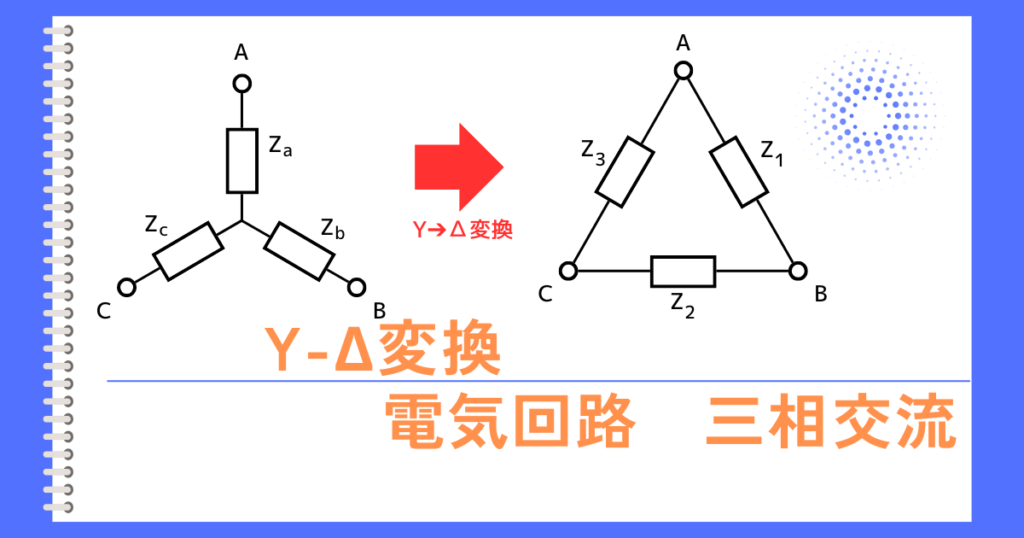
・Y結線➔Δ結線に変換するのを、Y-Δ変換
本ページでは、Δ-Y変換について解説します。
重要公式
Δ-Y変換
三相不平衡負荷の時(3相の負荷の大きさが異なるとき)
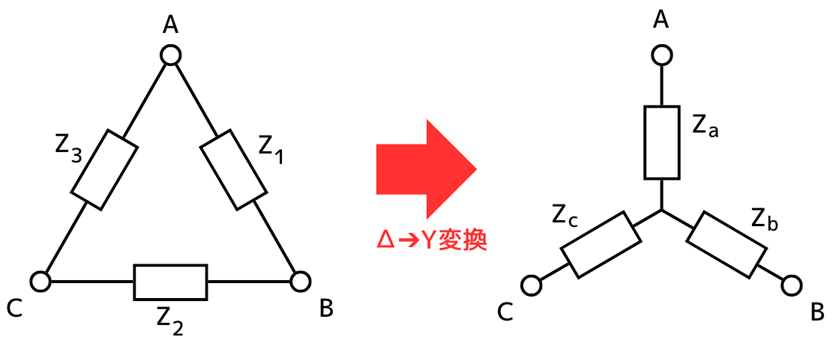
\(\displaystyle Z_a=\frac{Z_3Z_1}{Z_1+Z_2+Z_3}[Ω]\)
\(\displaystyle Z_b=\frac{Z_1Z_2}{Z_1+Z_2+Z_3}[Ω]\)
\(\displaystyle Z_c=\frac{Z_2Z_3}{Z_1+Z_2+Z_3}[Ω]\)
三相平衡負荷の時(3相の負荷の大きさが同じとき)
\(Z_Δ=Z_1=Z_2=Z_3\)
\(\displaystyle Z_Y=Z_a=Z_b=Z_c\)
としたとき、この二つのインピーダンスの関係は、
\(Z_Δ=3Z_Y\)
証明
証明の流れ
①Δ結線の端子A-B間の合成抵抗\(Z_{AB}\)を求める …(1)式
②Δ結線の端子B-C間の合成抵抗\(Z_{BC}\)を求める …(2)式
③Δ結線の端子C-A間の合成抵抗\(Z_{CA}\)を求める …(3)式
④Y結線の端子A-B間の合成抵抗\(Z_{AB}\)を求める …(4)式
⑤Y結線の端子B-C間の合成抵抗\(Z_{BC}\)を求める …(5)式
⑥Y結線の端子C-A間の合成抵抗\(Z_{CA}\)を求める …(6)式
⑦(1)式=(4)式 …(7)式
⑧(2)式=(5)式 …(8)式
⑨(3)式=(6)式 …(9)式
⑩(7)式+(8)式+(9)式を求める …(10)式
⑪(10)式-(8)式 から、Y結線の抵抗\(Z_a\)を求める
⑫(10)式-(9)式 から、Y結線の抵抗\(Z_b\)を求める
⑬(10)式-(7)式 から、Y結線の抵抗\(Z_c\)を求める
①Δ結線の端子A-B間の合成インピーダンス\(Z_{AB}\)を求める …(1)式
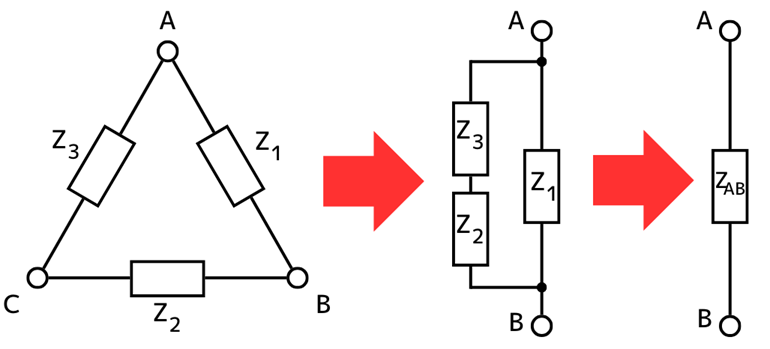
左図から、端子A-B間からみた合成インピーダンス\(Z_{AB}\)を求めます。
\(\displaystyle \frac{1}{Z_{AB}}=\frac{1}{Z_1}+\frac{1}{Z_2+Z_3}\)
整理すると、
\(\displaystyle Z_{AB}=\frac{Z_1Z_2+Z_3Z_1}{Z_1+Z_2+Z_3}\) …(1)式
②Δ結線の端子B-C間の合成インピーダンス\(Z_{BC}\)を求める …(2)式
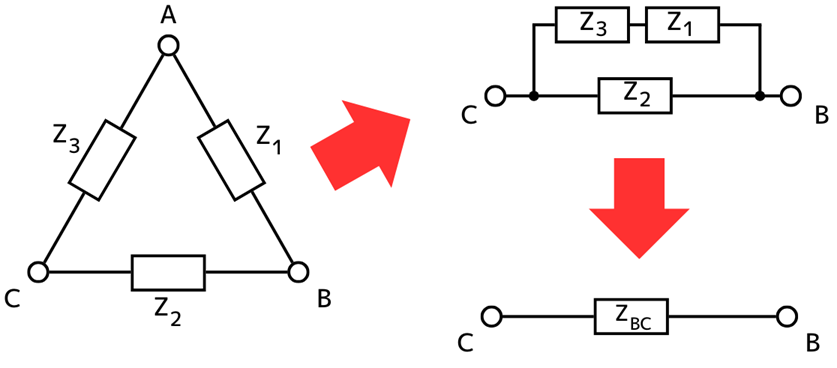
左図から、端子B-C間からみた合成インピーダンス\(Z_{BC}\)を求めます。
\(\displaystyle \frac{1}{Z_{BC}}=\frac{1}{Z_2}+\frac{1}{Z_1+Z_3}\)
整理すると、
\(\displaystyle Z_{BC}=\frac{Z_1Z_2+Z_2Z_3}{Z_1+Z_2+Z_3}\) …(2)式
③Δ結線の端子C-A間の合成インピーダンス\(Z_{CA}\)を求める …(3)式
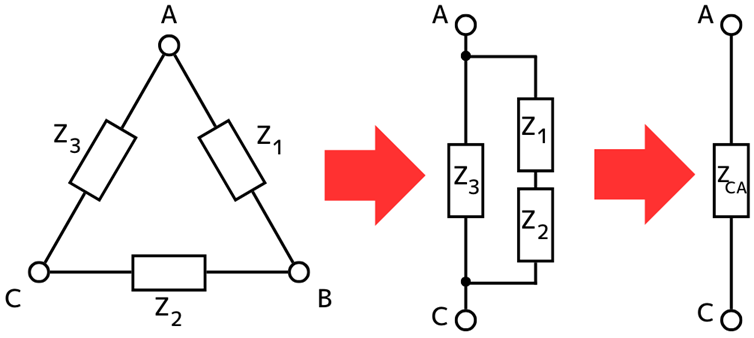
左図から、端子C-A間からみた合成インピーダンス\(Z_{CA}\)を求めます。
\(\displaystyle \frac{1}{Z_{CA}}=\frac{1}{Z_3}+\frac{1}{Z_1+Z_2}\)
整理すると、
\(\displaystyle Z_{CA}=\frac{Z_2Z_3+Z_3Z_1}{Z_1+Z_2+Z_3}\) …(3)式
④Y結線の端子A-B間の合成インピーダンス\(Z_{AB}\)を求める …(4)式
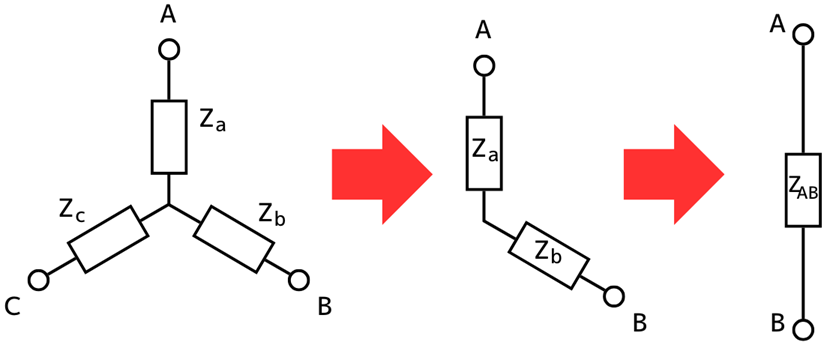
左図から、端子A-B間からみた合成インピーダンス\(Z_{AB}\)を求めます。
\(Z_{AB}=Z_a+Z_b\) …(4)式
⑤Y結線の端子B-C間の合成インピーダンス\(Z_{BC}\)を求める …(5)式
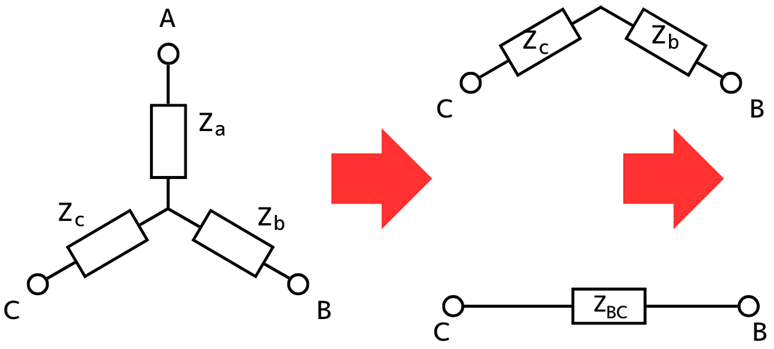
左図から、端子B-C間からみた合成インピーダンス\(Z_{BC}\)を求めます。
\(Z_{BC}=Z_b+Z_c\) …(5)式
⑥Y結線の端子C-A間の合成インピーダンス\(Z_{CA}\)を求める …(6)式
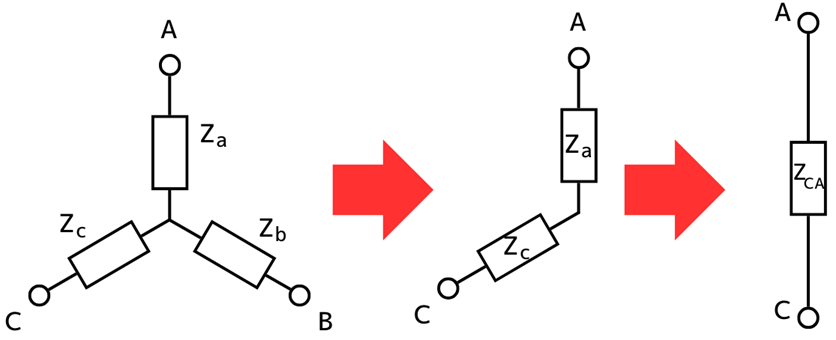
左図から、端子C-A間からみた合成インピーダンス\(Z_{CA}\)を求めます。
\(Z_{CA}=Z_c+Z_a\) …(6)式
⑦(1)式=(4)式 …(7)式
Δ結線の(1)式、Y結線の(4)式は共に\(Z_{AB}\)なので、(1)式=(4)式として式をつなげます。
\(\displaystyle Z_a+Z_b=\frac{Z_1Z_2+Z_3Z_1}{Z_1+Z_2+Z_3}\) …(7)式
⑧(2)式=(5)式 …(8)式
Δ結線の(2)式、Y結線の(5)式は共に\(Z_{BC}\)なので、(2)式=(5)式として式をつなげます。
\(\displaystyle Z_b+Z_c=\frac{Z_1Z_2+Z_2Z_3}{Z_1+Z_2+Z_3}\) …(8)式
⑨(3)式=(6)式 …(9)式
Δ結線の(3)式、Y結線の(6)式は共に\(Z_{CA}\)なので、(3)式=(6)式として式をつなげます。
\(\displaystyle Z_b+Z_c=\frac{Z_1Z_2+Z_2Z_3}{Z_1+Z_2+Z_3}\) …(9)式
⑩(7)式+(8)式+(9)式を求める …(10)式
(7)式+(8)式+(9)式を求めます。
\(\displaystyle 2(Z_a+Z_b+Z_c)=\frac{2(Z_1Z_2+Z_2Z_3+Z_3Z_1)}{Z_1+Z_2+Z_3}\)
⇔\(\displaystyle Z_a+Z_b+Z_c=\frac{Z_1Z_2+Z_2Z_3+Z_3Z_1}{Z_1+Z_2+Z_3}\) …(10)式
⑪(10)式-(8)式 から、Y結線のインピーダンス\(Z_a\)を求める
\(\displaystyle Z_a+Z_b+Z_c-(Z_b+Z_c)=\frac{Z_1Z_2+Z_2Z_3+Z_3Z_1}{Z_1+Z_2+Z_3}-\frac{Z_1Z_2+Z_2Z_3}{Z_1+Z_2+Z_3}\)
⇔\(\displaystyle Z_a=\frac{Z_3Z_1}{Z_1+Z_2+Z_3}\)
⑫(10)式-(9)式 から、Y結線のインピーダンス\(Z_b\)を求める
\(\displaystyle Z_a+Z_b+Z_c-(Z_b+Z_c)=\frac{Z_1Z_2+Z_2Z_3+Z_3Z_1}{Z_1+Z_2+Z_3}-\frac{Z_2Z_3+Z_3Z_1}{Z_1+Z_2+Z_3}\)
⇔\(\displaystyle Z_b=\frac{Z_1Z_2}{Z_1+Z_2+Z_3}\)
⑬(10)式-(7)式 から、Y結線のインピーダンス\(Z_c\)を求める
\(\displaystyle Z_a+Z_b+Z_c-(Z_a+Z_b)=\frac{Z_1Z_2+Z_2Z_3+Z_3Z_1}{Z_1+Z_2+Z_3}-\frac{Z_1Z_2+Z_3Z_1}{Z_1+Z_2+Z_3}\)
⇔\(\displaystyle Z_c=\frac{Z_2Z_3}{Z_1+Z_2+Z_3}\)
以上より、Y結線のインピーダンス\(Z_a,Z_b,Z_c\)と、Δ結線のインピーダンス\(Z_1,Z_2,Z_3\)の関係を示すことが出来ました。
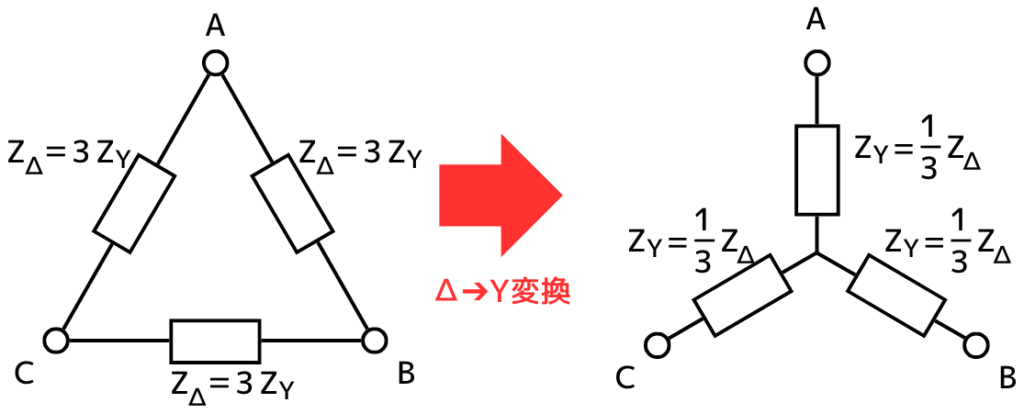
Δ-Y変換の簡易導出(三相平衡負荷の場合)
重要公式の項目で、
\(Z_Δ=Z_1=Z_2=Z_3\)
\(\displaystyle Z_Y=Z_a=Z_b=Z_c\)
としたとき、この二つのインピーダンスの関係は、\(Z_Δ=3Z_Y\)と示しました。
\(Z_Y\)が\(Z_Δ\)の3倍の大きさか、\(Z_Δ\)が\(Z_Y\)の3倍の大きさか、どちらが正しいかをふと忘れる瞬間があります。(筆者は、一々暗記していたら記憶すべき事が多くなりすぎるので、どちらが大きいか記憶していません。)
そんなふとした瞬間に、\(Z_Y\)と\(Z_Δ\)の関係性を簡単に導き出せる方法を示します。
Δ-Y変換の関係式導出手順
①Δ結線の端子A-B間の合成抵抗\(Z_{AB}\)を求める …(1)式
②Y結線の端子A-B間の合成抵抗\(Z_{AB}\)を求める …(2)式
③(1)式=(2)式 から、\(Z_Δ=3Z_Y\)を導出する
①Δ結線の端子A-B間の合成抵抗\(Z_{AB}\)を求める …(1)式
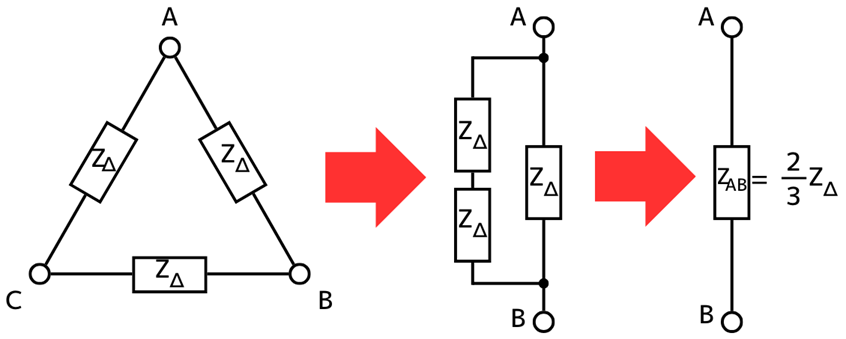
左図から、Δ結線の端子A-B間からみた合成インピーダンス\(Z_{AB}\)は、
\(\displaystyle \frac{1}{Z_{AB}}=\frac{1}{Z_Δ}+\frac{1}{2Z_Δ}\)
整理すると、
\(\displaystyle Z_{AB}=\frac{2}{3}Z_Δ\) …(1)式
②Y結線の端子A-B間の合成抵抗\(Z_{AB}\)を求める …(2)式
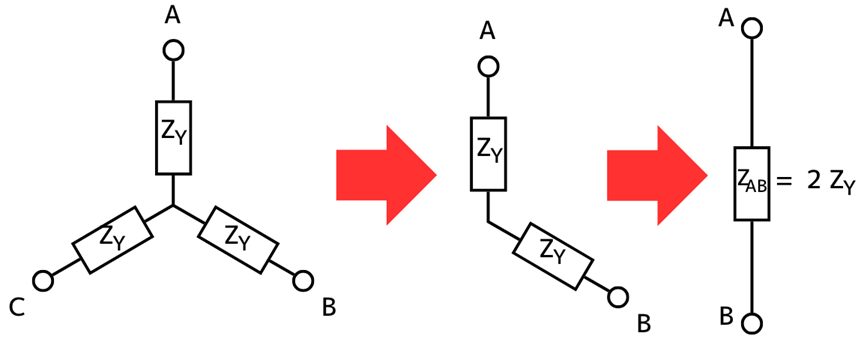
左図から、Y結線の端子A-B間からみた合成インピーダンス\(Z_{AB}\)は、
\(Z_{AB}=2Z_Y\) …(2)式
③(1)式=(2)式 から、\(Z_Δ=3Z_Y\)を導出する
(1)式=(2)式
\(\displaystyle \frac{2}{3}Z_Δ=2Z_Y\)
⇔\(\displaystyle Z_Δ=3Z_Y\)
以上より、\(Z_Δ\)と\(Z_Y\)の関係を求めることが出来ました。
コンデンサのΔ-Y変換
コンデンサの静電容量\(C[F]\)と、インピーダンス\(Z[Ω]\)の関係は、
\(\displaystyle Z=\frac{1}{jωC}\)
です。
このことから、3相のコンデンサの容量\(C[F]\)が同じとして、Δ結線の静電容量\(C_Δ[F]\)、Y結線の静電容量\(C_Y[F]\)とすると、\(Z_Δ=3Z_Y\)の関係式から、
\(\displaystyle \frac{1}{jωC_Δ}=3\frac{1}{jωC_Y}\)
⇔ \(C_Y=3C_Δ\)
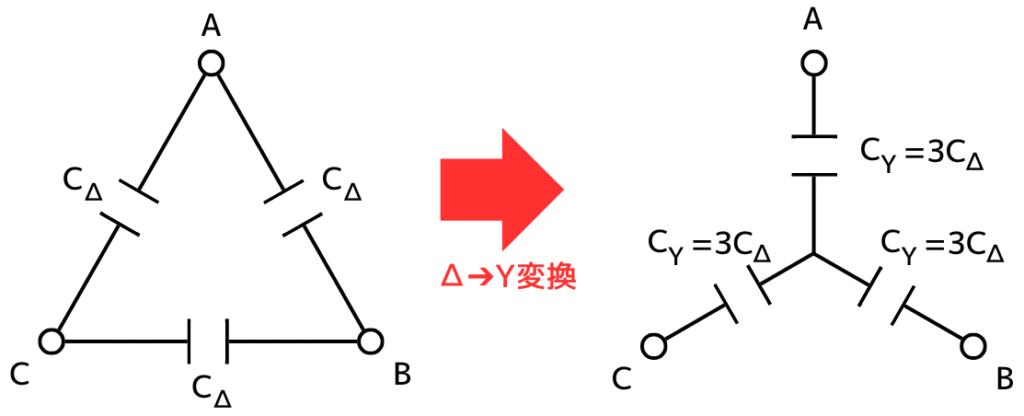
以上より、静電容量はインピーダンスに対して逆数であることから、Y結線の静電容量はΔ結線の静電容量の3倍の大きさになります。
関連記事(その他)
三相交流回路
交流回路
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。

コメント