インピーダンスの関連式 一覧
インピーダンス\(\dot{Z}[Ω]\)、抵抗\(R[Ω]\)、リアクタンス\(X[Ω]\)の関係式
\(\dot{Z}=R+jX\)
インピーダンス\(\dot{Z}[Ω]\)と、インピーダンスの大きさ\(Z\)、インピーダンスの位相\(∠θ\)の関係式
\(\dot{Z}=Z∠θ\)
インピーダンスの大きさ\(Z[Ω]\)、レジスタンス(抵抗)\(R[Ω]\)、リアクタンス\(X[Ω]\)の関係式
\(Z=\sqrt{R^2+X^2}\)
インピーダンスの位相角\(θ\)、レジスタンス(抵抗)\(R[Ω]\)、リアクタンス\(X[Ω]\)の関係式
\(tanθ=\frac{X}{R}\)
⇔ \(θ=tan^{-1}\frac{X}{R}\)
インピーダンスの加算\(\dot{Z}_{add}\)
\(\dot{Z}_{add}=(R_1+R_2)+j(X_1+X_2)\)
大きさ\(Z_{add}=\sqrt{(R_1+R_2)^2+(X_1+X_2)^2}\)
位相角\(θ_{add}=tan^{-1}\frac{X_1+X_2}{R_1+R_2}\)
インピーダンスの減算\(\dot{Z}_{sub}\)
\(\dot{Z}_{sub}=(R_1-R_2)+j(X_1-X_2)\)
大きさ\(Z_{sub}=\sqrt{(R_1-R_2)^2+(X_1-X_2)^2}\)
位相角\(θ_{sub}=tan^{-1}\frac{X_1-X_2}{R_1-R_2}\)
インピーダンスの乗算\(\dot{Z}_{mlt}\)
\(\dot{Z}_{mlt}=Z_1Z_2∠(θ_1+θ_2)\)
大きさ\(Z_{mlt}=Z_1Z_2\)
位相角\(θ_{mlt}=∠(θ_1+θ_2)\)
インピーダンスの除算\(\dot{Z}_{div}\)
\(\dot{Z}_{div}=\frac{Z_1}{Z_2}∠(θ_1-θ_2)\)
大きさ\(Z_{div}=\frac{Z_1}{Z_2}\)
位相角\(θ_{div}=∠(θ_1-θ_2)\)
虚数単位\(j\)の式
\(j=\sqrt{-1}\)
\(j^2=-1\)
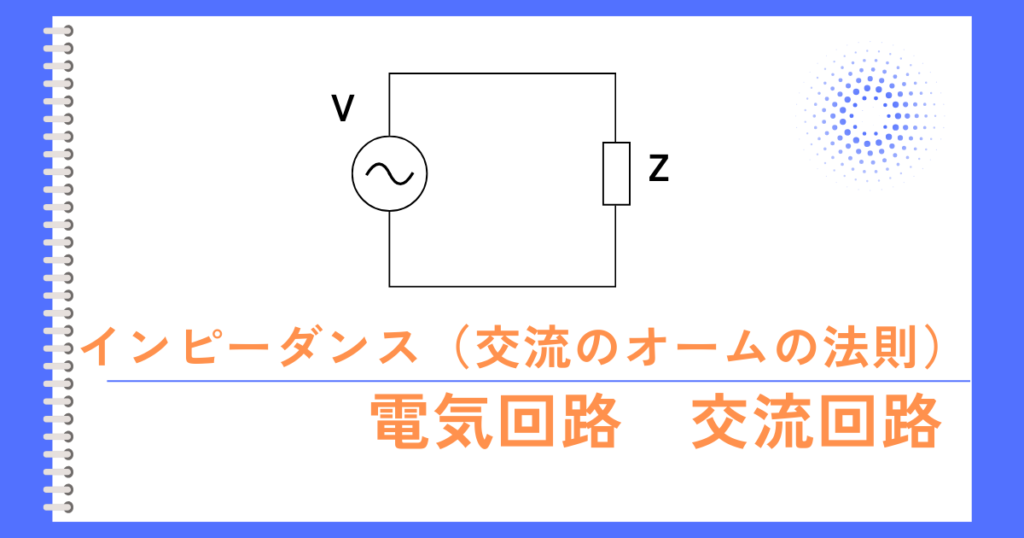
複素インピーダンス\(\dot{Z}\)
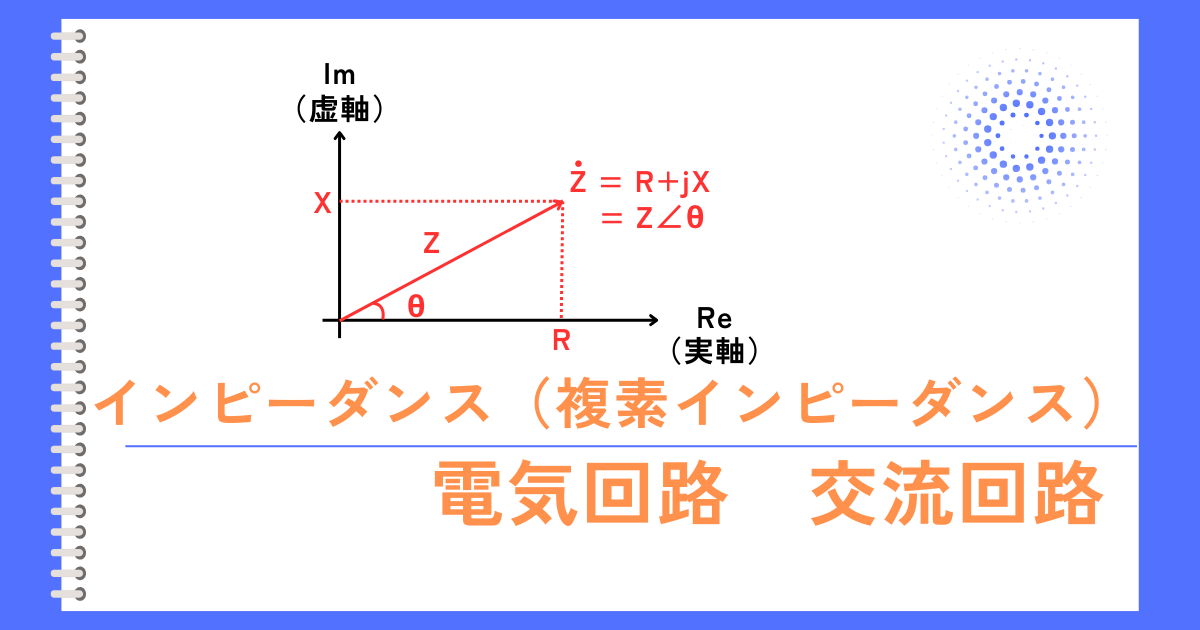
複素インピーダンス(直交座標系)
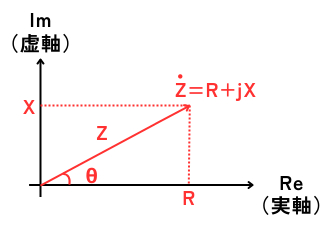
インピーダンス\(Z[Ω]\)は、電流を流れにくくする要素である抵抗\(R[Ω]\)と、リアクタンス\(X[Ω]\)を足し合わせたものです。
しかしながら、これらは単純に足すことができず、抵抗\(R\)を実軸、リアクタンス\(X\)を虚軸においた複素平面で表されます。
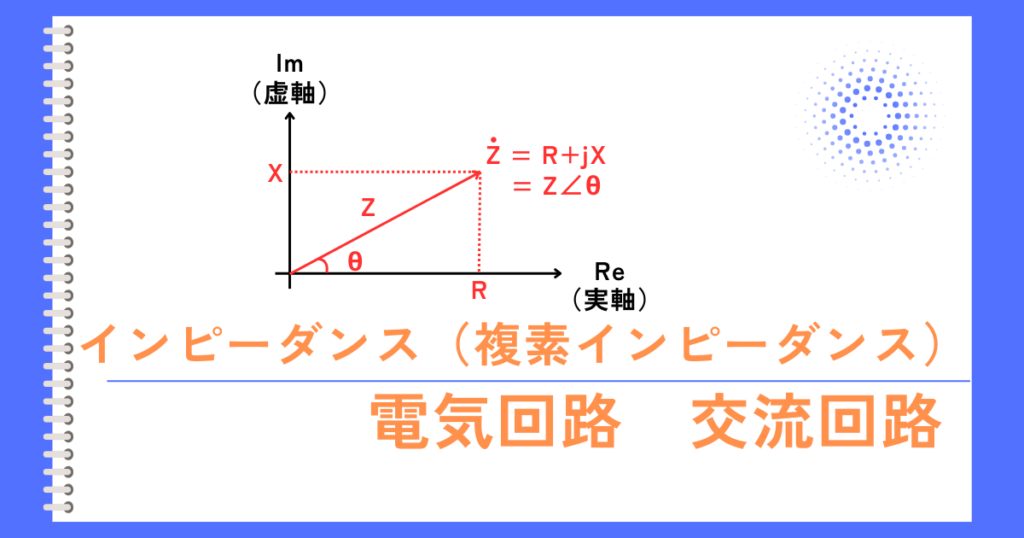
複素数を使って表したインピーダンスを複素インピーダンス\(\dot{Z}\)と呼び、次式で表されます。
\(\dot{Z}=R+jX\)
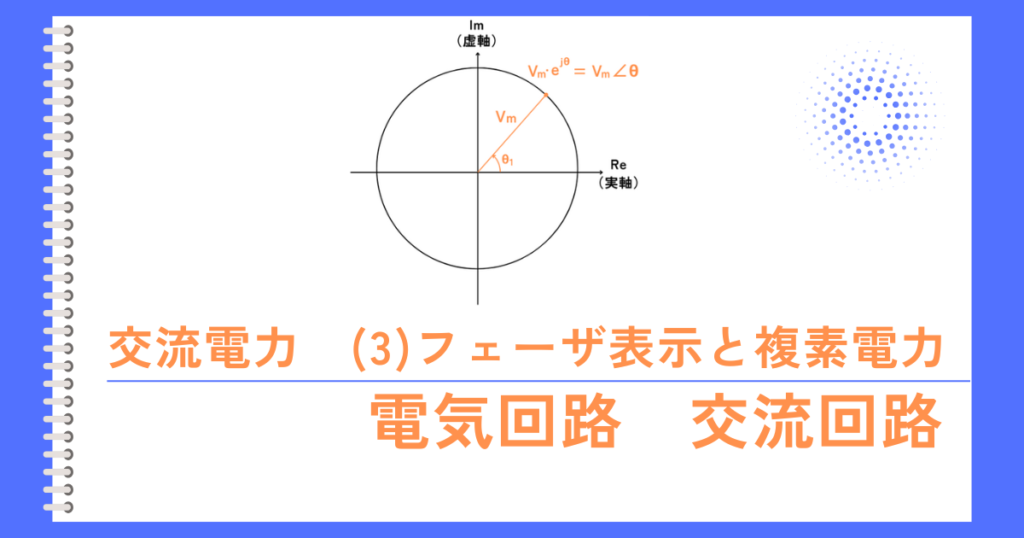
これを複素数平面上に表すと左図のようになります。
インピーダンスの大きさ\(Z\)は、直角三角形の斜辺の長さを求めればよいので、三平方の定理から、次式で表されます。
\(Z=\sqrt{R^2+X^2}\)
インピーダンスの位相角\(θ\)は、インピーダンス\(Z\)と実軸(抵抗\(R\))のなす角の事です。
この角度は、実軸\(R\)と、虚軸\(X\)の傾きなので、次のように求まります。
\(tanθ=\frac{X}{R}\)
⇔\(θ=tan^{-1}\frac{X}{R}\)
複素インピーダンスのフェーザ表示(極座標系)

頭にドットを付けることで、複素インピーダンス\(\dot{Z}\)と、インピーダンス\(Z\)の大きさを明確に区別します。
インピーダンスの大きさ\(Z\)と、位相角\(∠θ\)を使い、複素インピーダンス\(\dot{Z}\)を表す方法を、フェーザ表示と呼び、次のように表されます。
\(\dot{Z}=Z∠θ\)
フェーザ表示は、大きさと方向で成り立つベクトルに対して、
・大きさの計算
・方向の計算
を別々に計算してから、最終的にベクトルを導き出すことができるため計算がしやすいです。
そのため、交流回路の電流・電圧等を解析する際は、フェーザ表示を使用して解答することが必須といって良い程重要です。
直交座標系から、フェーザ表示への変換
複素インピーダンスを直交座標系で示すと、\(\dot{Z}=R+jX\) …①
RとXを極座標で示すと、\(R=Zcosθ\)、\(X=Zsinθ\) …②
①式に②式を代入すると、\(\dot{Z}=Z(cosθ+jsinθ)\) …③
③式にオイラーの公式を使うと、\(\dot{Z}=Ze^{jθ}\) …④
\(e^{jθ}\)を、\(∠θ\)として表すと、\(\dot{Z}=Z∠θ\)
以上より、直交座標系\(\dot{Z}=R+jX\)から、フェーザ表示\(\dot{Z}=Z∠θ\)に変換できました。
複素インピーダンスの計算
\(\dot{Z_1}=R_1+jX_1\)、\(\dot{Z_2}=R_2+jX_2\)の二つの複素インピーダンスがあったとします。このときの、インピーダンスの四則演算は次の通りになります。
加算\(\dot{Z}_{add}\)
\(\dot{Z}_{add}=\dot{Z_1}+\dot{Z_2}=(R_1+R_2)+j(X_1+X_2)\)
大きさ\(Z_{add}=\sqrt{(R_1+R_2)^2+(X_1+X_2)^2}\)
位相角\(θ_{add}=tan^{-1}\frac{X_1+X_2}{R_1+R_2}\)
減算\(\dot{Z}_{sub}\)
\(\dot{Z}_{sub}=\dot{Z_1}-\dot{Z_2}=(R_1-R_2)+j(X_1-X_2)\)
大きさ\(Z_{sub}=\sqrt{(R_1-R_2)^2+(X_1-X_2)^2}\)
位相角\(θ_{sub}=tan^{-1}\frac{X_1-X_2}{R_1-R_2}\)
乗算\(\dot{Z}_{mlt}\)
\(\dot{Z}_{mlt}=\dot{Z_1}・\dot{Z_2}=Z_1∠θ_1・Z_2∠θ_2=Z_1Z_2∠(θ_1+θ_2)\)
大きさ\(Z_{mlt}=Z_1Z_2\)
位相角\(θ_{mlt}=∠(θ_1+θ_2)\)
除算\(\dot{Z}_{div}\)
\(\dot{Z}_{div}=\frac{\dot{Z_1}}{\dot{Z_2}}=\frac{Z_1∠θ_1}{Z_2∠θ_2}=\frac{Z_1}{Z_2}∠(θ_1-θ_2)\)
大きさ\(Z_{div}=\frac{Z_1}{Z_2}\)
位相角\(θ_{div}=∠(θ_1-θ_2)\)
回路例
R回路(抵抗のみ)
抵抗のみの回路のインピーダンス\(\dot{Z}\)は、次式で表されます。
\(\dot{Z}=R=R\)
上式において、実数項\(Re=R\)、虚数項\(Im=0\)となります。
インピーダンスの大きさ\(Z\)は、
\(Z=\sqrt{Re^2+Im^2}=R\)
インピーダンスの位相角\(∠θ\)は、
\(\displaystyle θ=tan^{-1}\frac{Im}{Re}=tan^{-1}\frac{0}{R}=tan^{-1}0=0°\)
R回路(例題)
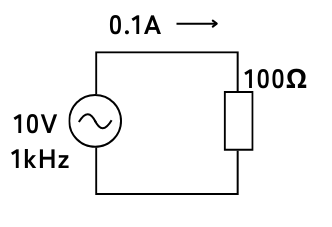
電圧\(v=10V\)、周波数\(1[kHz]\)の交流電圧源に、抵抗\(R=100Ω\)を接続したとき、交流回路に流れる電流\(i[A]\)ついて考えます。
複素インピーダンス\(\dot{Z}\)は、
\(Z=R=100\)
インピーダンスの大きさ\(Z\)は、
\(Z=\sqrt{100^2+0^2}=100\)
インピーダンスの位相角\(∠θ_Z\)は、
\(\displaystyle tanθ_Z=\frac{0}{R}=0\)
⇔ \(\displaystyle θ_Z=tan^{-1} 0=0 ° \)
以上より、複素インピーダンス\(\dot{Z}\)をフェーザ表示をすると、
\(\dot{Z}=100∠0°\)
電流\(i[A]\)の大きさは
\(\displaystyle I=\frac{v}{Z}=\frac{10}{100}=0.1A\)
電流\(i[A]\)の位相は、
\(\displaystyle ∠θ_i=\frac{∠θ_v}{∠θ_Z}=\frac{∠0°}{∠0°}=∠0°\)
以上より、電流\(i\)の大きさは0.1Aで、電圧\(v\)に対して位相が60°遅れていることが導き出せます。
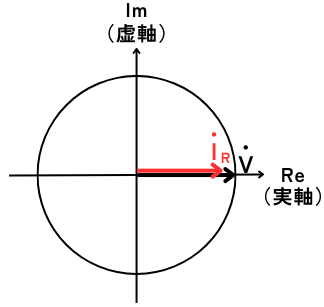
電圧、電流、インピーダンスの大きさと位相をまとめると、左図のようになります。
\(v=10∠0°\)
\(i=0.1∠0°\)
\(\dot{Z}=100∠0°\)
RL回路(直列接続)
RL回路のインピーダンス\(\dot{Z}\)は、次式で表されます。
\(\dot{Z}=R+jωL=R+j2πfL\)
上式において、実数項\(Re=R\)、虚数項\(Im=ωL=2πfL\)となります。
インピーダンスの大きさ\(Z\)は、
\(Z=\sqrt{Re^2+Im^2}=\sqrt{R^2+(ωL)^2}=\sqrt{R^2+(2πfL)^2}\)
インピーダンスの位相角\(∠θ\)は、
\(\displaystyle θ=tan^{-1}\frac{Im}{Re}=tan^{-1}\frac{ωL}{R}=tan^{-1}\frac{2πfL}{R}\)
RL回路(例題)
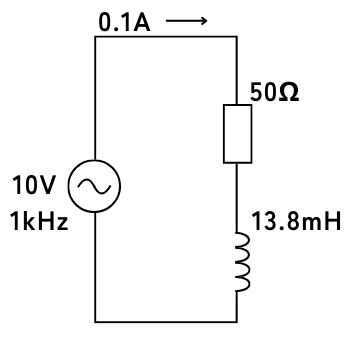
電圧\(v=10V\)、周波数\(1[kHz]\)の交流電圧源に、抵抗\(R=50Ω\)と、インダクタンス\(L=13.8mH\)のコイルを直列接続したとき、交流回路に流れる電流\(i[A]\)ついて考えます。
複素インピーダンス\(\dot{Z}\)は、
\(Z=R+j2πfL=50+j2π×10^3×13.8×10^{-3}\)
\(Z≒50+j86.6Ω\)
インピーダンスの大きさ\(Z\)は、三平方の定理を使い、
\(Z=\sqrt{50^2+86.6^2}≒100\)
インピーダンスの位相角\(∠θ_Z\)は、
\(\displaystyle tanθ_Z=\frac{X_L}{R}=\frac{86.6}{50}≒1.732\)
⇔ \(\displaystyle θ_Z=tan^{-1} \frac{X_L}{R}=tan^{-1}1.732=60 ° \)
以上より、複素インピーダンス\(\dot{Z}\)をフェーザ表示をすると、
\(\dot{Z}=100∠60°\)
電流\(i[A]\)の大きさは
\(\displaystyle I=\frac{v}{Z}=\frac{10}{100}=0.1A\)
電流\(i[A]\)の位相は、
\(\displaystyle ∠θ_i=\frac{∠θ_v}{∠θ_Z}=\frac{∠0°}{∠60°}=∠-60°\)
以上より、電流\(i\)の大きさは0.1Aで、電圧\(v\)に対して位相が60°遅れていることが導き出せます。
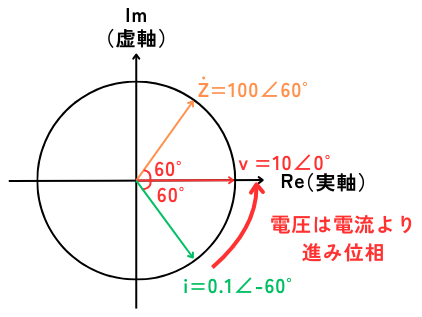
電圧、電流、インピーダンスの大きさと位相をまとめると、左図のようになります。
\(v=10∠0°\)
\(i=0.1∠-60°\)
\(\dot{Z}=100∠60°\)
RC回路(直列接続)
RC回路のインピーダンス\(\dot{Z}\)は、次式で表されます。
\(\displaystyle \dot{Z}=R+\frac{1}{jωC}=R-j\frac{1}{ωC}=R-j\frac{1}{2πfC}\)
上式において、実数項\(Re=R\)、
虚数項\(Im=-\frac{1}{ωC}=-\frac{1}{2πfC}\)となります。
インピーダンスの大きさ\(Z\)は、
\(\displaystyle Z=\sqrt{Re^2+Im^2}=\sqrt{R^2+(\frac{1}{ωC})^2}=\sqrt{R^2+(\frac{1}{2πfC})^2}\)
インピーダンスの位相角\(∠θ\)は、
⇔ \(\displaystyle θ=tan^{-1}\frac{Im}{Re}=tan^{-1}\frac{-1}{ωCR}=tan^{-1}\frac{-1}{2πfCR}\)
RC回路(例題)
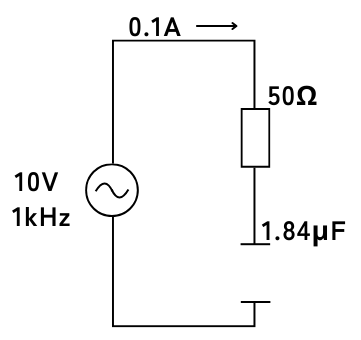
電圧\(v=10V\)、周波数\(1[kHz]\)の交流電圧源に、抵抗\(R=50Ω\)と、静電容量\(C=1.84μF\)のコンデンサを直列接続したとき、交流回路に流れる電流\(i[A]\)ついて考えます。
複素インピーダンス\(\dot{Z}\)は、
\(\displaystyle Z=R+\frac{1}{j2πfC}=R-j\frac{1}{2πfC}\)
\(\displaystyle Z=50-j\frac{1}{2π×10^3×1.84×10^{-6}}\)
\(\displaystyle Z≒50-j86.6\)
インピーダンスの大きさ\(Z\)は、三平方の定理を使い、
\(Z=\sqrt{50^2+86.6^2}=100\)
インピーダンスの位相角\(∠θ_Z\)は、
\(\displaystyle tanθ=\frac{X_C}{R}=\frac{-86.6}{50}=-1.732\)
⇔ \(\displaystyle θ_Z=tan^{-1} \frac{X_C}{R}=tan^{-1}-1.732=-60 ° \)
以上より、複素インピーダンス\(\dot{Z}\)をフェーザ表示をすると、
\(\dot{Z}=100∠-60°\)
電流\(i[A]\)の大きさは
\(\displaystyle I=\frac{v}{Z}=\frac{10}{100}=0.1A\)
電流\(i[A]\)の位相は、
\(\displaystyle ∠θ_i=\frac{∠θ_v}{∠θ_Z}=\frac{∠0°}{∠-60°}=∠60°\)
以上より、電流\(i\)の大きさは0.1Aで、電圧\(v\)に対して位相が60°進んでいる。
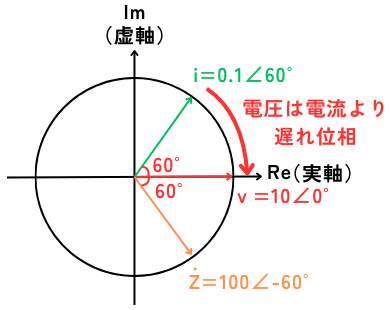
電圧、電流、インピーダンスの大きさと位相をまとめると、左図のようになります。
\(v=10∠0°\)
\(i=0.1∠60°\)
\(\dot{Z}=100∠-60°\)
RLC直列回路
RLC直列回路のインピーダンス\(\dot{Z}\)は、次式で表されます。
\(\displaystyle \dot{Z}=R+jωL+\frac{1}{jωC}\)
インピーダンスの大きさ\(Z\)と、インピーダンスの位相角\(∠θ\)は、複素数計算した後、実数項\(Re\)と、虚数項\(Im\)を次式の通り計算することで算出できます。
\(Z=\sqrt{Re^2+Im^2}\)
\(\displaystyle ∠θ=\tan^{-1}\frac{Im}{Re}\)
RLC直列回路(例題)
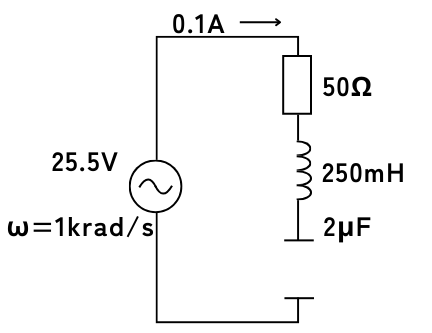
電圧\(v=25.5V\)、角周波数\(ω=1[krad/s]\)の交流電圧源に、抵抗\(R=50Ω\)と、インダクタンス\(250mH\)のコイル、静電容量\(C=2μF\)のコンデンサを直列接続したとき、交流回路に流れる電流\(i[A]\)ついて考えます。
複素インピーダンス\(\dot{Z}\)は、
\(\displaystyle Z=R+jωL+\frac{1}{jωC}=R-j\frac{1-ω^2LC}{ωC}\)
\(\displaystyle Z=50-j\frac{1-(10^3)^2×250×10^{-3}×2×10^{-6}}{10^3×2×10^{-6}}\)
\(\displaystyle Z≒50-j250\)
インピーダンスの大きさ\(Z\)は、三平方の定理を使い、
\(Z=\sqrt{50^2+250^2}=255Ω\) と求まります。
インピーダンスの位相角\(∠θ_Z\)を求めます。
\(Z≒50-j250\)から、実数項は\(Re=50\)、虚数項は\(Im=-250\)となります。
\(\displaystyle tanθ=\frac{Im}{Re}=\frac{-250}{50}=-5\)
⇔ \(\displaystyle θ_Z=tan^{-1} -5≒-78.7° \)
以上より、複素インピーダンス\(\dot{Z}\)をフェーザ表示をすると、
\(\dot{Z}=255∠-78.7°\)
電流\(i[A]\)の大きさは
\(\displaystyle I=\frac{v}{Z}=\frac{25.5}{255}=0.1A\)
電流\(i[A]\)の位相は、
\(\displaystyle ∠θ_i=\frac{∠θ_v}{∠θ_Z}=\frac{∠0°}{∠-78.7°}=∠78.7°\)
以上より、電流\(i\)の大きさは0.1Aで、電圧\(v\)に対して位相が78.7°進んでいる。
RLC並列回路
RLC並列回路のインピーダンス\(\dot{Z}\)は、次式で表されます。
\(\displaystyle \frac{1}{\dot{Z}}=\frac{1}{R}+\frac{1}{jωL}+\frac{1}{\frac{1}{jωC}}\)
インピーダンスの大きさ\(Z\)と、インピーダンスの位相角\(∠θ\)は、複素数計算した後、実数項\(Re\)と、虚数項\(Im\)を次式の通り計算することで算出できます。
\(Z=\sqrt{Re^2+Im^2}\)
\(\displaystyle ∠θ=\tan^{-1}\frac{Im}{Re}\)
RLC並列回路(例題)
\(1V\)で角周波数\(ω[krad/s]\)が変化する正弦波交流電源を含む回路とし、下図のようなRLC並列接続回路において、\(ω\)の値が\(ω=5krad/s\)のときの電流\(i\)について考えます。
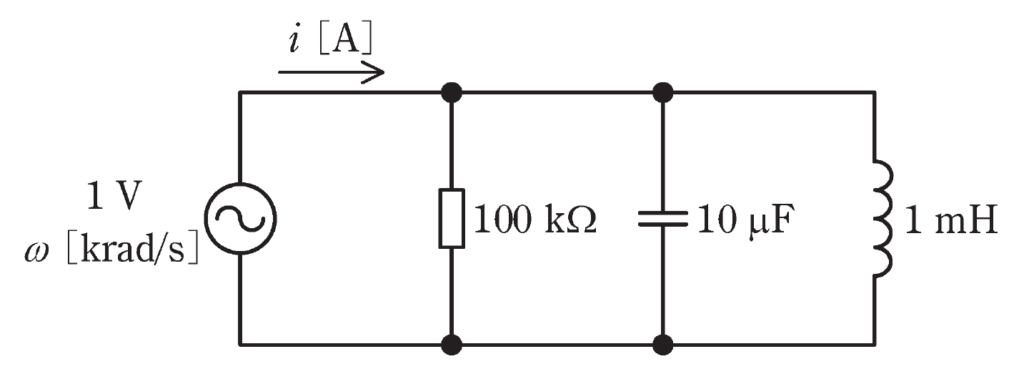
並列接続時のインピーダンスは、並列抵抗の合成抵抗を求める時と同様に、逆数を足し合わせることで求めることが出来ます。
\(\displaystyle \frac{1}{Z}=\frac{1}{R}+\frac{1}{\frac{1}{jωc}}+\frac{1}{jωL}\)
⇔ \(\displaystyle \frac{1}{Z}=\frac{1}{R}+jωC+\frac{1}{jωL}\)
⇔ \(\displaystyle \frac{1}{Z}=\frac{1}{R}+j \frac{ω^2LC-1}{ωL}\)
\(ω_1=5krad/s=5×10^3rad/s\)をすると、
・\(R=100kΩ=10^5Ω\)
・\(ωC=(5×10^3)×(10×10^{-6})=5^{-2}=0.05Ω\)
・\(ωL=(5×10^3)×(1×10^{-3})=5Ω\)
⇒\(ω^2LC=0.05×5=0.25\)
\(\displaystyle \frac{1}{Z}=\frac{1}{10^5}+j \frac{0.25-1}{5}=10^{-5}-j 0.15\)
オームの法則から、\(i\)を求める。
\(\displaystyle i=\frac{V}{Z}=\frac{1}{Z}=10^{-5}-j 0.15\)
電流\(i[A]\)の大きさ\(I[A]\)は
\(I=\sqrt{(10^{-5})^2+0.15^2}≒0.15A\)
電流\(i[A]\)の位相\(∠θ°\)を求めます。
\(i=10^{-5}-j 0.15\)の計算結果から、実数項は\(Re=10^{-5}\)、虚数項は\(Im=-0.15\)となります。
\(\displaystyle tanθ=\frac{Im}{Re}=\frac{-0.15}{10^{-5}}=-15000\)
⇔ \(\displaystyle θ=tan^{-1} -15000≒-90 ° \)
以上より、電流\(i\)の大きさは0.15Aで、電圧\(v\)に対して位相が90°遅れている。
虚数単位\(j\)
高校数学では虚数単位を\(i\)としますが、電気数学では虚数単位を\(j\)とします。
これは、ローマ字の\(i\)は、電気工学では電流\(i\)として使用することが多く、混同しやすいため、それを避けるために\(j\)を使用します。
虚数単位は次式で表されます。
\(j=\sqrt{-1}\)
\(j^2=-1\)
関連記事(交流回路に関する解説)
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント