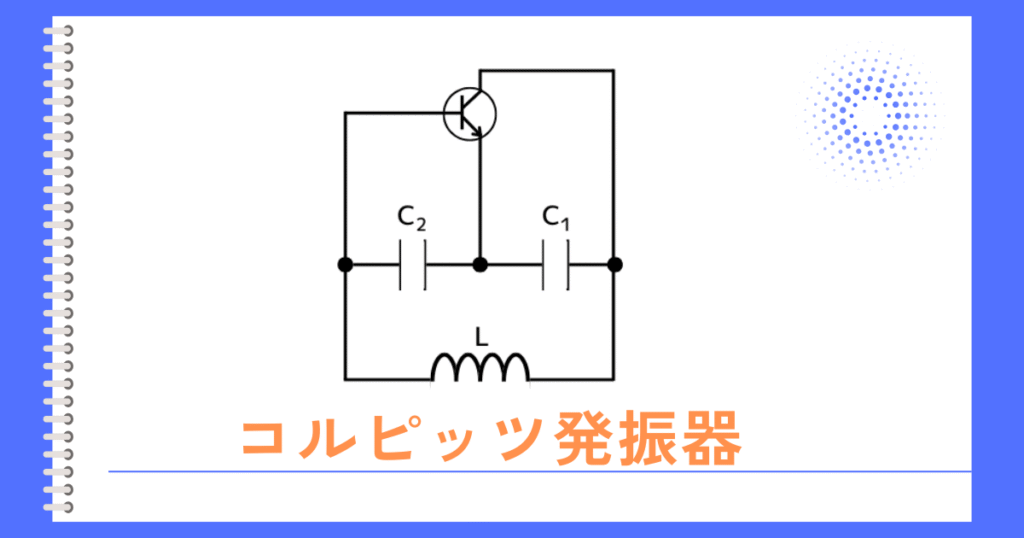
コルピッツ発振器とは
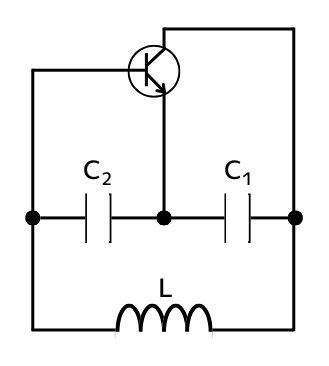
コルピッツ発振器は、トランジスタ、2個のコンデンサ、コイルで作れる発振回路です。
発振とは、電気に限らず、特定の周波数で持続的に振動を発生させることです。特に、外部からの入力が無くても、振動が継続することが重要です。
発振回路は、増幅回路を正帰還することで発振させます。そのことにより、特定の正弦波等の電気的振動を出力する回路です。
コルピッツ発振回路は、高い周波数で発振させることができるため、ラジオの受信機等に使用されます。
発振条件
ループ利得\(AH\)が次の2つの条件を満たすことが発振条件です。
振幅条件:\(Re(AH)>1\)
周波数条件:\(Im(AH)=0\)
振幅条件について
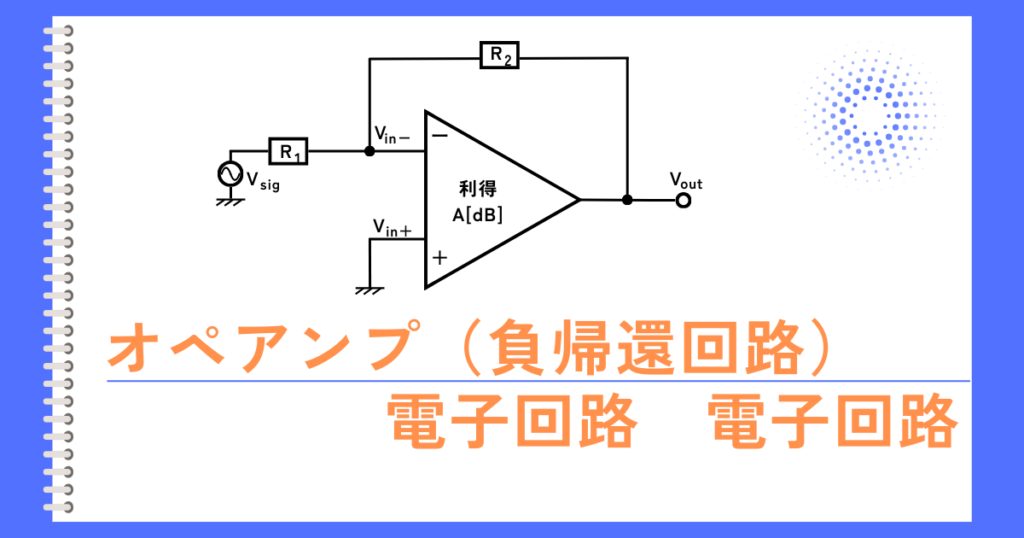
次のような、オペアンプの正帰還回路を考えます。
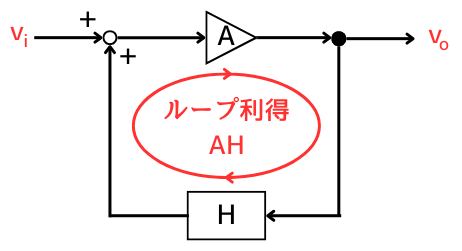
\(A\)はオペアンプの電圧利得で、\(H\)は帰還率です。
出力\(v_o\)が帰還率\(H\)倍した後、オペアンプで\(A\)倍されて帰ってくると、\(v_o\)は\(AH\)倍されます。
この\(AH\)は帰還回路を一巡したときの利得であり、ループ利得と呼びます。
ループ利得\(AH=1\)のとき、出力電圧\(v_0\)が帰還して増幅された結果が1倍となるので、減衰も、増幅もしません。
ループ利得\(AH>1\)のとき、出力電圧\(v_0\)が帰還して増幅された結果が1倍よりも大きくなるので、増幅していきます。
出力電圧\(v_o\)は、飽和するまで増幅するため、\(AH≧1\)のときに発振します。
周波数条件について
\(Im(AH)\)は、ループ利得\(AH\)の虚数部分です。
ループ利得\(AH\)の虚数部分が0でないとき、つまり、\(Im(AH≠0)\)のときは、ループする信号の位相が位相差角分ずれていきます。
その結果、ループ信号は反転し、減衰させる方向に働いてしまうため、\(Im(AH≠0)\)のときは発振することが出来ません。
そのため、\(Im(AH=0)\)が発振条件となります。
コルピッツ発振器の回路解析
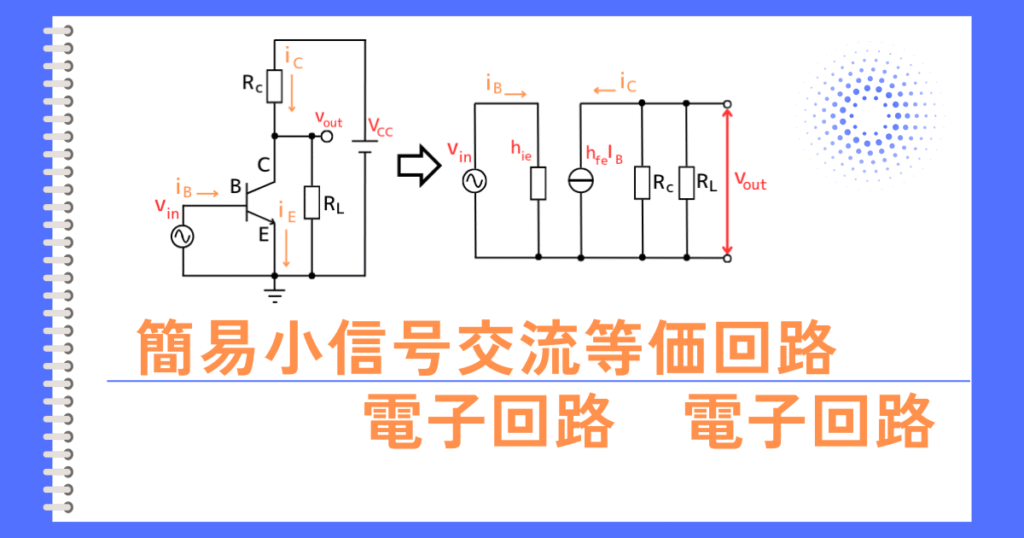
(1)簡易小信号等価回路に書変え
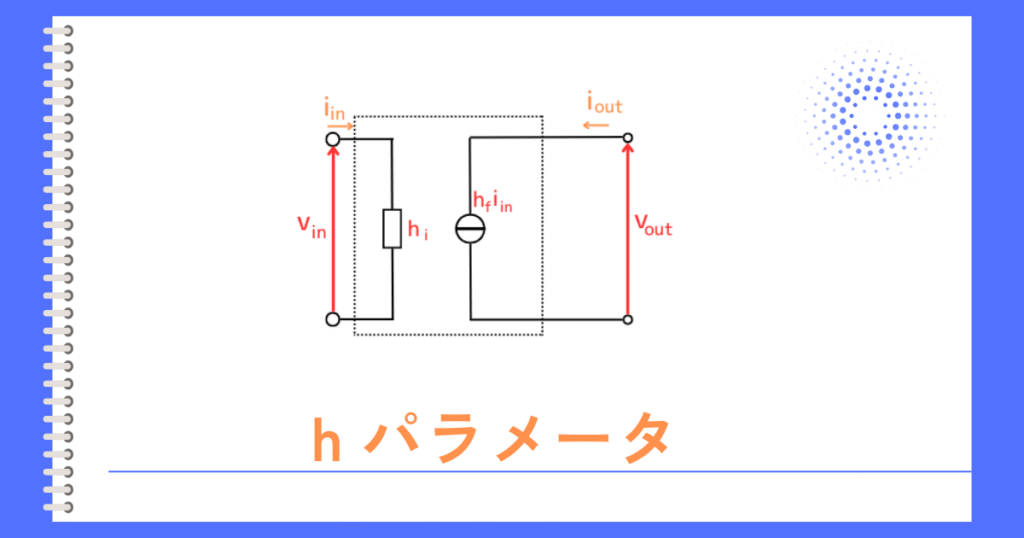
回路解析をするために、トランジスタを簡易小信号等価回路に書き変えます。
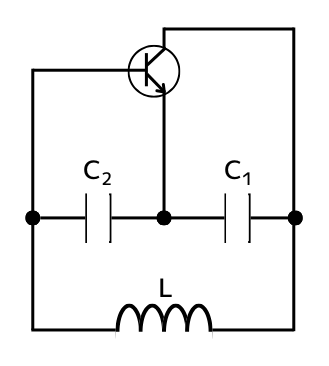
➡

回路中の各パラメータの意味は、次の通りです。
\(v_i\):入力電圧
\(v_o\):出力電圧
\(i_i\):入力電流
\(h_i\):入力インピーダンス
\(h_f\):電流増幅率
\(h_o\):出力アドミタンス
\(C_1\):コンデンサ
\(C_2\):コンデンサ
\(L\):リアクトル
(2)ループ利得の式を求める
入力電圧\(v_i\)と、入力電流\(i_i\)の関係は、
\(i_i=\frac{v_i}{h_i}\) …①
電流源から右側をみたアドミタンス\(Y_c\)は、
\(Y_c=\frac{1}{h_o}+jωC_1+\frac{1}{jωL+\frac{1}{jωC_2}}\) …②
電流源から右側をみたインピーダンス\(Z_c\)は、
\(Z_c=\frac{1}{Y_c}\) …③
コレクタの電圧\(v_c\)は、
\(\displaystyle v_c=-h_fi_iZ_c=\frac{-h_fi_i}{\frac{1}{h_o}+jωC_1+\frac{1}{jωL+\frac{1}{jωC_2}}}\) …④
出力電圧\(v_o\)は、分圧則から、
\(\begin{eqnarray}
v_o&=&\frac{\frac{1}{jωC_2}}{jωL+\frac{1}{jωC_2}}v_c \\
&=&\frac{\frac{1}{jωC_2}}{jωL+\frac{1}{jωC_2}}\frac{-h_f\frac{v_i}{h_i}}{\frac{1}{h_o}+jωC_1+\frac{1}{jωL+\frac{1}{jωC_2}}} …⑤
\end{eqnarray}\)
したがって、ループ利得\(AH\)は、次のように求まります。
\(\displaystyle AH=\frac{v_o}{v_i}=\frac{\frac{1}{ωC_2}}{ωL-\frac{1}{ωC_2}}\frac{\frac{h_f}{h_i}}{\frac{1}{h_o}+jωC_1+\frac{1}{jωL+\frac{1}{jωC_2}}}\) …⑥
(3)周波数条件:\(Im(AH)=0\)
⑥式の虚数項のみを取り出して展開していきます。
\(\displaystyle \begin{eqnarray}
Im(AH)&=&Im \left(\frac{v_o}{v_i} \right)=0 \\ \\
&⇔& jωC_1+\frac{1}{jωL+\frac{1}{jωC_2}}=0 \\ \\
&⇔& \frac{C_1}{C_2}+\frac{1}{1-ω^2LC_2}=0 \\ \\
&⇔& ω^2LC_1=1+\frac{C_1}{C_2} \\ \\
&⇔& ω^2=\frac{C_1+C_2}{LC_1C_2} \\ \\
&⇔& ω=\sqrt{\frac{C_1+C_2}{LC_1C_2}} …⑦
\end{eqnarray}\)
以上より、発振する角周波数 \(ω\) を求めることができました。
(4)振幅条件:\(Re(AH)≧1\)
⑥式の実数項のみを取り出して展開していきます。
\(\displaystyle Re(AH)=Re \left(\frac{v_o}{v_i} \right)=\frac{\frac{1}{ωC_2}}{ωL-\frac{1}{ωC_2}}\frac{\frac{h_f}{h_i}}{\frac{1}{h_o}}≧1\)
⇔ \(\displaystyle \frac{1}{ω^2LC_2-1}\frac{h_oh_f}{h_i}≧1\) …⑧
周波数条件で求めた⑦式の \(ω\) を代入し、式の整理をするため部分的な計算をします。
\(\displaystyle ω^2LC_2-1=\frac{C_1+C_2}{LC_1C_2}LC_2-1=\frac{C_2}{C_1}\) …⑨
⑧式に⑨式を代入すると、次のように振幅条件が求まります。
\(\displaystyle \frac{C_1}{C_2}\frac{h_oh_f}{h_i}≧1\)
(5)回路解析の結果まとめ
回路解析した結果、周波数条件、振幅条件を求めることが出来ました。
周波数条件
\(\displaystyle ω=2πf=\sqrt{\frac{C_1+C_2}{LC_1C_2}}\)
⇔ \(\displaystyle f=\frac{1}{2π}\sqrt{\frac{C_1+C_2}{LC_1C_2}}\)
振幅条件
\(\displaystyle \frac{C_1}{C_2}\frac{h_oh_f}{h_i}≧1\)
関連記事
参考書
イラストがとても多く、視覚的に理解しやすいので、初学者に、お勧めなテキストです。
問題のページよりも、解説のページ数が圧倒的に多い、初学者に向けの問題集です。
問題集は、解説の質がその価値を決めます。解説には分かりやすいイラストが多く、始めて電気に触れる人でも取り組みやすいことでしょう。
本ブログの管理人は、電験3種過去問マスタを使って電験3種を取りました。
この問題集の解説は、要点が端的にまとまっていて分かりやすいのでお勧めです。
ある程度学んで基礎がある人に向いています。


コメント